算法003：快乐数

这道题采用快慢双指针的方法。

为了弄清楚这个题到底是要我们干嘛，我们把整个过程类比一下：

不管是n=19还是n=2，我们都把它当成一种判断链表是否有环的方式。

对于n=19，题干是这样解释的：

我们把它当成链表，最后判断链表是否有环；在这个题里面，也就是判断最终的结果是否为1。

为什么能够这样判断呢？

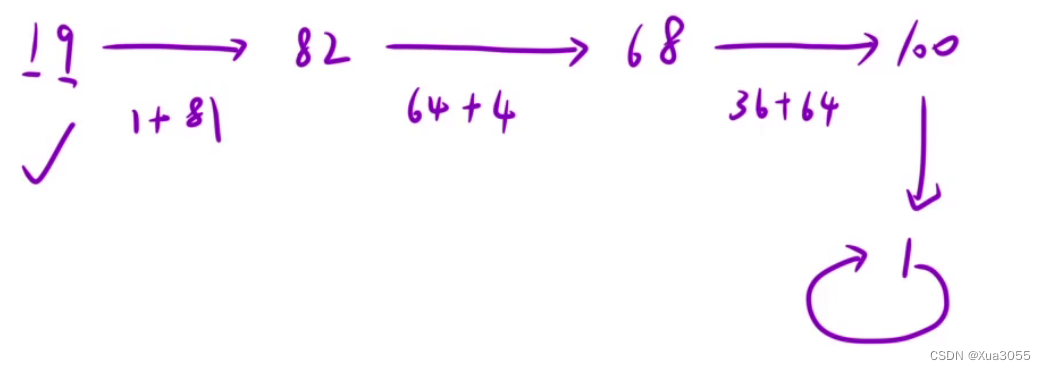
对于快乐数，一直到最后到1，我们可以看做最后进入了只有1的循环。

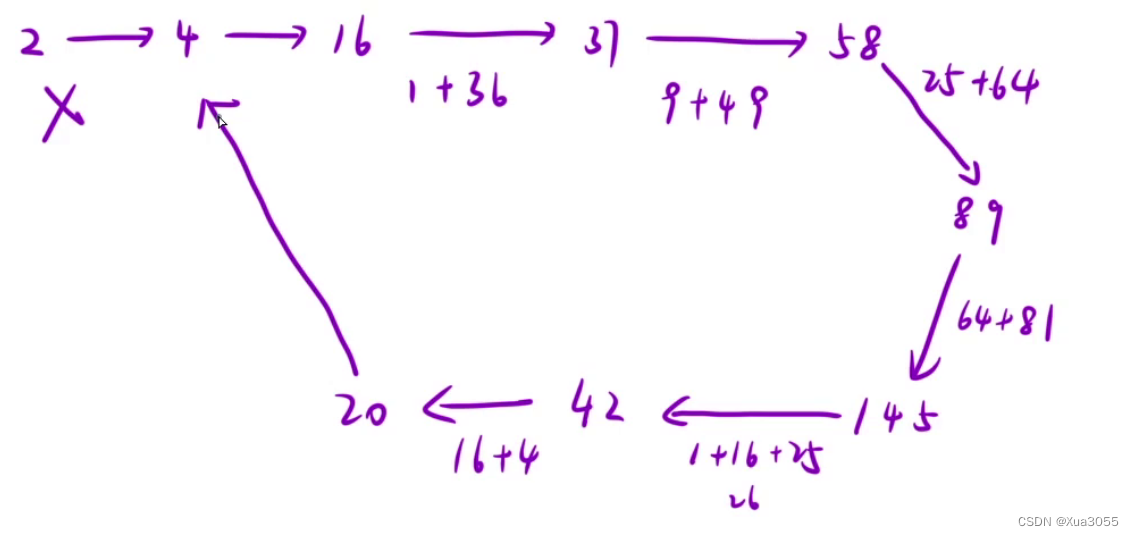
对于非快乐数，它们的平方和序列会进入一个固定的循环，例如4 → 16 → 37 → 58 → 89 → 145 → 42 → 20 → 4。

于是发现：只需要判断最终循环，结果是不是1就能够判断是不是快乐数。

这时候又会有另一个问题：如何知道我们判断的时候是因为 非快乐数不是1 而不是因为 快乐数还没有循环到一定的次数所以还没到1？

其实这就是为什么我们使用快慢双指针的原因了。只有已经进入了环，那么才会有慢指针追上快指针的那个时候，否则就会认为还没有进入循环，还有可能是在第一个循环中。

此时这个题的思路就明晰了，先规定两个指针，slow和fast，fast一次执行两次操作，slow一次执行一次操作，等到slow和fast相等的时候判断值是否为1。

代码就很好操作了，先把一次操作作为一个方法，只需要让fast和slow执行这个方法就行了。

（slow和fast初始化的时候不能相等，先让fast执行一次）

java 复制代码

class Solution {
    public int bitSum(int n){
        int sum = 0;
            while(n != 0){
                int t = n % 10;
                sum += t * t;
                n = n / 10;
            }
            return sum;
        }

    public boolean isHappy(int n) {
        int slow = n;
        int fast = bitSum(n);
        while(slow != fast){
            slow = bitSum(slow);
            fast = bitSum(bitSum(fast));
        }
        return slow == 1;
    }
}

tips：把快乐数的循环当成全都是1的循环。