前言
学习笔记，仅供学习，不做商用，如有侵权，联系我删除即可
一、目标
1.理解光流法跟踪特征点的原理。
2.理解直接法是如何估计相机位姿的。
3.实现多层直接法的计算。
特征点法存在缺陷：
二、光流(Optical Flow)
光流：空间运动物体在观察成像平面上的像素运动的瞬时速度。
稀疏光流：计算部分像素的运动
稠密光流：计算所有像素的运动
Lucas-Kanade光流
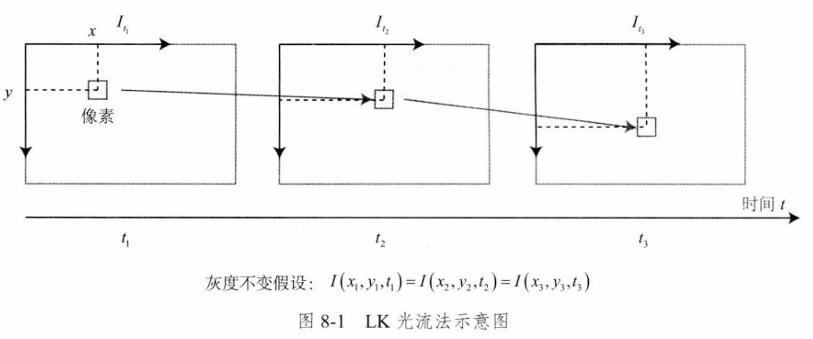
灰度不变假设：同一个空间点的像素灰度值，在各个图像中是固定不变的。灰度不变假设是一个很强的假设，实际中很可能不成立。
根据灰度不变假设，有：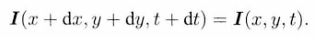
于是有：
在LK光流中，假设某一个窗口(patch)内的像素具有相同的运动。
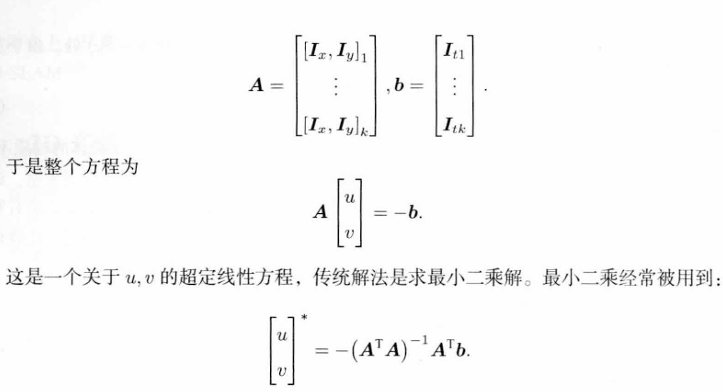
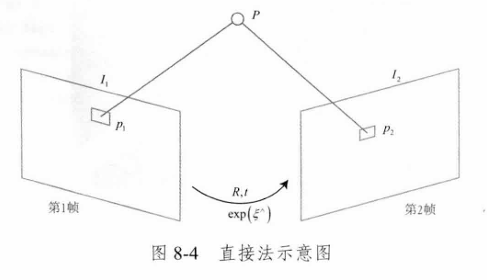
三、直接法
依旧是灰度不变假设的前提，同时还需要无遮挡，完全漫发射，不考虑光照变化的前提
目标函数：最小化光度误差（Photometric error）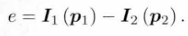
直接法的跟踪方式有：LSD，SVO，DTAM等开源方案。
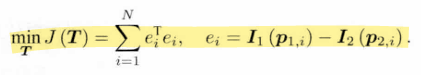，第一项与相机位姿没有关系，所以只对第二项求梯度，因此引入中间变量：，所以会有：
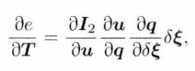
第一项：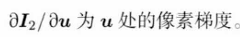
，像素点位置变化时，图像亮度的变化情况。
第二项：空间点的变化对像素坐标的影响。
第三项：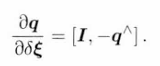
后两项只与三维点q有关，与图像无关，因此常合到一起，物理意义为：相机发生微小运动后，投影在像面上的像素点位置的变化情况，**也就是重投影误差的梯度，**其公式形式为：
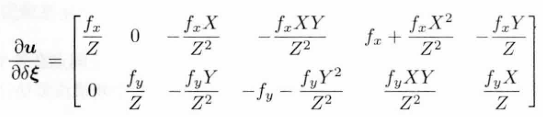
DTAM------使用所有像素。（但无梯度处对目标函数无贡献）
SVO------使用fast关键点处所在的4x4的patch。（fast特征点表明该处梯度明显）
LSD------使用梯度明显的所有像素点。（数量比SVO多，但比所有像素要少）
非线性优化的实现方式：
Eigen：需要自己编写，优点是中间过程可以检验是否正确
g2o：快速且方便，但中间过程被隐藏在中间框架里，不可视
直接法的优点：
-
可以省去计算特征点、描述子的时间。
-
只要求有像素梯度即可，不需要特征点。因此，直接法可以在特征缺失的场合下使用。比较极端的例子是只有渐变的一幅图像。它可能无法提取角点类特征，但可以用直接法估计它的运动。在演示实验中，我们看到直接法对随机选取的点亦能正常工作。这一点在实用中非常关键，因为实用场景很有可能没有很多角点可供使用。
-
可以构建半稠密乃至稠密的地图，这是特征点法无法做到的。
直接法的缺点：
-
非凸性！直接法完全依靠梯度搜索，降低目标函数来计算相机位姿。 但是图像本身是强烈非凸的函数。------优化算法容易局部极小，只在运动很小时才行。
-
单个像素没有区分度。找一个和它像的实在太多了！------每个像素对改变相机运动的"意见"不一致。只能少数服从多数，以数量代替 质量。
-
灰度值不变是很强的假设。
直接法适用于初始值还不错，而且前后两帧的运动距离不能差太远的情况。
总结
