承接上文我们讲完了页式管理和段式管理,接下来让我们深入讲解一下快表和二级页表
快表
快表和计算机组成原理讲的Cache原理如出一辙。为了减少访存的次数,OS在访问页面的时候创建了快表(Translation Lookaside Buffer ,简称TLB),包含最近使用过的页表表项,避免了反复查询处于内存中的页表。
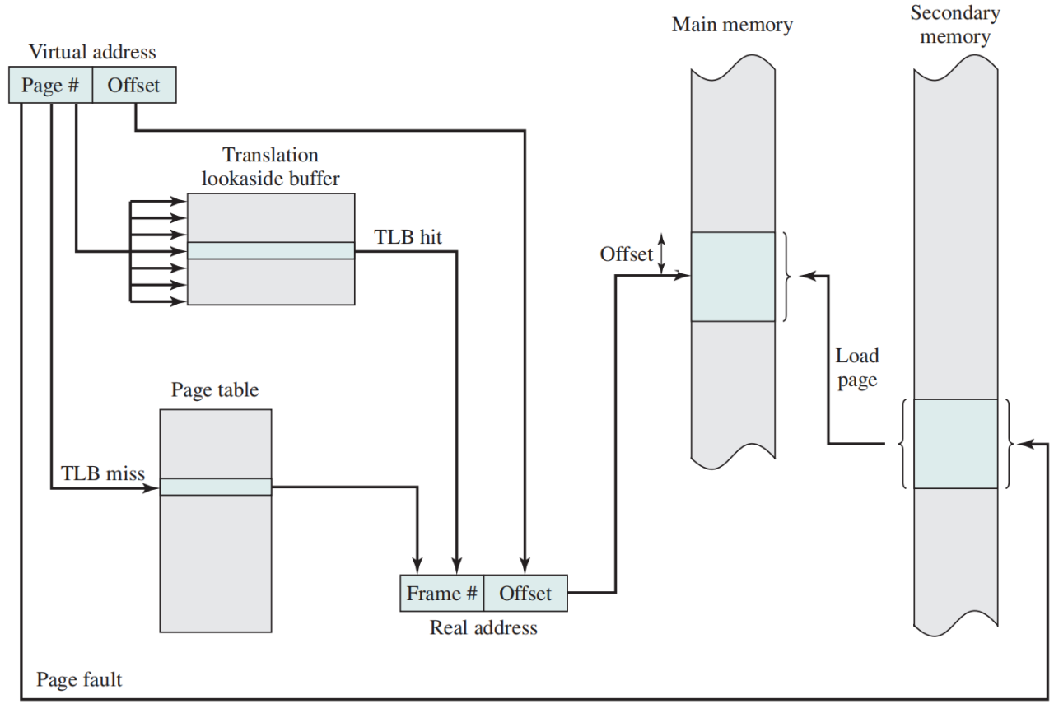
如图所示,OS会先根据TLB是否命中决定是否访问在内存中的页表,如果命中就直接拿着快表表项组合已有的偏移量构成物理地址。反之,OS会继续访问页表找到对应的页表项,得到物理地址,然后将该页表项加入到快表中以备下次查询。如果快表和页表都没有找到,就会引发缺页中断,有关内容我们下一章节会详细叙述。
二级页表
首先,我们先思考一个问题,假设的是32位逻辑地址,页面大小为4kb,并且假设页表项大小为4B,那么一个进程最多有多少页,需要分配的页框占据多少空间?
页面大小是4KB,也就是需要12位表示业内偏移量,总共有32位逻辑地址,剩余20位组成页号,也就是一个进程最多有220个页,每个页对应一个页号,而一个页号对应一个页表项,则至少需要220 *4 = 2^22个字节的空间存放,即4GB的空间。
实际上,我们普通电脑的内存不过8GB、16GB,如果光是一个进程就干掉4GB,那显然是捉襟见肘的。同时,由于一个进程的页面是连续存放的,那么一个进程就要连续分配4GB/4Kb = 1024个页面,显然一次性给一个进程分配这么多页面也是不合理的。
实际上,进程不会一次访问所有的页面,而是只会访问特定的页面,所以我们不需要一次性分配所有的页面。为了解决进程页面必须连续存放的问题,我们采用解决进程在内存中连续存放的思路,使用二级页表,把页面存放离散化。
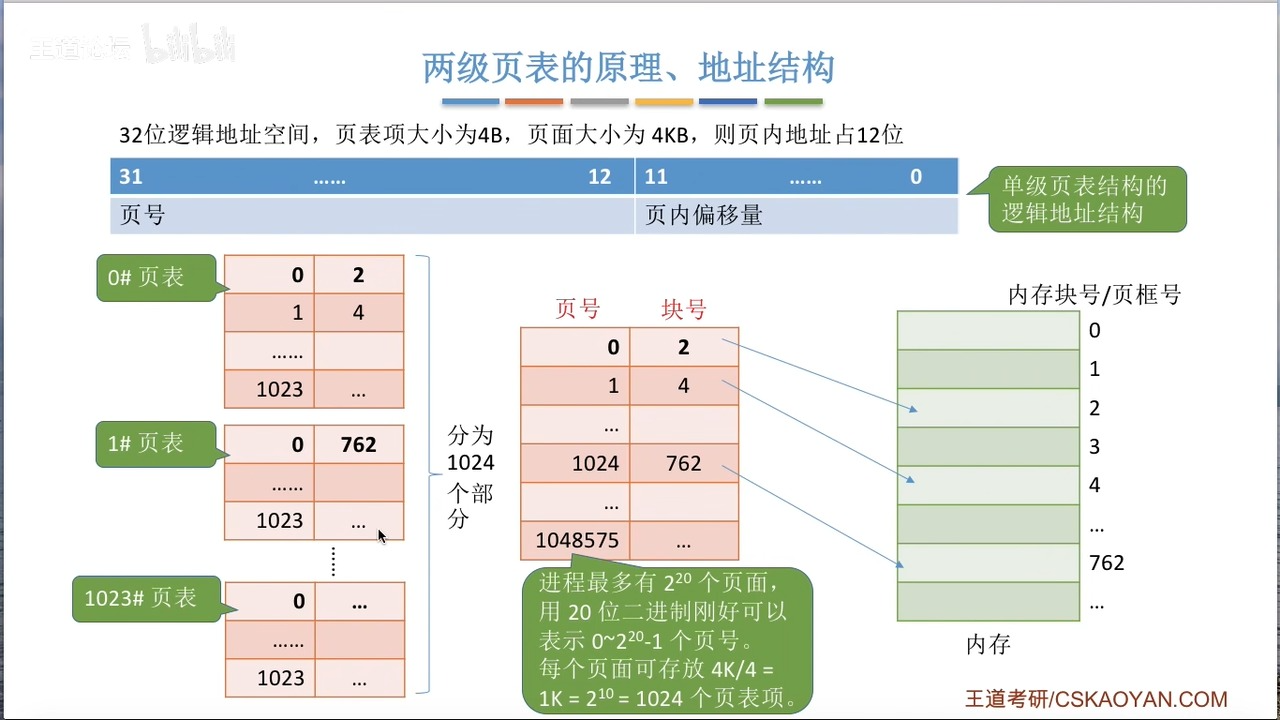
如图所示,我们已知页表是一种索引结构,进程有2^20个页也就是有0~1048575的页号,我们在此基础上分组,每1024个为一组,总共就是1024组,然后在每一组中的页号对1024取余,统一成0~1023。然后再在这1024组上建一层索引,也就构成了我们的页目录。
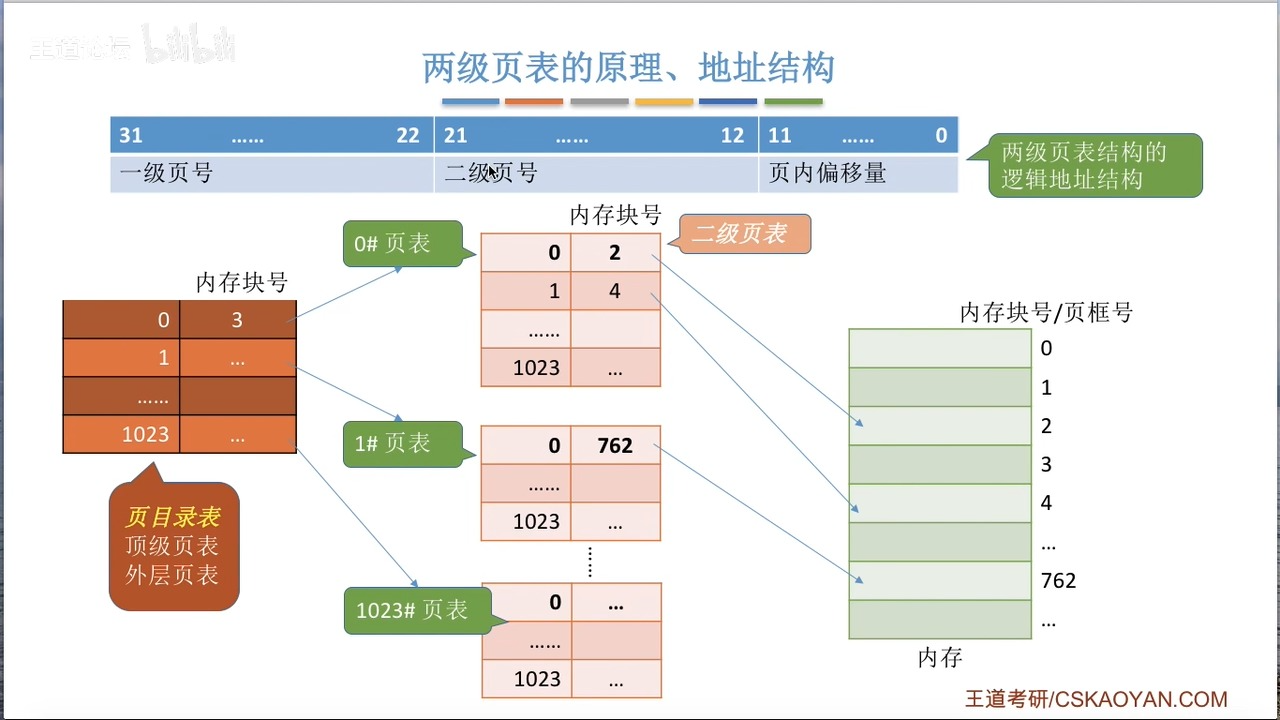
奇妙的是,按照1024划分,每一个二级页表刚好对应一个页框,而页目录表也是一个页框(1024*4B = 4KB)。也就是说,我们将原先连续的页面按照页框大小分组,然后在分组上建索引得到了一个新的页表------页目录表。
现在,我们查询就要分为两次:先查页目录表,对应的内存块号是存二级页表的内存位置,然后再查二级页表,二级页表中的内存块号就是实际访存的内存块号了。
与之对应,二级页表的逻辑地址结构部分,原先的前20位页号就要拆成一级页号和二级页号。
其中,查页目录表就是查一级页号对应的内存块号,然后根据该内存块号找到内存中对应的二级页表,然后根据二级页号查二级页表找到对应的内存块号,就是实际访存的内存块。
而一级页号总共是10位,因为总共有1024个二级页表,二级页号也有10位,因为每个二级页表有1024个页表项。
建立多级页表本质上就是建立多重索引。二级页表就是借助二重索引的迭代查询来实现对于一重索引的离散化。
举一个更具体的例子
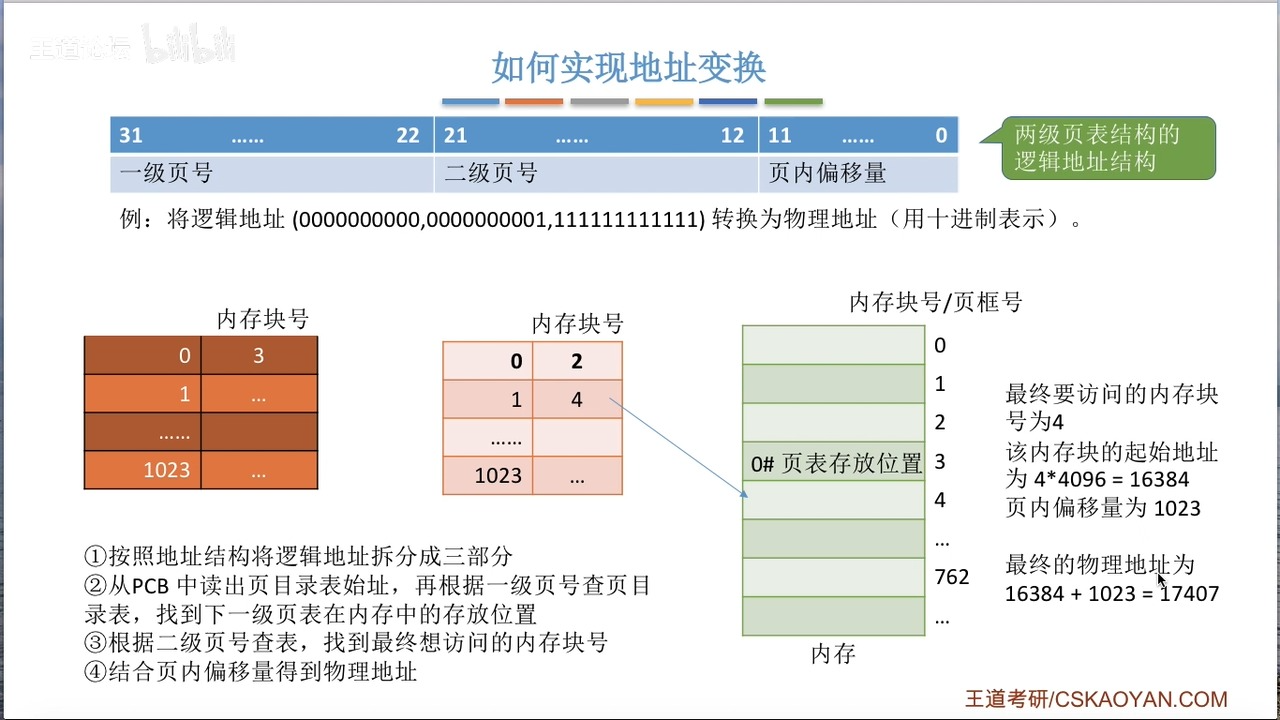
假设我们的32位的逻辑地址如图所示,根据10+10+12的原则,一级页号就是0,二级页号就是1,页内偏移就是1023.
我们先在页目录表中查一级页号对应的内存块号3,再到与之对应的二级页表中查询二级页号1,得知内存块号4是最终需要访问的内存块,结合页面大小4KB,最终的访问地址是4*4K+1023 = 17407。
几个细节
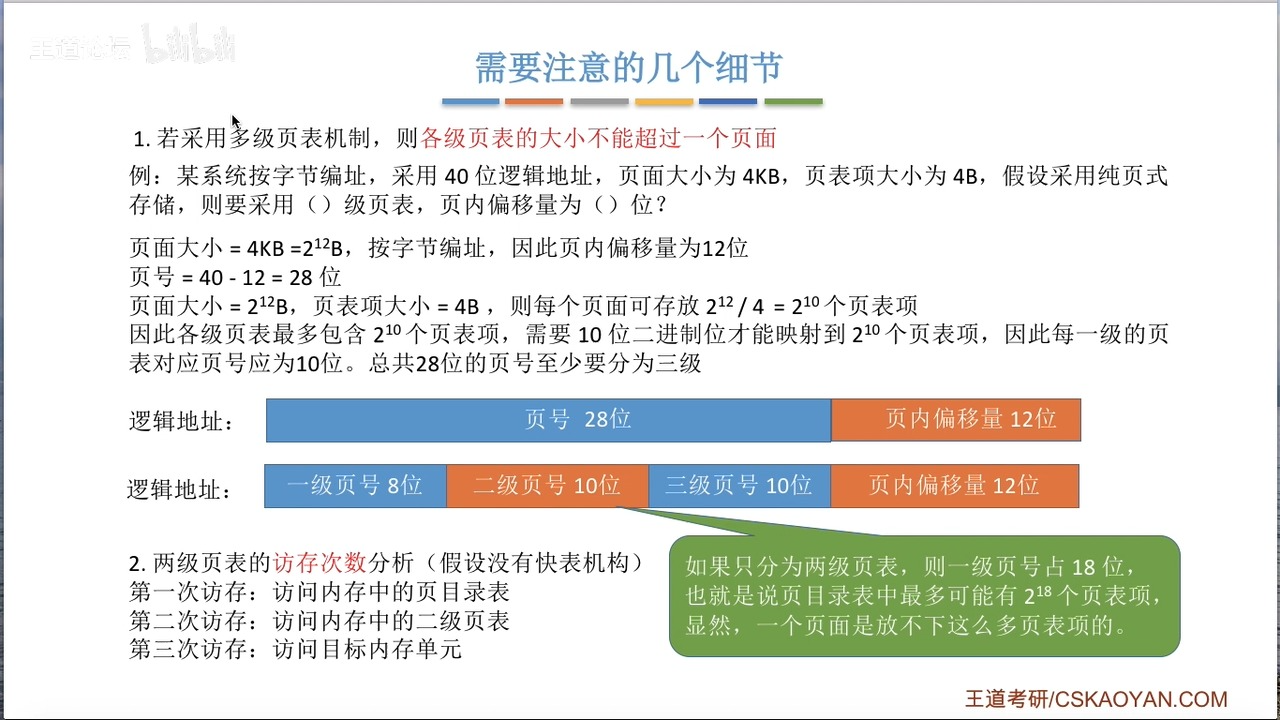
一般来说,各级页表大小不能超过一个页面,不然就又会出现页面连续存放的问题。
所以上述例子中,每级页表最多2^10个,占用10位,40位逻辑地址就至少需要三级页表,即(40-12)/ 3 向上取整。
假设不考虑TLB,访存次数根据页表级数N而定,因为页表也是存储在内存中的,所以查询每一级页表都需要访存,最终访存次数是N+1。
至于一开始提到的进程自身页表存储量最高可达4GB,现有的内存容量无法满足需求的解决方案,我们将会在下一章的虚拟存储中提及。