1. 决策树与熵
1.1 决策树简介
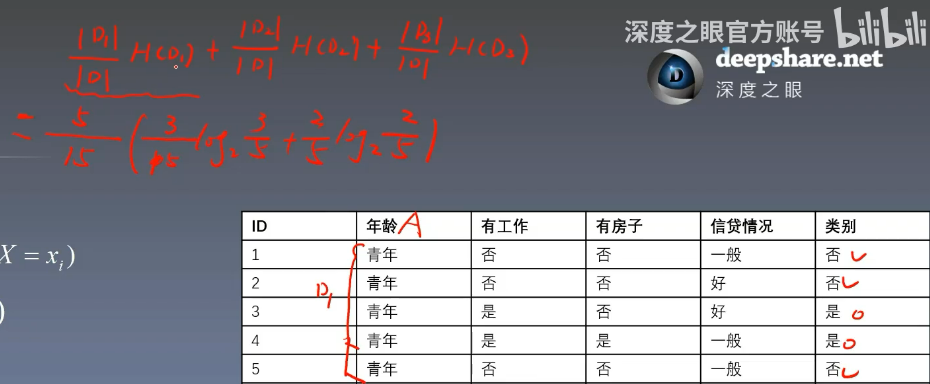
- 下面有一个贷申请样本表,有许多特征
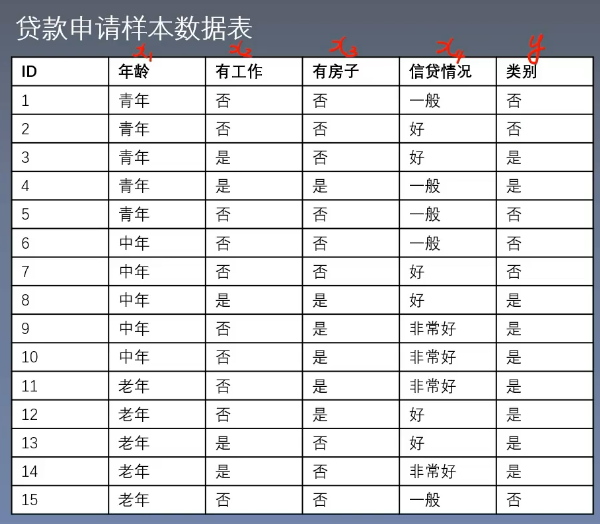
- 我们根据特征数据生成一棵树,比如年龄有青年,中年,老年三个类别,那么就有三个分支,分别对应着三种类别。如果是青年那么就看工作,如果有工作就给他贷款,如果没工作就不给他贷款。以上面这个例子来理解这棵树
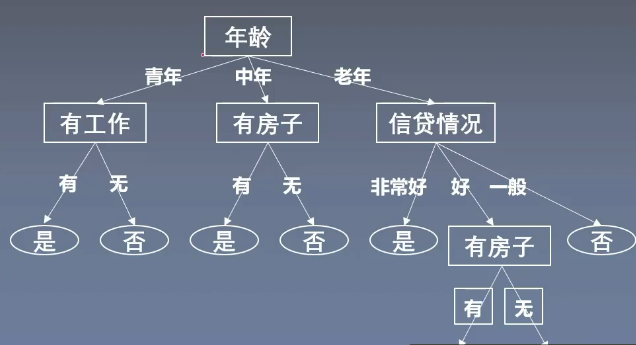
- 再举一个例子:我们有一个样本:老年,有工作,没房子,信贷情况好,那么我们就可以走这样的一条路
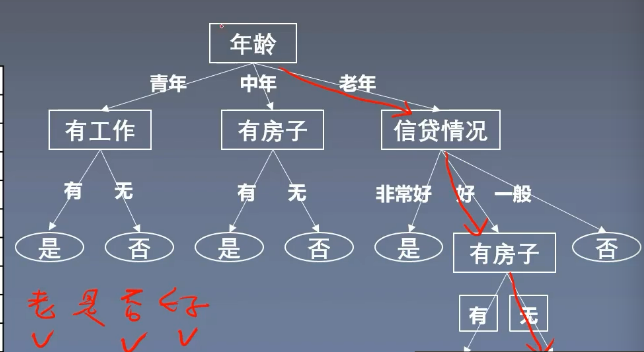
- 为什么先给年龄而不是先给工作呢?换句话说是怎么选择特征构建树的呢?
- 这不是我们人为决定的,而是要进行计算
1.2 熵
- 熵表示不确定性,定义如下:其中 nnn 为特征数,pip_ipi 表示一个概率
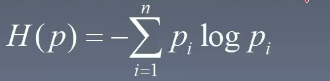
- 假设 n=2n=2n=2,则有:图中越靠近 p=0.5p=0.5p=0.5(即越不确定),熵就越大。这表明熵越大,随机变量的不确定性就越大
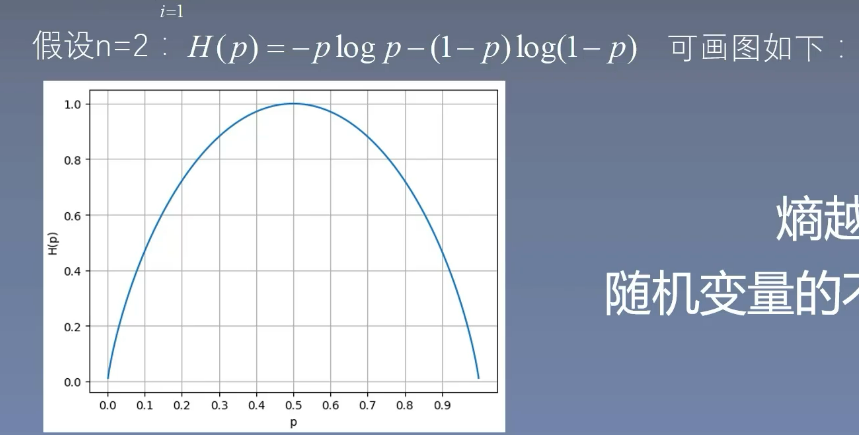
1.3 熵的计算举例
- 例:我们需要计算我们数据集的熵,计算数据集的熵要算的是目标变量(或叫做类别标签),在这里我们是计算是否给这个人贷款,即最后一列

- 我们把 DDD 称作我们的一个数据集,∣D∣|D|∣D∣ 表示数据集的条数,在这个例子为 ∣D∣=15|D|=15∣D∣=15
- kkk 表示目标变量的种类数,在这个例子为 k=2k=2k=2
- CkC_kCk 表示当前的这个类别条数有多个条,比如否有 6 条,那么 C1=6C_1=6C1=6
- 最后用下面的这个公式算出来即可
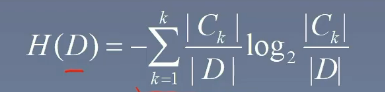
2. 条件熵
2.1 条件熵介绍
- 还是上节课的这个贷款数据集

- 条件熵的公式为含义为:在给定 X 为多少的条件下,计算 Y 的熵是多少
- 由于 X 有很多个取值,我们对它展开。比如之类年龄有青年,中年,老年
- 这里 pip_ipi 是变量 X 取值为 xix_ixi 的概率
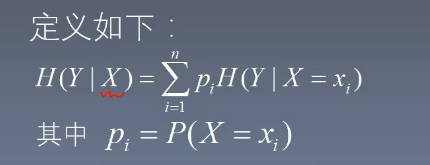
- 那么回到数据集的条件熵的计算公式来说,下面公式的含义如下:
- 这里的 AAA 为条件变量,比如年龄
- DDD 为数据集,∣D∣|D|∣D∣ 为数据集条数,∣Di∣|D_i|∣Di∣ 为条件变量当前取值的条数
- nnn 为条件的种类数
- KKK 依旧为目标变量的种类数
- ∣Dik∣|D_{ik}|∣Dik∣ 为两个变量同时满足的条数

2.2 条件熵的计算例子
- 我们以年龄为条件变量来尝试计算以它为条件的条件熵
- 以年龄为青年时为例子,我们 i=1i=1i=1 为青年,这里的 ∣D∣∣D1∣=515{|D| \over |D_1|}={5 \over {15}}∣D1∣∣D∣=155,总共有 555 个青年,然后右部的连加就是在以青年为条件下的目标变量的信息熵,所以有式子的右半部分的展开
- 对年龄的三个类别都做一次这样的操作后求连加即为以青年为条件的条件熵
3. 信息增益与 ID3 算法
3.1 信息增益
-
信息增益(也叫互信息)的定义如下:我们用符号 g(D,A)g(D,A)g(D,A) 来表示,即用数据集的信息熵减去以某个特征为条件的条件熵

-
根据信息增益准则的特征选择方法:
- 对训练数据集(或子集)D,计算其每个特征的信息增益
- 比较它们的大小,选择信息增益最大的特征
-
信息增益算法:
-
计算数据集 D 的信息熵 H(D):
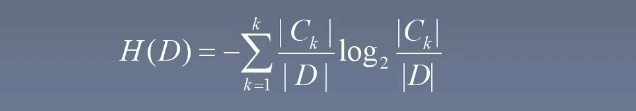
-
计算特征 A 对数据集 D 的经验条件熵 H(D|A)
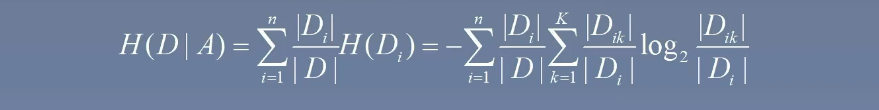
-
计算信息增益
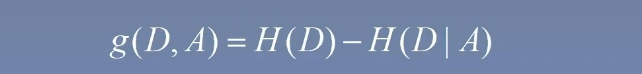
-
-
例子:
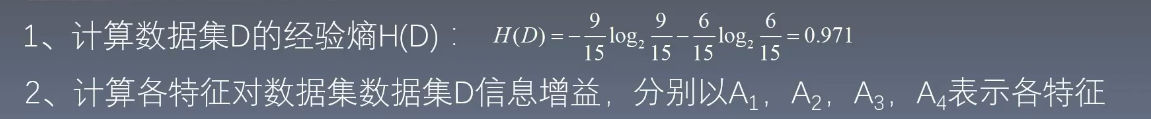

3.2 ID3 算法构建决策树
-
ID3 算法:在决策树递归构建过程中,使用信息增益的方法进行特征选择
-
决策树生成过程:
- 从根节点开始计算所有特征的信息增益,选择信息增益最大的特征作为结点特征
- 再对子节点递归调用以上方法,构建决策树
- 所有特征信息增益很小或没有特征可以选择时递归结束得到一颗决策树
-
比如说我们开始选择了 A3A_3A3 作为我们的根节点(根据上面的计算得到),此时我们会往下分叉出是或者否,然后我们又根据是或者否的子集来递归计算信息增益,比如是对应一个子集,否又对应一个子集