目录
- AOV和AOE
-
- [AOV 有向无环图及其应用(拓扑结构)](#AOV 有向无环图及其应用(拓扑结构))
- [AOE 有向无环图及其应用------关键路径](#AOE 有向无环图及其应用——关键路径)
-
- [1. 事件的最早发生时间](#1. 事件的最早发生时间)
- [2. 事件允许的最晚发生时间](#2. 事件允许的最晚发生时间)
- [3. 活动最早发生时间](#3. 活动最早发生时间)
- [4. 活动允许的最晚开始时间](#4. 活动允许的最晚开始时间)
AOV和AOE
AOV 有向无环图及其应用(拓扑结构)
AOV网------用顶点 表示活动 ,用弧 表示活动间优先关系 的有向图 称为顶点表示活动的网(Activity On Vertex network),简称AOV网
AOV网中不允许有回路,这意味着某项活动以自己为先决条件
拓扑排序 ------把AOV网络中各顶点 按照它们相互之间的优先关系 排列成一个线性序列的过程
检测AOV网中是否存在环 方法:对有向图 构造其顶点 的拓扑有序序列 ,若网中所有顶点 都在 它的拓扑有序序列 中,则该AOV网必定不存在环。
拓扑排序算法
- 选一个入度为0的顶点,输出;
- 删除该顶点以及由它出发的所有边
- 重复步骤1、2,直到全部顶点输出或不再存在入度为0的顶点;
- 若图中还有剩余顶点未被删除,说明图中有回路,不是一个AOV网
AOV网的拓扑序列不唯一
拓扑排序能够检测图中是否有环存在
图采用邻接表 存放;计算所有顶点的入度,存放于一维数组中;
cpp
// 结构体
#define MAXSIZE 100
typedef struct ArcNode{
int vex;
struct ArcNode* link;
} ArcNode; //弧
typedef struct VNode{
VertexType data;//顶点信息的数据类型
int id; //顶点的入度
ArcNode* firstarc;
}VNode; //顶点 顶点信息数组
typedef struct {
VNode arc[MAXSIZE];
int vexnum,arcnum;
//有向图
}Graphs;算法:
cpp
int topsort(Graphs T){
//图 T
int q[MAXSIZE], count, h=t=0;//队列指针初始化
//q为队列 用数组 顺序队列
ArcNode * p; // 弧
int u,v;
//1.计算所有顶点入度,将入度为0 的顶点放入队列; count=0;
for(v=0;v<T.vexnum;v++) //遍历所有顶点
T.arcs[v].id=0;//初始化
for (v=0;v<T.vexnum;v++)
for(p=T.arc[v].firstarc; p!=Null; p=p->link){
u=p->vex; //节点的信息存放的位置
T. arc[u].id++; //计算每个节点的入度
}
for (v=0;v<T.vexnum;v++)// 将入度为零的节点 入队
if (T. arc[v].id==0)
q[t++]=v;//自己加判断队列是否会溢出!
//开始拓扑排序
while (h!=t ){ //队列是否为空
v=q[h++]; //位置信息出队
printf("%d",v);//打印该位置信息的节点 v是位置信息 此处打印的是位置
count++; //计数
for(p=T.arc[v].firstarc; p!=Null;p=p->link){
//循环读取的是v节点 出度的所有节点
u=p->vex;
T. arc[u].id--;
if (T. arc[u].id==0)
q[t++]=u;//加判断队列是否会溢出!
}//每读取一个 就入队下一个
}
//
if (count<T.vexnum){//如果有节点没有被遍历到过 说明该图不是 联通图
printf("There is a cycle");
return 0;
}
else
return 1;
}
//总的时间复杂度为o(n+e)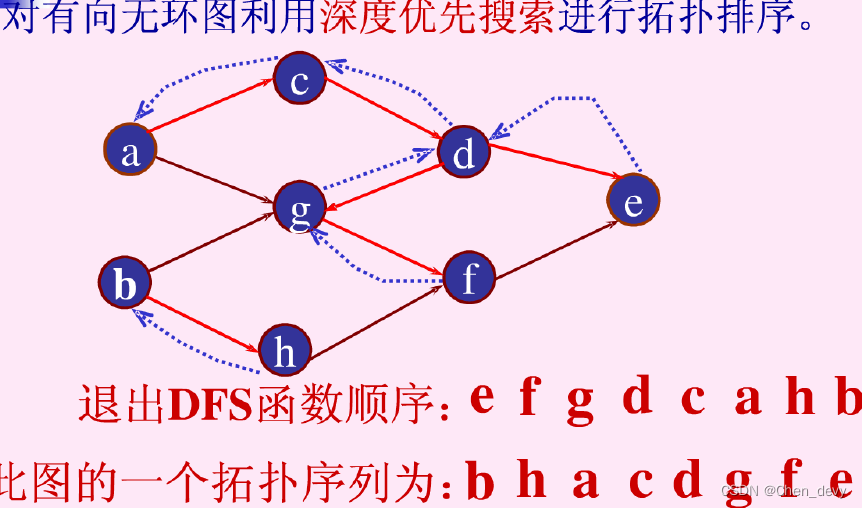
有向无环图的应用------存放表达式
中缀表达式 即运算符在操作数之间的表达式,常见表达式均为中缀表达式 。
后缀表达式 也叫逆波兰式
前缀表达式 也叫波兰式
二叉树存放表达式
二叉树存放表达式 :
波兰式:
+*dj/e+hi中缀表示:
d*j+e/(h+i)逆波兰式:
dj*ehi+/+
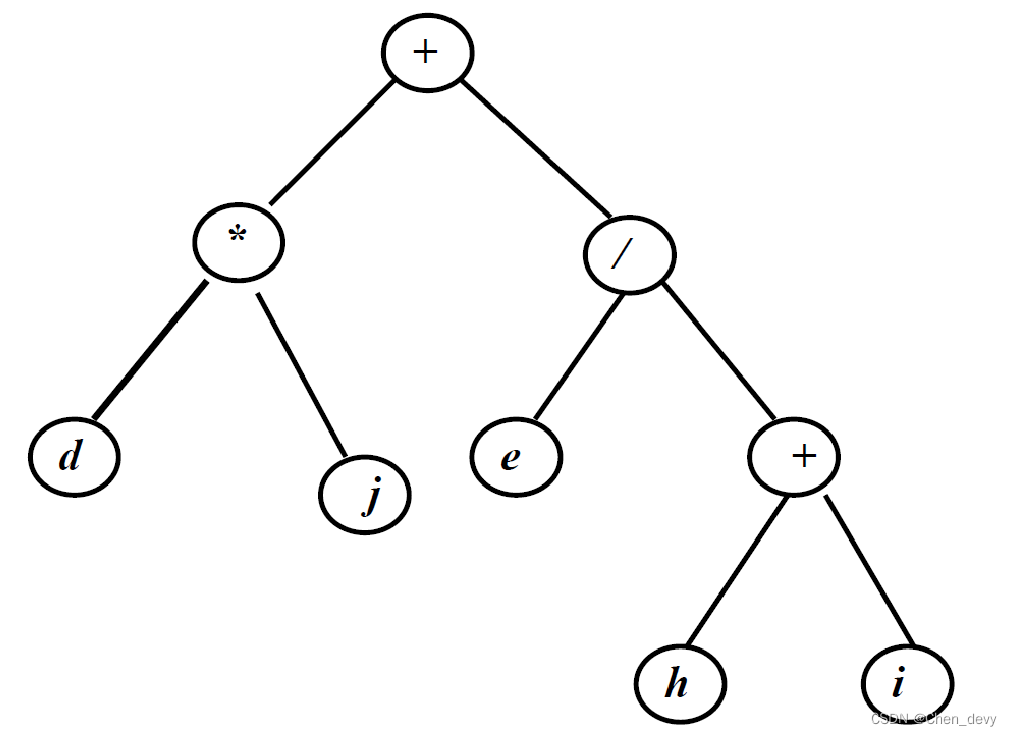
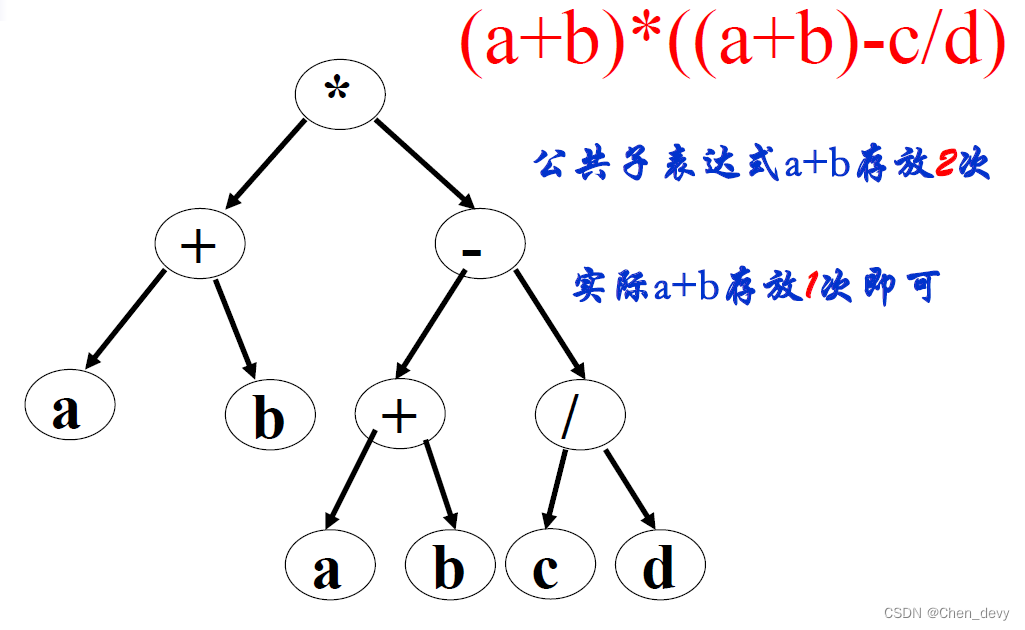
图存放表达式
图存放表达式可以优化公共子表达式,实现公共子表达式共享
特点:只有一个入度为0的顶点
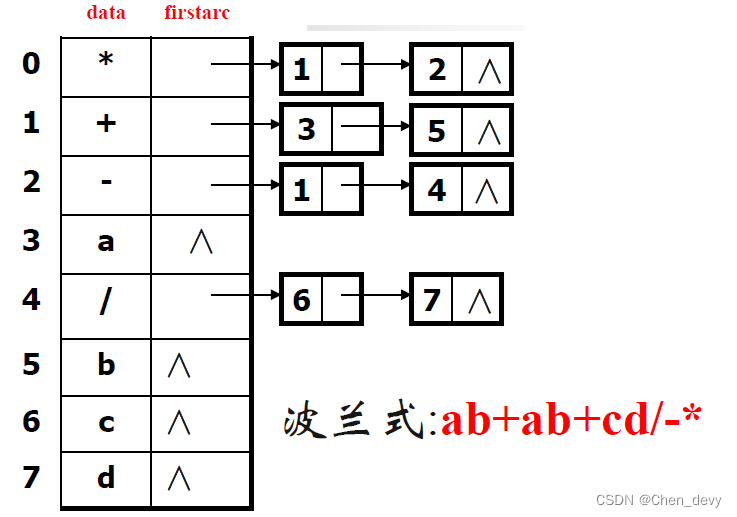
cpp
//构造逆波兰式的算法
Void s1(Graphs G){
int id[MAXSIZE];
for(v=0;v<G.vexnum;v++)
id[v]=0;
for (v=0;v<G.vexnum;v++)
for(p= G.arc[v].firstarc; p; p=p->link){
u=p->vex;
id[u]++;
}
for (v=0;v<G.vexnum;v++)
if(id[v]==0)
nibolan(G,v);
}
void nibolan(Graphs G,int v){
//从顶点v出发构造逆波兰式
if(G.arc[v].firstarc==NULL)
printf("%c",G.arc[v].data);
else {
p=G.arc[v].firstarc;
w=p->vex;
nibolan(G,w);
p=p->link;
w=p->vex;
nibolan(G,w);
printf("%c",G.arc[v].data);
}
}
//??AOE 有向无环图及其应用------关键路径
AOE网:表示工程计划的有向图 ,其中,顶点表示事件 ,弧表示活动 ,弧上的权值表示完成一项活动需要的时间
AOE网中的某些活动可以并行 进行,完成工程的最短时间 是从开始顶点到完成顶点的最长路径长度 。路径长度最长 的路径为关键路径 。关键路径 上所有活动 都叫做关键活动。
求解关键路径和关键活动通过事件的最早、最迟发生时间、活动的最早、最迟发生时间完成。
只有在某顶点 代表的事件 发生后,从该顶点 发出去的弧 所代表的各项活动 才能开始
只有进入 某顶点的各条弧代表的活动 都已经结束,该顶点所代表的事件才能发生 (*)
1. 事件的最早发生时间
使用一维数组ve[]来保存每一事件的最早发生时间。
事件 v i v_i vi的最早发生时间ve[i]是从开始顶点 v 1 v_1 v1到顶点 v i v_i vi的最长路径长度 。
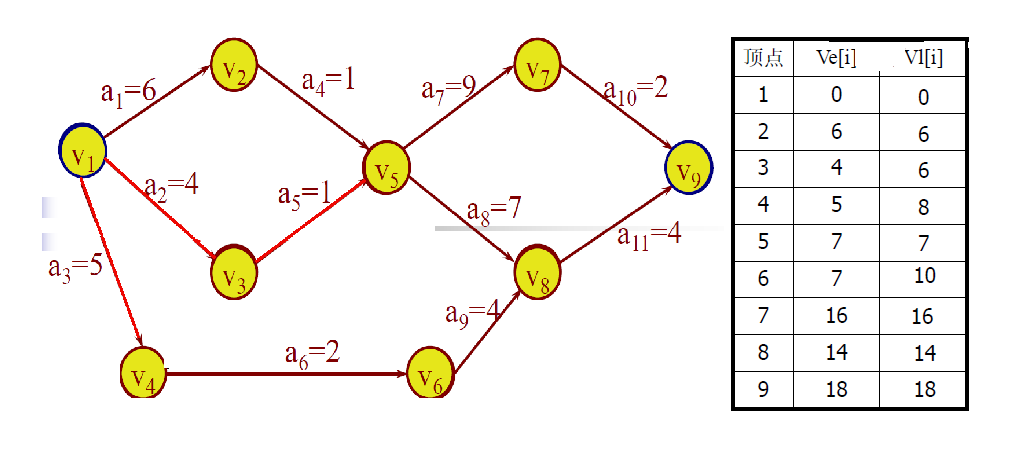
事件(顶点)最早发生时间的计算方法:
从开始顶点 v 1 v_1 v1出发,令ve[1]=0,按拓扑有序 求其余各顶点 的最早发生时间ve[k](2≤k≤n)
ve[k] = max{ve[j]+dut(<j,k>): <j,k>∈S},dut(<j,k>)表示活动<j,k>的所需的时间,其中S是以顶点v_k为弧头的所有弧的集合。
2. 事件允许的最晚发生时间
一维数组vl []保存每一事件允许的最晚发生时间
事件 v i v_i vi允许的最晚发生时间 vl[i]是在保证完成顶点 v n v_n vn在ve[n]时刻发生的前提下,事件 v i v_i vi允许发生的最晚时间 ,它等于ve[n]减去 v i v_i vi到 v n v_n vn的最长路径长 度。
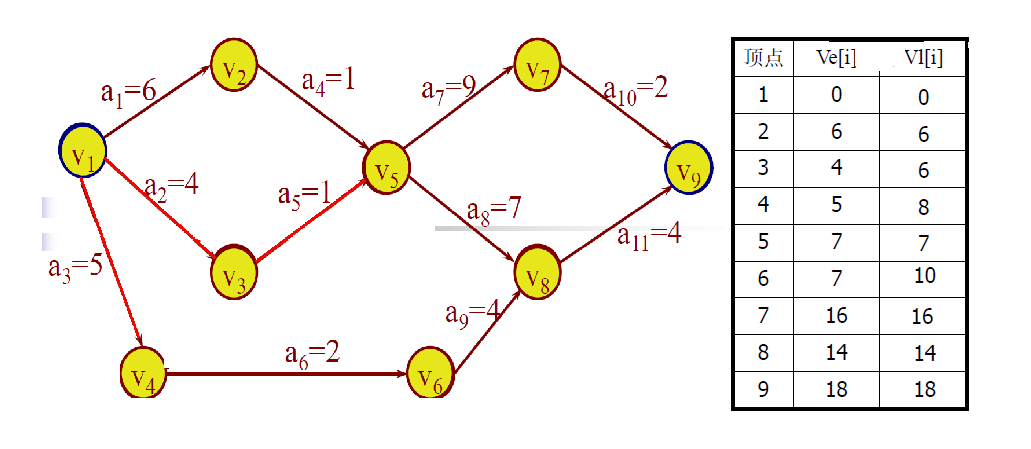
事件(顶点)允许的最晚发生时间的计算方法:
从完成顶点 v n v_n vn出发,令vl[n]=ve[n],按逆拓扑有序求其余各顶点的允许的最晚发生时间vl[i] (n-1≥i≥1)
vl[i]=min{vl[k]-dut(<i,k>): <i,k>∈S}其中S是以顶点vi为弧尾的所有弧的集合。
3. 活动最早发生时间
■ 一维数组e []保存每一活动的最早发生时间
■ 设活动 a i a_i ai用弧 < v j , v k > <v_j,v_k> <vj,vk>表示,与 a i a_i ai相联系的权值 dut(<j,k>)用表示,则 a i a_i ai的可能的最早开始时间e[i]等于事件 v j v_j vj可能的最早发生时间ve[j]。
4. 活动允许的最晚开始时间
设活动 a i a_i ai用弧 < v j , v k > <v_j,v_k> <vj,vk>表示,与 a i a_i ai相联系的权值dut(<j,k>)用表示,则活动 a i a_i ai允许的最晚开始时间l[i]等于事件 v k v_k vk允许的最晚发生时间vl[k]-dut(<j,k>)。
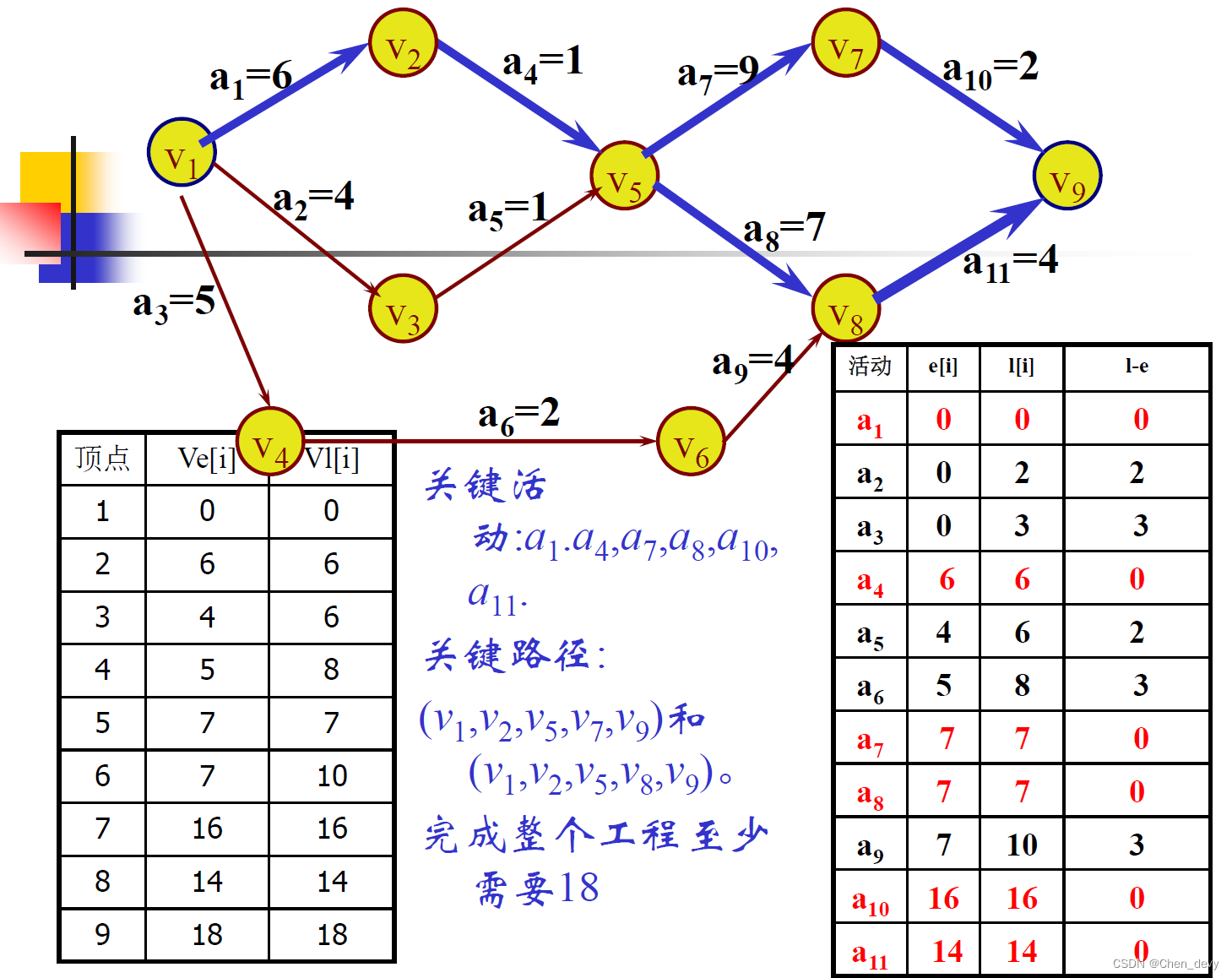
(1)关键路径上 所有的活动都是关键活动 。因此提前完成非关键活动并不能加快工程的速度。
(2)网络中的关键路径并不唯一,对于有几条关键路径的网来说,仅仅提高某一条关键路径上关键活动的速度,是不能缩短整个工程工期的,而必须同时提高几条关键路径上关键活动的速度。
所以,并不是网中任何一个关键活动的提前完成,整个工程都能提前完成。