TIE:时间间隔误差(Time Interval Error,简称TIE)抖动,即在很长的一串波形中,每次边缘的位置相对理想clk 的抖动。
TJ@BER :TJ(Total Jitter)总体抖动,为某误码率(Bit Error Ratio,简称BER)下抖动的峰峰值。 其中 @BER 表示 误码率为 10e-12 下的的Tj。即 假设 大约每10e12次传送会有一次抖动大于 t,t 即定义为此时的 TJ值。
TJ 的构成:由 "随机抖动"(RJ, Random Jitter)和"确定性抖动"(DJ - Deterministic Jitter)组成 。确定性抖动进一步可分为周期抖动(PJ,period jitter)和数据相关抖动(DDJ,data dependent jitter),数据相关抖动可进一步分为占 空比失真(DCD)和符码间干扰(ISI)。
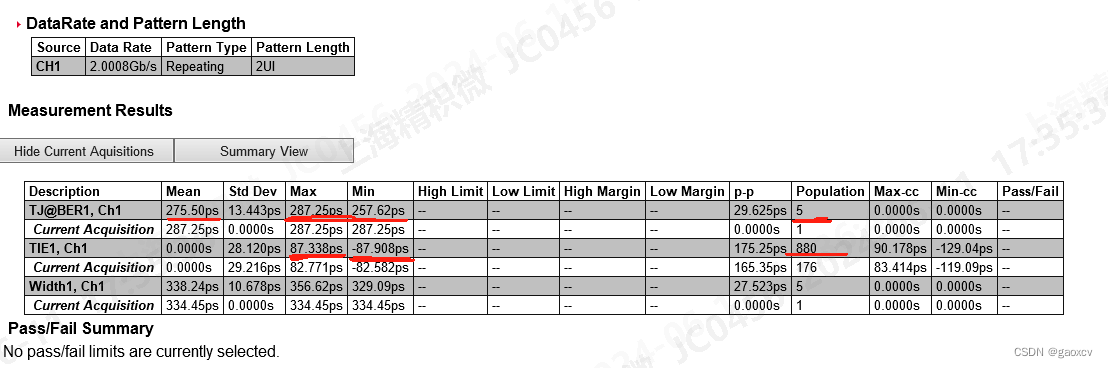
**TIE 和 TJ 的关系:**如下图测量结果
TIE 是 以一共 880次(分5次,每次166采样)采样,实际边缘与理想边缘差值的 880个结果进行统计,得到最大值87ps,最小值-87ps,均方差28ps
880次结果会有一个统计直方图(其实就是概率密度函数PDF probability density)如左下图蓝色的部分,通过拟合插入绿色的部分,将此图扩展为右图,然后查找y值 即可得到能保证 10e-12 误码率(BER,bit error rate)(即抖动大于此x值的概率小于 1/10e12) 对应的 x值,即为TJ@BER。
5次测试,每次只给一个TJ@BER,统计可得5次TJ 的min(257ps),和max(287ps)

从TIE 到 TJ@BER 的换算还涉及到 累计分布函数(CDF,Cumulative Distribution Function),取对数等操作,具体过程可参考下面的链接。
https://www.zhihu.com/question/35065974/answer/3362657464