【力扣】矩阵中的最长递增路径

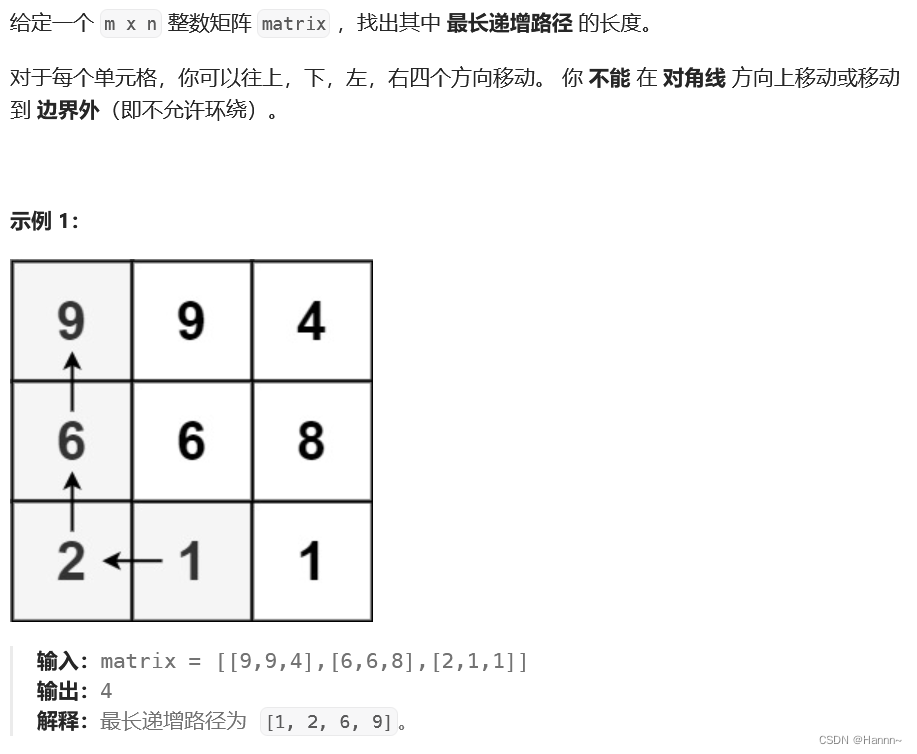
一、题目描述

二、解题思路

1、先求出以矩阵中的每个单元格为起点的最长递增路径

题目中说，对于每个单元格，你可以往上，下，左，右四个方向移动 。那么以一个单元格为起点的最长递增路径就是：从该单元格往上，下，左，右四个方向走的四条递增路径中的最大值（即最长的一条递增路径）。

2、在求出的所有最长递增路径中找最大值

因为题目是求矩阵中的最长递增路径 ，所以要在求出的所有最长递增路径中找最大值。

3、使用"记忆化搜索"（递归+"备忘录" ）来解决该题。

三、 代码

class Solution {
    int m, n;

    //遍历上、下、左、右四个方向所需的数组
    int[] dx = {0,0,1,-1};
    int[] dy = {1,-1,0,0};

    int[][] memo;  //备忘录
    public int longestIncreasingPath(int[][] matrix) {
        m = matrix.length;
        n = matrix[0].length;
        memo = new int[m][n];

        //求所有的最长递增路径中的最大值
        int ret = 0;
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                ret = Math.max(ret,dfs(i, j, matrix));
            }
        }
        return ret;
    }

    //递归函数
    //求出以矩阵中的每个单元格为起点的最长递增路径（上下左右四个方向中的最大值）
    public int dfs(int i, int j, int[][] matrix) {
        if(memo[i][j] != 0) {
            return memo[i][j];
        }
        int ret = 1;
        for(int k = 0; k < 4; k++) {
            int x = i + dx[k];
            int y = j + dy[k];
            if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j]) {
                ret = Math.max(ret, dfs(x,y,matrix)+1);
            }
        }
        memo[i][j] = ret;
        return ret;
    }
}