5. 最长回文子串

自己做
思路1:暴力解,超时

cpp
class Solution {
public:
bool checkPalindrome(const string s) {
int len = s.size(); //长度
int mid = len / 2; //中轴
if (len % 2 == 1) { //子串长为奇数的情况
for (int i = 0; i <= mid; i++) {
if (s[mid - i] != s[mid + i]) //发现不对称,即表示这个子串不是回文串
return false;
}
}
else { //子串长为偶数的情况
for (int i = 0; i < mid; i++) {
if (s[i] != s[len - 1 - i]) //发现不对称,即表示这个子串不是回文串
return false;
}
}
return true;
}
string longestPalindrome(string s) {
int len = s.size(); //字符串长度
int max = 1; //最大长【默认一个字符为回文串】
string c; //保存目前子串
int begin = 0, end = 0; //最长子串的起始和结束位置
for (int i = 0; i < len; i++) { //子串起始
c = s[i]; //重置子串
for (int j = i + 1; j < len; j++) { //子串延伸
c += s[j]; //延伸子串
if (c.size() <= max) { //必然不可能是最长子串,跳过检测
}
else if (checkPalindrome(c) && c.size() > max) { //更新最长子串【目前的i和j】
begin = i;
end = j;
max = j - i + 1; //更新最长长度
}
}
}
//目前已经找到了最长回文串
c = ""; //重置子串
for (int i = begin; i <= end; i++) {
c += s[i];
}
return c;
}
};思路2:
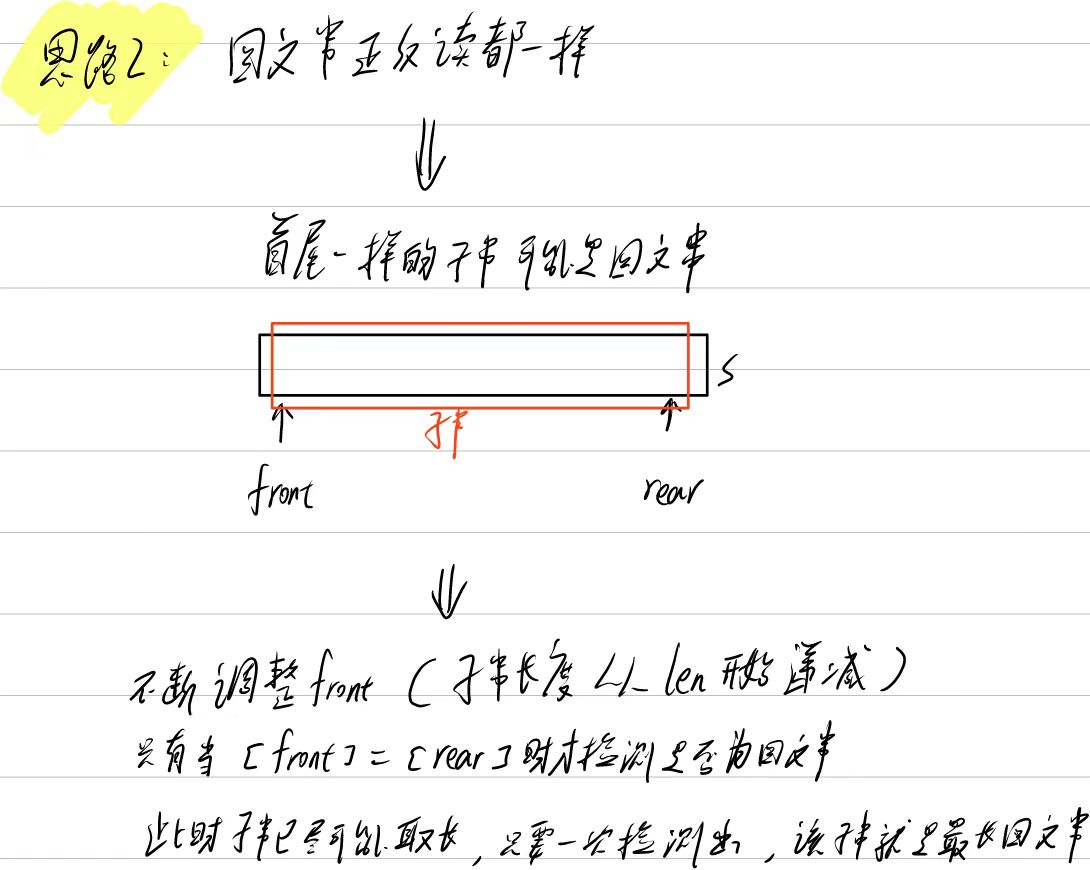
cpp
class Solution {
public:
bool checkPalindrome(const string s,int front,int len) {
int mid = len / 2; //中轴
if (len % 2 == 1) { //子串长为奇数的情况
for (int i = 0; i <= mid; i++) {
if (s[front + mid - i] != s[front + mid + i]) //发现不对称,即表示这个子串不是回文串
return false;
}
}
else { //子串长为偶数的情况
for (int i = 0; i < mid; i++) {
if (s[front + i] != s[front + len - 1 - i]) //发现不对称,即表示这个子串不是回文串
return false;
}
}
return true;
}
string longestPalindrome(string s) {
int len = s.size(); //字符串长度
string c = ""; //保存目前子串
for (int c_len = len; c_len > 0; c_len--) { //子串长度从len开始递减
for (int front = 0; front + c_len <= len; front++) { //子串
if (s[front] == s[front + c_len - 1]) { //只有当首尾字符一致才检测是否回文串
if (checkPalindrome(s,front, c_len)) { //检测是否回文串
//目前已经找到了最长回文串
for (int i = front; i <= front + c_len - 1; i++) {
c += s[i];
}
return c;
}
}
}
}
//找不到的情况
c += s[0];
return c;
}
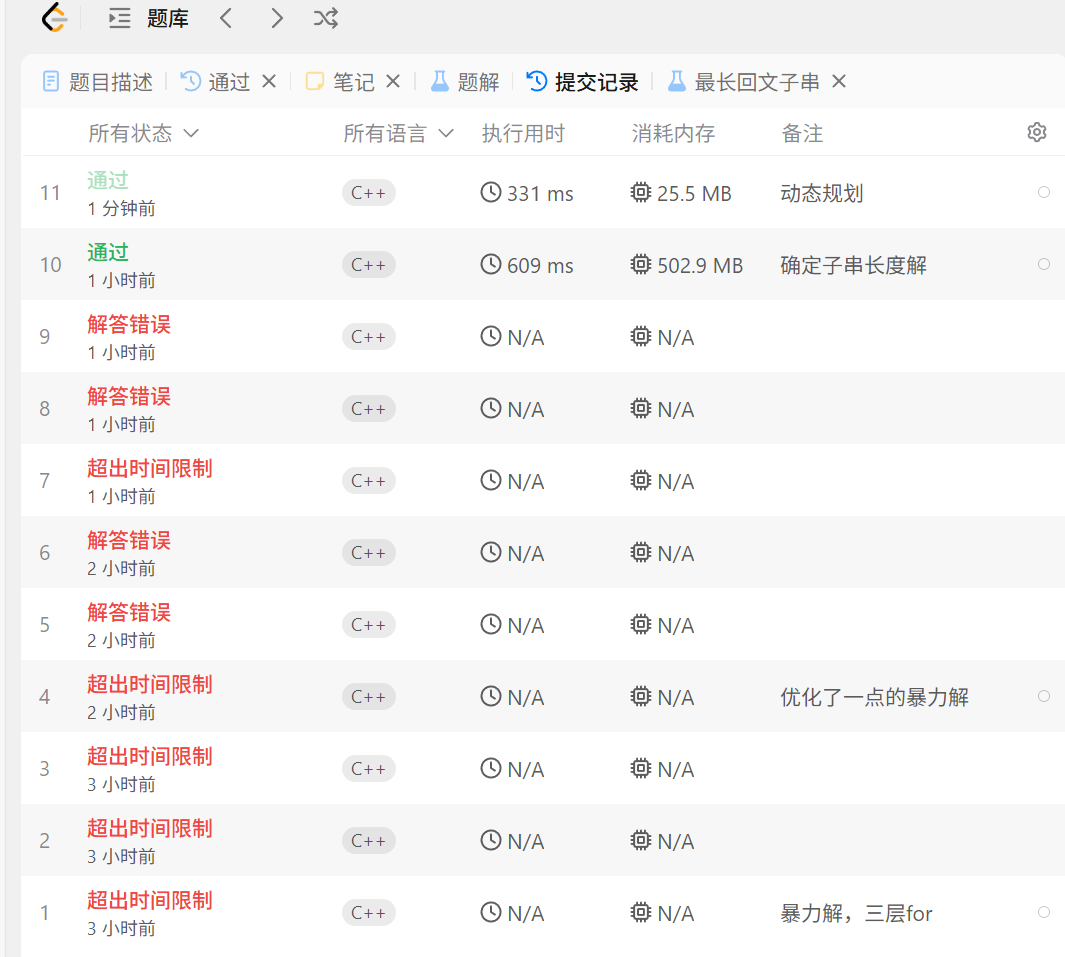
};看题解【想不出最优解】


cpp
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
if (n < 2) { //只有一个字符的边界情况
return s;
}
int max = 1; //最大回文串长
int begin = 0; //最长回文串起始
vector<vector<bool>> dp(n, vector<bool>(n)); //初始化dp[n][n]标记数组
for (int i = 0; i < n; i++)
dp[i][i] = true; //所有的单个字符都是回文串
for (int len = 2; len <= n; len++) { //子串长度
for (int i = 0; i < n; i++) { //子串起始位置
int j = i + len - 1; //子串末尾
if (j >= n) //超出边界
break;
if (s[i] != s[j]) { //左右两边不相等
dp[i][j] = false; //必然不是回文串
}
else { //左右两边相等
if (j - i < 3) { //偶数或者三个字符的情况
dp[i][j] = true;
}
else {
dp[i][j] = dp[i + 1][j - 1]; //本来是回文串现在还是回文串,本来不是回文串就不可能是回文串
}
}
if (dp[i][j] && j - i + 1 > max) { //如果该段是回文串且长度超过了之前的最大长,更新
max = len;
begin = i;
}
}
}
//此时得到了最大回文串的长度和起始位置
return s.substr(begin, max);
}
};
今日总结
回去重新把算法书捡起来