文章目录
- [SVM 分类器的误差函数](#SVM 分类器的误差函数)
- [非线性边界的 SVM 分类器(内核方法)](#非线性边界的 SVM 分类器(内核方法))
源代码文件请点击此处!
SVM 分类器的误差函数
SVM 使用两条平行线,使用中心线作为参考系 L : w 1 x 1 + w 2 x 2 + b = 0 L: \ w_1x_1 + w_2x_2 + b = 0 L: w1x1+w2x2+b=0。我们构造两条线,一条在上面,一条在下面,分别为:
L + : w 1 x 1 + w 2 x 2 + b = 1 L − : w 1 x 1 + w 2 x 2 + b = − 1 L+: \ w_1x_1 + w_2x_2 + b = 1 \\ L-: \ w_1x_1 + w_2x_2 + b = -1 L+: w1x1+w2x2+b=1L−: w1x1+w2x2+b=−1
分类器由 L + L+ L+ 和 L − L- L− 组成。为训练 SVM,我们需要为由两条线组成的分类器构建一个误差函数,期望达成的目标有两个:
- 两条线中的每一条都应尽可能对点进行分类。
- 两条线应尽可能彼此远离。
误差函数表示如下:
误差 = 分类误差 + 距离误差 误差 = 分类误差 + 距离误差 误差=分类误差+距离误差
分类误差函数
点 ( x 1 , x 2 ) (x_1, x_2) (x1,x2) 的预测函数为
y ^ = s t e p ( w 1 x 1 + w 2 x 2 + b ) \hat{y} = step(w_1x_1 + w_2x_2 + b) y^=step(w1x1+w2x2+b)
显然这是一个离散感知器,其中:
y = s t e p ( x ) = { 0 , x ≤ 0 1 , x > 0 y = step(x) = \begin{cases} 0, x \leq 0 \\ 1, x > 0 \end{cases} y=step(x)={0,x≤01,x>0
定义分类误差函数如下:
{ 0 , 错误分类 ∣ w 1 x 1 + w 2 x 2 + b ∣ , 正确分类 \begin{cases} 0, 错误分类 \\ |w_1x_1 + w_2x_2 + b|, 正确分类 \end{cases} {0,错误分类∣w1x1+w2x2+b∣,正确分类
例如,考虑标签为 0 0 0 的点 ( 4 , 3 ) (4,3) (4,3),两个感知器给出的预测为:
L + : y ^ = s t e p ( 2 x 1 + 3 x 2 − 7 ) = 1 L − : y ^ = s t e p ( 2 x 1 + 3 x 2 − 5 ) = 1 L+: \hat{y} = step(2x_1 + 3x_2 - 7) = 1 \\ L-: \hat{y} = step(2x_1 + 3x_2 - 5) = 1 L+:y^=step(2x1+3x2−7)=1L−:y^=step(2x1+3x2−5)=1
可以看到两个感知器均预测错误,此时分类误差为:
∣ 2 x 1 + 3 x 2 − 7 ∣ + ∣ 2 x 1 + 3 x 2 − 5 ∣ = 22 |2x_1 + 3x_2 - 7| + |2x_1 + 3x_2 - 5| = 22 ∣2x1+3x2−7∣+∣2x1+3x2−5∣=22
距离误差函数
若两个线性方程如下:
L + : w 1 x 1 + w 2 x 2 + b = 1 L − : w 1 x 1 + w 2 x 2 + b = − 1 L+: \ w_1x_1 + w_2x_2 + b = 1 \\ L-: \ w_1x_1 + w_2x_2 + b = -1 L+: w1x1+w2x2+b=1L−: w1x1+w2x2+b=−1
根据两条平行直线间的距离公式:
d = ∣ C 1 − C 2 ∣ A 2 + B 2 d = \frac{|C_1 - C_2|}{\sqrt{A^2 + B^2}} d=A2+B2 ∣C1−C2∣
则这两条平行线的垂直距离为:
d = 2 w 1 2 + w 2 2 d = \frac{2}{\sqrt{w_1^2 + w_2^2}} d=w12+w22 2
此为距离误差。注意到,当 w 1 2 + w 2 2 w_1^2 + w_2^2 w12+w22 很大时, d d d 很小;当 w 1 2 + w 2 2 w_1^2 + w_2^2 w12+w22 很小时, d d d 很大。因此 w 1 2 + w 2 2 w_1^2 + w_2^2 w12+w22 是一个很好的误差函数。
C 参数
很多时候我们希望 SVM 分类器能侧重于分类误差或距离误差其中一个方面,那么我们可以使用 C 参数:
误差 = C ⋅ 分类误差 + 距离误差 误差 = C \cdot 分类误差 + 距离误差 误差=C⋅分类误差+距离误差
C 参数如何控制两者的呢?
- C 很大:误差公式以分类误差为主,SVM 分类器更侧重于对点进行正确分类;
- C 很小:误差公式以距离误差为主,SVM 分类器更侧重于保持线之间的距离。
下面是一个例子:
python
svm_c_001 = SVC(kernel='linear', C=0.01)
svm_c_001.fit(features, labels)
svm_c_100 = SVC(kernel='linear', C=100)
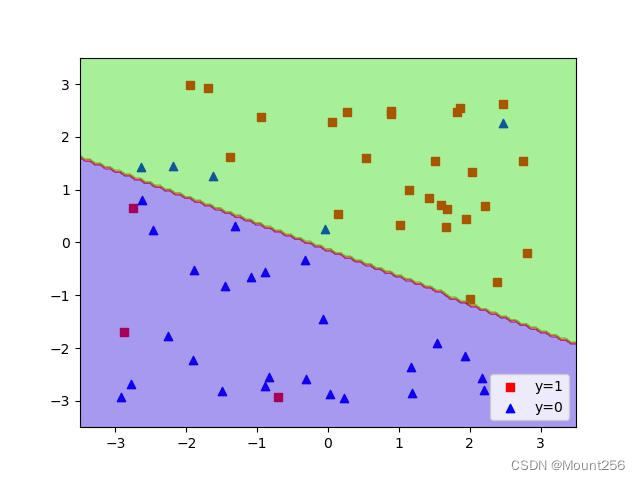
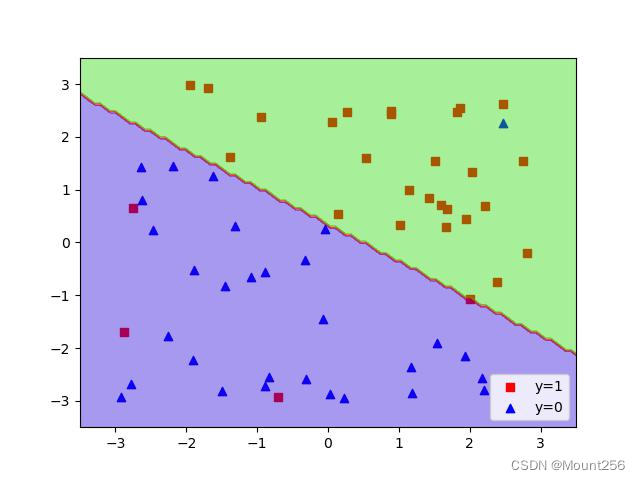
svm_c_100.fit(features, labels)上图为 C=0.01 的情况,下图为 C=100 的情况:
非线性边界的 SVM 分类器(内核方法)
多项式内核
- 在变量 x 1 , x 2 x_1, x_2 x1,x2 使用 2 阶多项式内核,就需要计算这些单项式: x 1 , x 2 , x 1 2 , x 1 x 2 , x 2 2 x_1, x_2, x_1^2, x_1x_2, x_2^2 x1,x2,x12,x1x2,x22,然后尝试把它们线性组合起来,比如通过检查发现这是一个有效的分类器公式: x 1 2 + x 2 2 = 1 x_1^2 + x_2^2 = 1 x12+x22=1
- 这相当于将二维平面映射到一个五维平面,即点 ( x 1 , x 2 ) (x_1, x_2) (x1,x2) 到点 ( x 1 , x 2 , x 1 2 , x 1 x 2 , x 2 2 ) (x_1, x_2, x_1^2, x_1x_2, x_2^2) (x1,x2,x12,x1x2,x22) 的映射
- 类似地,在变量 x 1 , x 2 x_1, x_2 x1,x2 使用 3 阶多项式内核,就需要计算这些单项式: x 1 , x 2 , x 1 2 , x 1 x 2 , x 2 2 , x 1 3 , x 1 2 x 2 , x 1 x 2 2 , x 2 3 x_1, x_2, x_1^2, x_1x_2, x_2^2, x_1^3, x_1^2x_2, x_1x_2^2, x_2^3 x1,x2,x12,x1x2,x22,x13,x12x2,x1x22,x23,然后尝试把它们线性组合起来,通过检查发现一个有效的分类器公式
代码如下:
python
svm_degree_2 = SVC(kernel='poly', degree=2)
svm_degree_2.fit(features, labels)
print("[Degree=2] Accuracy=", svm_degree_2.score(features, labels))
svm_degree_4 = SVC(kernel='poly', degree=4)
svm_degree_4.fit(features, labels)
print("[Degree=4] Accuracy=", svm_degree_4.score(features, labels))当分类器为 2 阶多项式的运行结果:
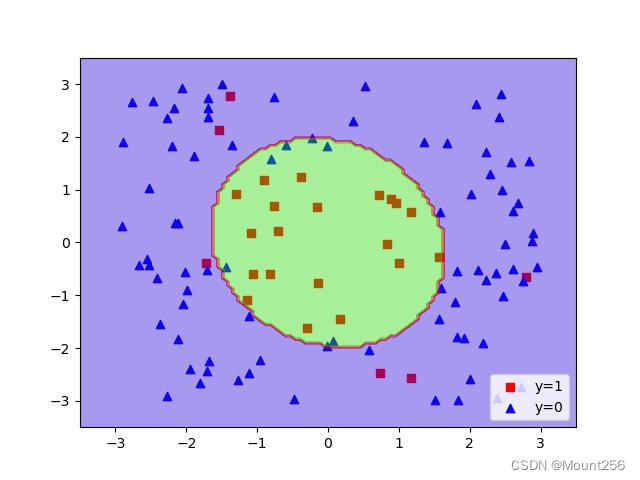
当分类器为 4 阶多项式的运行结果:
径向基函数(RBF)内核
径向基函数:
- 当变量只有一个时,最简单的径向基函数为 y = e − x 2 y = e^{-x^2} y=e−x2,此函数看起来像标准正态分布,函数凸起处为 x = 0 x=0 x=0
- 当变量有 2 个时,最简单的径向基函数为 z = e − ( x 2 + y 2 ) z = e^{-(x^2 + y^2)} z=e−(x2+y2),此函数看起来像标准正态分布,函数凸起处为 ( 0 , 0 ) (0,0) (0,0)
- 当变量有 n n n 个时,基本径向基函数为 y = e − ( x 1 2 + . . . + x n 2 ) y = e^{-(x_1^2 + ... + x_n^2)} y=e−(x12+...+xn2), n n n 维凸点以 0 为中心
- 若希望以点 ( p 1 , . . . , p n ) (p_1, ..., p_n) (p1,...,pn) 为中心凸起,则基本径向基函数为 y = e − [ ( x 1 − p 1 ) 2 + . . . + ( x n − p n ) 2 ] y = e^{-[(x_1-p_1)^2 + ... + (x_n-p_n)^2]} y=e−[(x1−p1)2+...+(xn−pn)2]
- 添加 γ \gamma γ 参数: y = e − γ [ ( x 1 − p 1 ) 2 + . . . + ( x n − p n ) 2 ] y = e^{-\gamma[(x_1-p_1)^2 + ... + (x_n-p_n)^2]} y=e−γ[(x1−p1)2+...+(xn−pn)2],用于控制拟合程度(形象理解,即调整凸起程度 )
- 当 γ \gamma γ 值非常小时,模型会欠拟合
- 当 γ \gamma γ 值非常大时,模型会严重过拟合,合适的 γ \gamma γ 值非常重要
相似度公式:
- 对于点 p p p 和点 q q q, 相似度 ( p , q ) = e − 距离 ( p , q ) 2 相似度(p,q) = e^{-距离(p,q)^2} 相似度(p,q)=e−距离(p,q)2
- 一维数据集中,点 x 1 x_1 x1 和点 x 2 x_2 x2 的相似度为 e − ( x 1 − x 2 ) 2 e^{-(x_1-x_2)^2} e−(x1−x2)2
- 二维数据集中,点 A ( x 1 , y 1 ) A(x_1, y_1) A(x1,y1) 和点 B ( x 2 , y 2 ) B(x_2, y_2) B(x2,y2) 的相似度为 e − [ ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 ] e^{-[(x_1-x_2)^2 + (y_1-y_2)^2]} e−[(x1−x2)2+(y1−y2)2]
- 若该数据集有 n n n 个数据点,则应计算 n 2 n^2 n2 个相似度;每个点到自身的相似度一定为 1;距离越近,相似度越高
有了相似度公式,就可以定义分类器了。假设数据集有 n n n 个数据点 X i X_i Xi,每个点对应标签 L i L_i Li(取值为 0 或 1),则对于点 X X X 的分类预测如下:
y ^ = s t e p [ ∑ i = 1 n ( − 1 ) L i − 1 ⋅ e − 距离 ( X , X i ) 2 ] \hat{y} = step[\sum^n_{i=1} (-1)^{L_i - 1} \cdot e^{-距离(X, X_i)^2}] y^=step[i=1∑n(−1)Li−1⋅e−距离(X,Xi)2]
形象理解:这相当于在一个二维平面上,为标记为 0 的点添加了一个"山谷",为标记为 1 的点添加了一个"山峰"。对每个点都如此操作,最后使用阈值 0 画出一个"海岸线",这就是最后的分类边界(boundary)。
代码如下:
python
svm_gamma_01 = SVC(kernel='rbf', gamma=0.1)
svm_gamma_01.fit(features, labels)
print("[Gamma=0.1] Accuracy=", svm_gamma_01.score(features, labels))
svm_gamma_1 = SVC(kernel='rbf', gamma=1)
svm_gamma_1.fit(features, labels)
print("[Gamma=1] Accuracy=", svm_gamma_1.score(features, labels))
svm_gamma_10 = SVC(kernel='rbf', gamma=10)
svm_gamma_10.fit(features, labels)
print("[Gamma=10] Accuracy=", svm_gamma_10.score(features, labels))
svm_gamma_100 = SVC(kernel='rbf', gamma=100)
svm_gamma_100.fit(features, labels)
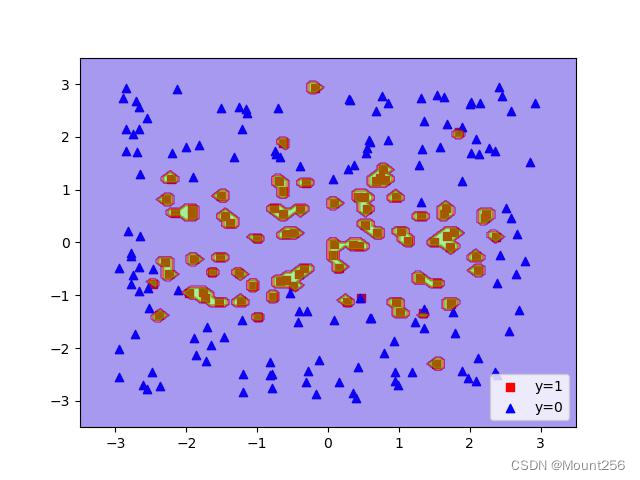
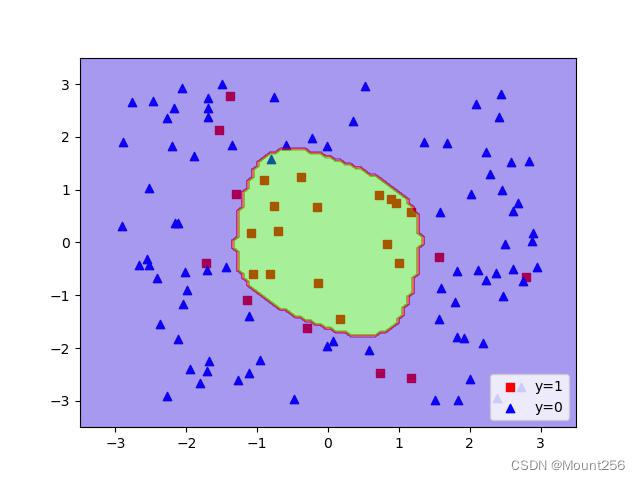
print("[Gamma=100] Accuracy=", svm_gamma_100.score(features, labels))γ = 0.1 \gamma=0.1 γ=0.1 时的运行结果:
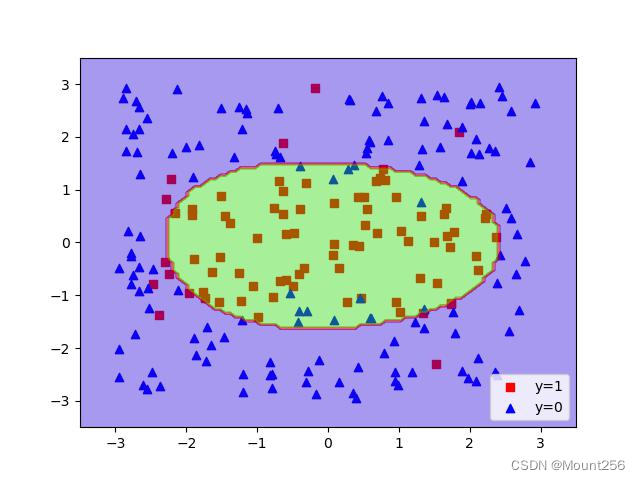
γ = 1 \gamma=1 γ=1 时的运行结果:
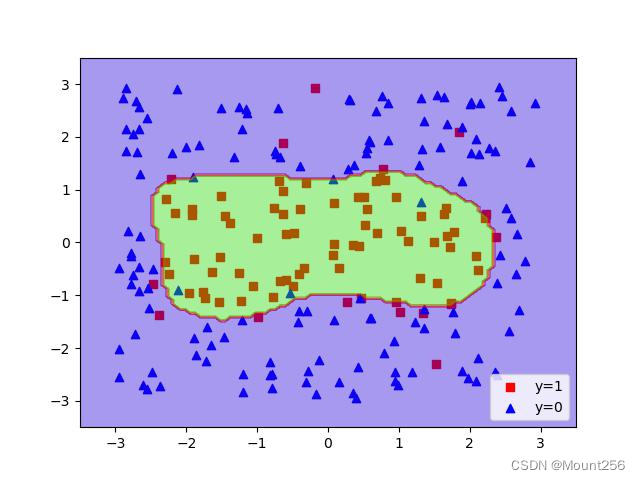
γ = 10 \gamma=10 γ=10 时的运行结果:
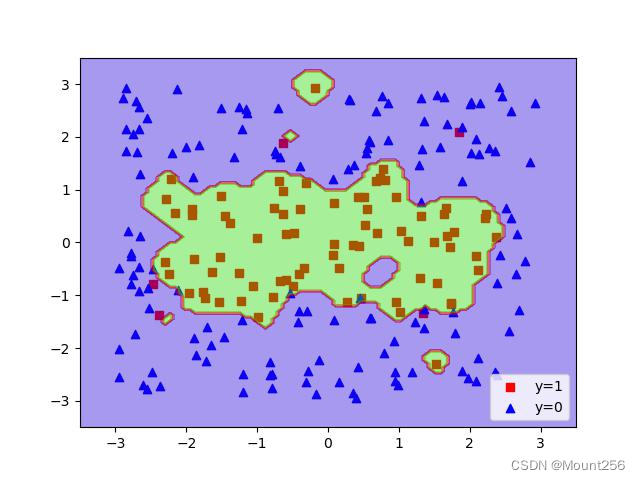
γ = 100 \gamma=100 γ=100 时的运行结果: