极限存在的条件
在左极限与又极限相关的内容中我们知道极限(也叫双侧极限)存在的充分必要条件是左右极限都存在且相等,否则极限不存在。所以这里要来详细的探讨一下在什么情况下函数会不存在极限。
1. 函数 f ( x ) = 1 x f(x)=\frac{1}{x} f(x)=x1
观察反比例函数 f ( x ) = 1 / x f(x) = 1/x f(x)=1/x 的图像,如图所示. lim x → 0 f ( x ) \lim_{x \rightarrow 0}f(x) limx→0f(x) 是什么呢?看图就知道双侧极限在这里不大可能存在。因此,我们先来试着求一下右极限, l i m x → 0 + f ( x ) lim_{x \rightarrow 0+}f(x) limx→0+f(x)。

看一下图像,当 x x x 是正的且接近于 0 0 0 时, f ( x ) f(x) f(x) 看起来好像非常大,特别是当 x x x 从右侧滑向 0 0 0 时,它看起来并不接近于任何数,它就是变得越来越大了。但会有多大呢?它会比你能想象到的任何数都大!我们说该极限是无穷大,并写作:
lim x → 0 + 1 x = ∞ \lim_{x \rightarrow 0+} \frac{1}{x}=\infty x→0+limx1=∞
类似地,这里的左极限是 − ∞ −\infty −∞,因为当 x x x 向 0 0 0 上升时, f ( x ) f(x) f(x) 会变得越来越负,这就是说
lim x → 0 − 1 x = − ∞ \lim_{x \rightarrow 0-} \frac{1}{x}=-\infty x→0−limx1=−∞
由于左极限为 − ∞ -\infty −∞ 和右极限为 + ∞ +\infty +∞ 不相等,故左极限和右极限都存在,但是双侧极限显然不存在。
2. 函数 g ( x ) = 1 x 2 g(x)=\frac{1}{x^2} g(x)=x21
观察反比例函数 g ( x ) = 1 x 2 g(x)=\frac{1}{x^2} g(x)=x21 的图像,如图所示 lim x → 0 f ( x ) \lim_{x \rightarrow 0}f(x) limx→0f(x) 是什么呢?
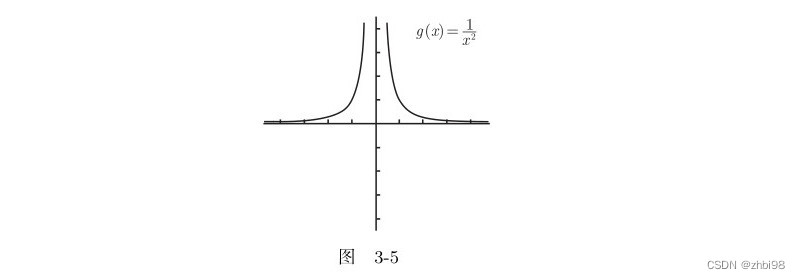
此函数在 x = 0 x=0 x=0 处的左极限和右极限都是 ∞ \infty ∞,因为左极限等于右极限,故左极限和右极限以及双侧极限都存在,因此这时也可以说极限(合称为极限)存在,即符号表示为 lim x → 0 1 x 2 = ∞ \lim_{x \rightarrow 0}\frac{1}{x2}=\infty limx→0x21=∞。
3. 函数 g ( x ) = s i n ( 1 x ) g(x)=sin(\frac{1}{x}) g(x)=sin(x1)
前面两个例子说明的是左右极限存在,但左极限不等于右极限时双侧极限不存在,那有没有可能会出现左极限或右极限不存在的情况,有的 s i n ( 1 x ) sin(\frac{1}{x}) sin(x1) 就是这样的。
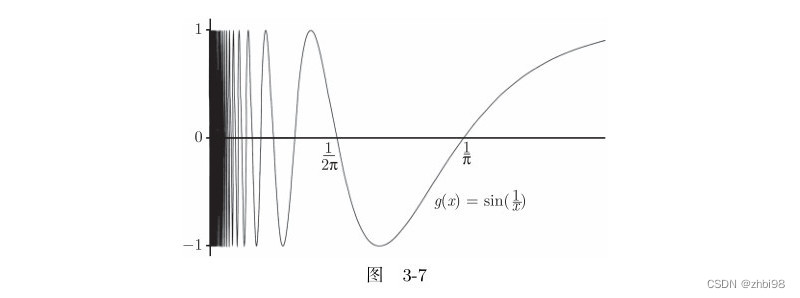
现在分析一下图像,由于 s i n ( x ) sin(x) sin(x) 在 x = π x=\pi x=π, 2 π 2\pi 2π, 3 π 3\pi 3π, . . . ... ... 上的值全为 0 0 0,所以 s i n ( 1 x ) sin(\frac{1}{x}) sin(x1) 会在 x = 1 π x=\frac{1}{\pi} x=π1, 1 2 π \frac{1}{2\pi} 2π1, 1 3 π \frac{1}{3\pi} 3π1, . . . ... ... 上的值全为 0 0 0。而 1 π \frac{1}{\pi} π1, 1 2 π \frac{1}{2\pi} 2π1, 1 3 π \frac{1}{3\pi} 3π1, . . . ... ... 这些数就是 s i n ( 1 / x ) sin (1/x) sin(1/x) 函数在 x x x 轴的值。
lim x → 0 + s i n ( 1 x ) \lim_{x\rightarrow0+}sin(\frac{1}{x}) limx→0+sin(x1) 是什么呢?以上图像在 x = 0 x=0 x=0 附近很杂乱,它无限地在 1 1 1
和 − 1 −1 −1 之间振荡,震荡的原因是随着 x x x 值得变化 s i n ( 1 x ) sin(\frac{1}{x}) sin(x1) 不断产生最小 − 1 -1 −1 到最大 1 1 1 之间含有小数的值(不是说只产生 -1 或 1,而是两者之间的实数值),当你从右侧向 x = 0 x=0 x=0 处移动时,振荡会越来越快,这里没有极限。
当 x x x 从右侧趋于 x = 0 x=0 x=0 时, s i n ( 1 x ) sin(\frac{1}{x}) sin(x1) 函数不趋于任何数,因此可以说 lim x → 0 + s i n ( 1 x ) \lim_{x\rightarrow0+}sin(\frac{1}{x}) limx→0+sin(x1) 不存在(即 D N E DNE DNE)。