在机器人建模中，D-H参数、旋量代数、李群、李代数和微分流形方法为机器人运动学和动力学的精确描述提供了理论基础。旋量代数、李群李代数和微分流形"均属于"PoE （Product of Exponentials）表示方法"的范畴。
D-H 表示方法和 PoE 表示方法的本质区别在于表述形式的不同。单纯就理解上来说，D-H 表示方法更加直接，其表现为"齐次变换矩阵"的乘积；PoE 表示方法则表现为"矩阵指数"的乘积。
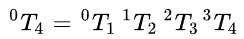
旋量坐标：
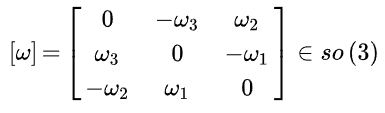
- D-H参数（Denavit-Hartenberg参数） ：
- D-H参数是一种用于描述机器人连杆和关节之间相对位置和姿态的方法。
- 它通过四个参数（连杆长度a、连杆扭角α、关节距离d、关节角度θ）来定义相邻连杆之间的空间关系。
- D-H表示方法更加直接，表现为"齐次变换矩阵"的乘积，从而建立了机器人各连杆之间的坐标变换关系。
- 旋量代数 ：
- 旋量代数是一种用于描述刚体空间运动的数学工具。
- 它将刚体的角速度和速度表示为旋量形式，旋量对应着刚体角速度和速度，可以写成向量形式。
- 在机器人建模中，旋量代数用于描述机械臂等刚体在空间中的运动轨迹和姿态变化。
- 李群（Lie Group） ：
- 李群是具有群结构的光滑微分流形，用于表征刚体坐标变换。
- 在机器人学中，常用的李群包括SO(3)（特殊正交群，描述三维旋转）和SE(3)（特殊欧几里得群，描述三维旋转和平移）。
- 李群通过指数映射与李代数相联系，为机器人运动学和动力学提供了丰富的数学工具。
- 李代数（Lie Algebra） ：
- 李代数是李群对时间的微分，表征刚体运动的速度。
- 对于SO(3)和SE(3)对应的李代数分别为so(3)和se(3)。
- 李代数在机器人位姿变换和轨迹规划中具有重要作用，可以方便地描述机器人的运动速度和加速度。
- 微分流形 ：
- 微分流形是现代微分几何中的一个基本概念，用于描述具有局部欧几里得性质的拓扑空间。
- 在机器人建模中，微分流形通常与李群和李代数一起使用，为机器人运动学和动力学的分析提供了强大的数学工具。
机器人建模方法中，D-H参数、旋量代数、李群、李代数和微分流形的方法对比，本质区别在哪，优劣程度如何？
https://www.zhihu.com/tardis/bd/ans/1984881689