DP读书：《材料科学基础》ALL复习考点

材料科学基础-知识点

老师说，这回期末考试90%考这个，我就整理

材料科学基础难点-第五章（相图）

杠杆定律

根据相律，二元系统两相平衡共存时自由度f=1，若温度确定，自由度f=0，说明在此温度下，两个平衡相的成分也随之而定。

通过合金在t温度的表象点，作水平线，水平线与液相线、固相线分别交于a、b两点（图5-13），点a、b在成分轴上的投影点20%，及w0%，即为此温度下液相（L）及固相（a）的成分（Ni 在液相、固相中的质量分数）。

设合金的总质量 Q Q Q。t温度时液相的质量为 Q L Q_L QL，固相~的质量为 Q a Q_a Qa。液、固两相的质量和应等于合金的总质量Q。

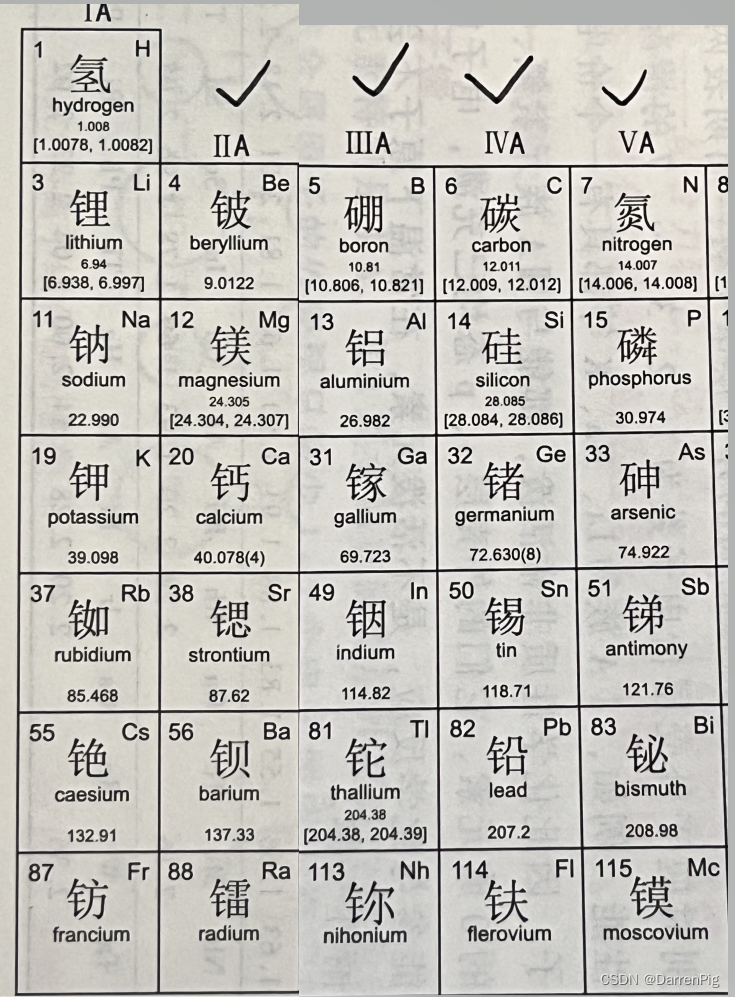
第三节二元系相图

本节重点讨论二元系合金的匀晶相图、其晶相、包晶相图以及具有重要应用价值的Fe-FesC 相图。对于其他类型的相图只作简单介绍。

一、匀晶相图及固溶体的结晶

一、匀晶相图

从液相中直接结晶出固溶体的反应称为匀晶反应。只发生匀晶反应的相图称为匀晶相图。匀晶相图中的两组元在液态、固态都无限互溶。具有这类相图的二元合金系有 C u − N i 、 A g − A u 、 A g − P t 、 F e − N i 、 C u − A u 、 G r − M o Cu-Ni、Ag-Au、Ag-Pt、Fe-Ni、Cu-Au、Gr-Mo Cu−Ni、Ag−Au、Ag−Pt、Fe−Ni、Cu−Au、Gr−Mo等。有些硅酸盐材料如镁橄榄石（Mg2SiO4）-铁橄榄石（FezSiO4）等也具有此类特征。

2. 固溶体的平衡结晶过程

平衡结晶过程是指在极缓慢的冷却过程中，每个阶段都能达到平衡的结晶过程。下面以Cu-Ni 相图为例进行分析。

取合金成分为0（图5-18），0点成分的合金自液态缓慢冷却，当温度降至t」时，直线00'与液相线交于a，表示结晶开始。从图中可以看出，在此温度结晶出的固相成分应为a。运用杠杆定律可以求得，此时固相质量分数为零，说明实际固相并未形成。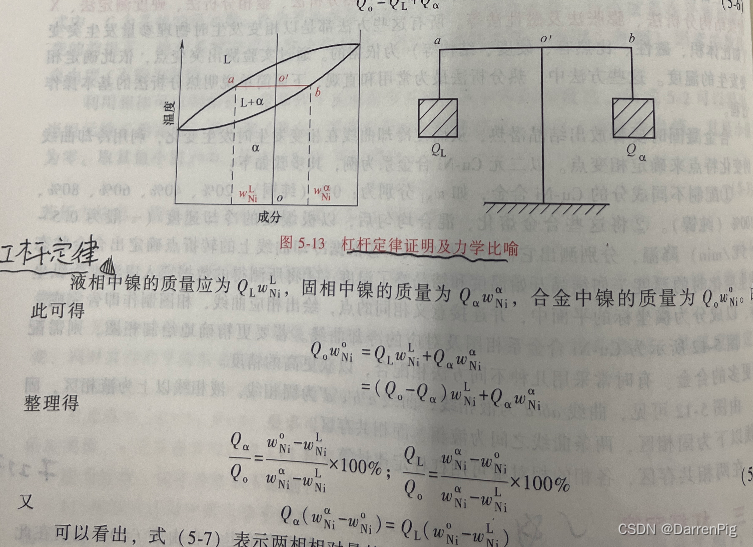降至b，已有一定质量的固相结晶。此温度下液相、固相的平衡成分分别为 C L C_L CL，与 G o G_o Go，用杠杆定律可算出两相相对量为温度降至"3时，00'线与固相线交于63点，结晶过程完成。此时已结晶出的固相成分与合金成分完全相同，说明液相通过此过程已完全转变为成分均匀的单相固溶体。

此结晶过程也可用如下方式表述：

平衡结晶过程分析

c 复制代码

从以上结晶过程可以看出，固溶体与纯金属结晶的不同之处是：

1）固溶体结晶是在一个温度范围内完成的，而纯金属结晶是在恒温下完成的（f=0）。
2）合金结晶过程中，结晶出的固相与共存液相的成分不同，这种结晶称为选分结晶。
> 选分结晶过程中，为了满足不同温度下两相平衡共存的成分要求，不同温度下，液相成分沿液相线>发生变化，同时固相成分沿固相线发生变化。
> 成分的变化、调整，是靠Cu、Ni 原子的扩散来完成的。而纯金属在结晶过程中，固相与液相的成分始终是相同的。

3. 匀晶系的不平衡结晶

由上述平衡结晶过程的分析可知，结晶过程中的每一阶段，液相与固相都必须满足所处温度下的平衡成分，而这一条件的实现，是靠液相与固相中原子的充分扩散 来完成的。这一过程进行的极为级慢，需要足够长的时间。然而，在实际生产中，液态合金强 23-32人型腔后，冷却速度比较快，达到某一温度时，扩散过程尚未来得及充分进行温度已继含全週图续下降，所以不可能按照相图所指示的温度和成分的平衡变化规律进行。此过程称为不平衡凝固过程。

下面以图5-19 说明不平衡结晶过程。一般而言，原子在液态中的扩散速度远大于在固高冲的扩散速度，因此可以假定在不平偷凝圖过程中，原子在液相中能充分扩散，并使液相完全均匀，原子来不及在固相中扩散。

二、共晶相图及其结晶

两组元在液态无限互溶 ，固态有限互溶或完全不互溶，且冷却过程中发图，称为共晶相图（图5-24），具有共晶相图的合金系有 P b − S n 、 P b − S b 、 A I B i Pb-Sn、Pb-Sb、AIBi Pb−Sn、Pb−Sb、AIBi 等。一些硅酸盐也具有共晶相图。

下面以Pb-Sn 合金系的二元共晶相图为例，对共晶相图及其合金的结晶

相图分析
图5-24日所示为 P b − S n Pb-Sn Pb−Sn二元共晶相图，图中ae、be 为液相线，am、bnSn 在Pb中的固溶度曲线，同样ng 为Pb 在Sn 中的固溶度曲线。
图中有三个单相区：液相区L、固相A相区及固相B 相区 。从图中可2b中的固溶体，B相是Pb 在Sn 中的固溶体。三个两相区：L+a、L+B及a+B

只要将描述记下就好

三、包晶系合金相图

在实际情况下，液体和固体中的原子扩散都是不充分的。α相生长时，由于界面前成分过冷，一般都以枝晶状生长，在生长时还存在着晶内偏析。真正的包晶转变仅产生于α和液体直接接触时。a+L→β产生的β相在α 树枝表面的析出也有一个生核和生长过程。如果β相与α相之间存在较好的界面共格关系，β相容易以α表面作为衬底而生核析出。对一系列包晶合金的考查表明，许多包晶系中α和B之间存在着良好的界面共格关系，例如Fe-C系中的δ和γ相，Al-Ti系中的TiAl3和α之间等等。β可以在一个α枝晶表面的许多部位进行生核，它们在生长过程中逐渐合并在一起，但有的晶核在生长过程中可能产生位向的偏移或在生长界面前沿出现杂质的富集，它们与从邻近晶核长出的晶体间出现晶界，于是一个α枝晶上可能生长出几个β晶体，好像β晶粒把原有的α枝晶分割成几部分，这种现象称为粒化

材料科学基础（一、二、四）复习考点

1.原子可以看成由原子核 及分布在原子核周围的电子所组成。原子核内有中子和质子，原子核的体积很小，却集中了原子的绝大部分质量。电子绕着原子核在一定的轨道上旋转，它们的质量虽可忽略 ，但电子的分布 却是原子结中最重要的因素，它不仅决定了单个原子的行为，也对工程材料内部原子的结合以及材料的某些性能起着决定性作用，本节介绍的原子结构主要指电子的排列方式。

泡利不相容原理最低能量原理四个量子数

1. 原子核外电子的分布与四个量子数有关，且服从下述两个基本原理:
- 泡利不相容原理 一个原子中不可能存在四个量子数完全相同的两个电子
  最低能量原理 电子总是优先占据能量低的轨道，使系统处于最低的能量状态
1. 通常把材料的液态和固态 称为凝聚态
1. 结合力的强弱可把结合键 分成两大类:
  - 一次键 结合力较强，包括离子键、共价键和金属键
  - 二次键 结合力较弱，包括范德瓦耳斯键和氢键
1. 离子键
  
  金属元素特别是IA、IA 族金属 在满壳层外面有少数价电子，它们很容易逸出;ⅣA、ⅦA 族的非金属原子 的外壳层只缺少 1~2 个电子便成为稳定的电子结构。当两类原子结合 时，金属原子的外层电子很可能转移至非金属原子外壳层上，使两者都得到稳定的电子结构，从而降低了体系的能量，此时金属原子和非金属原子分别形成正离子与负离子，正、负离子相互吸引，使原子结合在一起，这就是离子键。
1. 共价键
  
  价电子数为4或5个的IVA、VA族 元素，相邻原子间可以共同组成一个新的电子轨道，两个原子中各有一个电子共用，利用共享电子对来达到稳定的电子结构，这就是共价键。
1. 金属键
  
  金属键正是依靠正离子与自由电子之间的相互吸引而结合起来的
1. 二次键
  
  不是依靠电子的转移或共享，而是借原子之间的偶极吸引力结合而成，这就是二次键。
1. 氢键
  
  也是靠原子(或分子、原子团) 的偶极吸引力 结合，只是氢键中氢原子起了关键作用
  
  氢原子更在两个电负性很强的原子(或原子团)之间形成一个桥梁
1. 结合键与性能：物理性能化学性能力学性能---【第一章结束】
1. 晶体结构 = 空间点阵+原子+离子+分子
  
  （晶体结构 = 空间点阵+基元）
1. 立方、四方、正交
1. 空间点阵中各阵点排列的方向排列的方向，称为晶向。通过空间点阵中任意一组的平面代表晶体中的原子平面，称为晶面。【画图题】
1. 配位数：在离子晶体中，与某一考察离子邻接的异号离子的数目称为该考察离子的配位数
1. 晶体材料分为金属晶体、离子晶体、共价晶体和分子晶体，这些晶体中的原子靠不同的化学键结合在一起。
- 根据原子的化学键的不同晶体材料分为:金属晶体、离子晶体、共价晶体和分子晶体
1. 共价晶体的特点：强度高、硬度大、脆性大、熔点高、沸点高、挥发性低、导电能力较差和结构稳定等特性。
1. 空位：如果晶体中某结点上原子空缺 ，则可以形成空穴（空位）
1. 晶体缺陷：分为三大类
- 点缺陷
- 线缺陷
- 面缺陷
1. 过饱和点缺陷 的产生：晶体中点缺陷的数目 明显超过平衡值，称这些点缺陷
1. 位错对晶体的扩散和相变等过程具有一定的影响
1. 柏氏矢量 ：位错区原子的畸变特征表示，包括畸变发生在什么晶向以及畸变大小
- 柏氏模量（螺旋位错的）与位错线平行；
（刃形位错）与位错线垂直
1. 位错的攀移，位错的本质是刃形位错的半原子面向上或向下移动，攀移时位错线的运动反向垂直于柏氏矢量。
1. 位错的观察：
- 浸蚀技术
- 投射电子显微镜
1. 晶界能：原子或多或少的偏离了平衡位置，所以相对于晶体内部的晶界处于较高的能量状态，高出的那部能量称为晶界能。
1. 表面及表面能 ：
1. 固体表面的吸附按其作用力的性质可以分为两大类：物理吸附、化学吸附
1. 润湿行为：观察液体表面之间的接触角ɵ（或称润湿角）
1. 晶体中的面缺陷 有晶界、相界、表面等。根据晶界两侧的位向差可把晶界分为小角度晶界和大角度晶界。
1. 【第六章】...

### 材料科学基础：计算题（第6章）

一、结晶驱动力与过冷度的计算

以下为必考计算题

∆ G < 0 ; G = H − T S ∆G<0; G=H-TS ∆G<0;G=H−TS

d G d T = d H d T − S − T d S d T \frac{dG}{dT}=\frac{dH}{dT}-S-T\frac{dS}{dT} dTdG=dTdH−S−TdTdS

d G d T = d H d T − S − d Q d T \frac{dG}{dT}=\frac{dH}{dT}-S-\frac{dQ}{dT} dTdG=dTdH−S−dTdQ

又 d H = d Q dH=dQ dH=dQ 有
d G d T = − S \frac{dG}{dT}=-S dTdG=−S

液相自由能与与固相自由能相等，

当熔点低于 T m Tm Tm 时, G S < G L G_S<G_L GS<GL 液态才能自发的转为固相。

∆ G V ∆G_V ∆GV越大，过冷度越大，凝固的驱动力也就越大

二、液体金属在凝固时的计算

题目、液体金属在凝固时必须过冷，而在加热使其格化却毋需过热，即一旦加热到熔点就立即熔化，为什么?

今给出一组典型数据作参考:

以金为例，其 Y S L = 0.132 , Y L V = 1.128 , Y S V = 1.400 Y_{SL}=0.132,Y_{LV}=1.128,Y_{SV}=1.400 YSL=0.132,YLV=1.128,YSV=1.400分别为液固、液气、固气相的界面能 ( 单位 J / m J/m J/m )

液体金属在凝固时必须克服表面能，形核时自由能变化大于零，故需要过冷。

固态金属熔化时，液相若与气相接触，当有少量液体金属在固相表面形成时，就会很快覆盖在整个表面(因为液体金属总是润湿同一种固体金属)

由于熔化时， ∆ G V = 0 ∆G_V=0 ∆GV=0，所以 ∆ G = ∆ G V + ∆ G 表面 ∆G=∆G_V+∆G_{表面} ∆G=∆GV+∆G表面，

因为液体金属总是润湿同一种固体金属，

即表面能变化决定过程能否自发进行

实验指出: Y S V = 1.4 > Y S L + Y L V = 0.132 + 1.128 = 1.260 Y_{SV}=1.4>Y_{SL}+Y_{LV}=0.132+1.128=1.260 YSV=1.4>YSL+YLV=0.132+1.128=1.260，说明在熔化时，表面自由能的变化 ∆ G 表面 < 0 ∆G_{表面}<0 ∆G表面<0，即不存在表面能障碍，也就不必过热