C. Rooks Defenders（树状数组）

You have a square chessboard of size n×nn×n. Rows are numbered from top to bottom with numbers from 11 to nn, and columns --- from left to right with numbers from 11 to nn. So, each cell is denoted with pair of integers (x,y)(x,y) (1≤x,y≤n1≤x,y≤n), where xx is a row number and yy is a column number.

You have to perform qq queries of three types:

Put a new rook in cell (x,y)(x,y).
Remove a rook from cell (x,y)(x,y). It's guaranteed that the rook was put in this cell before.
Check if each cell of subrectangle (x1,y1)−(x2,y2)(x1,y1)−(x2,y2) of the board is attacked by at least one rook.

Subrectangle is a set of cells (x,y)(x,y) such that for each cell two conditions are satisfied: x1≤x≤x2x1≤x≤x2 and y1≤y≤y2y1≤y≤y2.

Recall that cell (a,b)(a,b) is attacked by a rook placed in cell (c,d)(c,d) if either a=ca=c or b=db=d. In particular, the cell containing a rook is attacked by this rook.

Input

The first line contains two integers nn and qq (1≤n≤1051≤n≤105, 1≤q≤2⋅1051≤q≤2⋅105) --- the size of the chessboard and the number of queries, respectively.

Each of the following qq lines contains description of a query. Description begins with integer tt (t∈{1,2,3}t∈{1,2,3}) which denotes type of a query:

If t=1t=1, two integers xx and yy follows (1≤x,y≤n1≤x,y≤n) --- coordinated of the cell where the new rook should be put in. It's guaranteed that there is no rook in the cell (x,y)(x,y) at the moment of the given query.
If t=2t=2, two integers xx and yy follows (1≤x,y≤n1≤x,y≤n) --- coordinates of the cell to remove a rook from. It's guaranteed that there is a rook in the cell (x,y)(x,y) at the moment of the given query.
If t=3t=3, four integers x1,y1,x2x1,y1,x2 and y2y2 follows (1≤x1≤x2≤n1≤x1≤x2≤n, 1≤y1≤y2≤n1≤y1≤y2≤n) --- subrectangle to check if each cell of it is attacked by at least one rook.

It's guaranteed that among qq queries there is at least one query of the third type.

Output

Print the answer for each query of the third type in a separate line. Print "Yes" (without quotes) if each cell of the subrectangle is attacked by at least one rook.

Otherwise print "No" (without quotes).

Example

input

Copy

复制代码

output

Copy

复制代码

No
Yes
Yes
No
Yes

Note

Consider example. After the first two queries the board will look like the following picture (the letter RR denotes cells in which rooks are located, the subrectangle of the query of the third type is highlighted in green):

Chessboard after performing the third and the fourth queries:

正在上传...重新上传取消正在上传...重新上传取消

Chessboard after performing the fifth and the sixth queries:

正在上传...重新上传取消正在上传...重新上传取消

Chessboard after performing the seventh and the eighth queries:

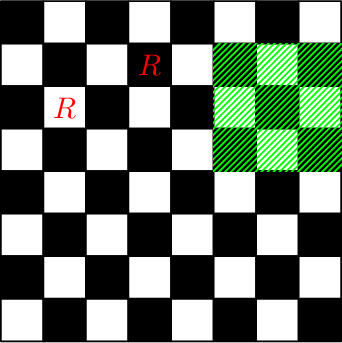
Chessboard after performing the last two queries:

正在上传...重新上传取消正在上传...重新上传取消

思路：

1，能不能撞击的关键在于行列是否出现过

2，用前缀和和差分来实现

代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
const int maxj=2e5+100,mod=1e9+7,inf=0x7f7f7f7f7f7f7f7f;
template<class t> void read(t &res){
    char c;t flag=1;
    while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;res=c-'0';
    while((c=getchar())>='0'&&c<='9')res+=c-'0';res*=flag;
}
int n,q;
int sum1[maxj],sum2[maxj];
struct bit{
    int lowbit(int x){return x&-x;}
    void add(int x,int c,int sum[]){while(x <= n)sum[x]+=c,x+=lowbit(x);}
    int getsum(int x,int sum[]){int res=0;while(x)res+=sum[x],x-=lowbit(x);return res;}
}t;
int x[maxj],y[maxj];
void solve(){  //对行列做标记
    cin>>n>>q;
    while(q--){
        int v;
        cin>>v;
        if(v==1){
            int l,r;
            cin>>l>>r;
            x[l]++;y[r]++;
            if(x[l]==1)t.add(l,1,sum1);//可多次放，多次拿
            if(y[r]==1)t.add(r,1,sum2);
        }else if(v==2){
            int l,r;
            cin>>l>>r;
            x[l]--;y[r]--;
            if(x[l]==0)t.add(l,-1,sum1);
            if(y[r]==0)t.add(r,-1,sum2);
        }else{
            int l,r,ll,rr;
            cin>>l>>r>>ll>>rr;
            if(t.getsum(ll,sum1)-t.getsum(l-1,sum1)==ll-l+1||t.getsum(rr,sum2)-t.getsum(r-1,sum2)==rr-r+1)
                cout<<"Yes"<<'\n';
            else 
                cout<<"No"<<'\n';
        }
    }
}
int32_t main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#ifdef LOCAL
    freopen("input.txt", "r", stdin);
    freopen("output.txt", "w", stdout);//a为add
#endif
    int t;
    t=1;
    while(t--)solve();
    return 0;
}