高精度乘法

思路
题目

本篇计算的是高精度整数乘以一个较小的整数。（都是非负的，负数只需要稍作加工即可）

高精度数指的是一个非常非常大的数字，一般的整型数据类型存不下它的值。

思路

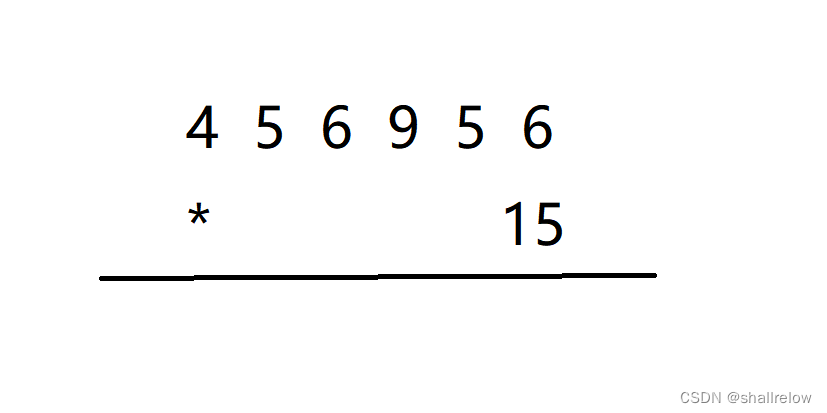
高精度乘法当中的代码计算方式与我们现实生活中自己做乘法时不太一样。

对于这个题目，首先会先计算 6 * 15，然后进 9。

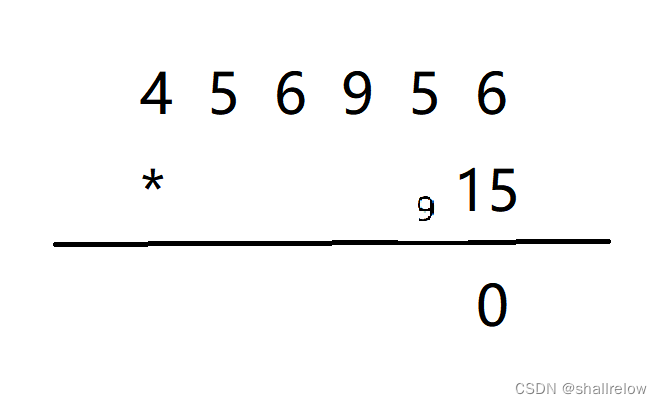
接着计算 5 * 15，答案是75，加上刚才的进位9，就是84。

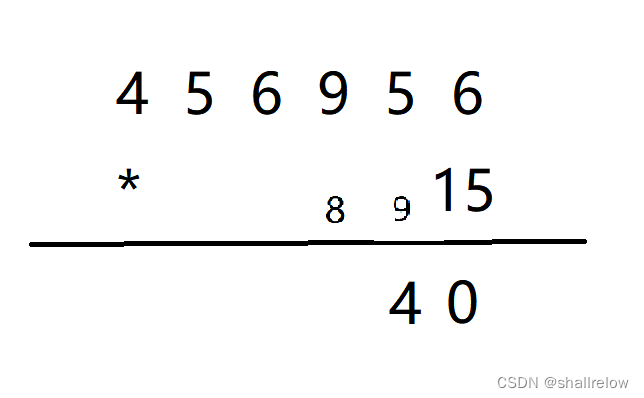
以此类推。

而平时我们计算乘法，都是先计算 5 * 456956 然后加上 10 * 456956。

接着来看代码的实现。

题目

给定两个非负整数（不含前导 0 0 0） A A A 和 B B B，请你计算 A × B A \times B A×B 的值。

输入格式

共两行，第一行包含整数 A A A，第二行包含整数 B B B。

输出格式

共一行，包含 A × B A \times B A×B 的值。

数据范围

1 ≤ A 的长度 ≤ 100000 1 \le A 的长度 \le 100000 1≤A的长度≤100000,
0 ≤ B ≤ 10000 0 \le B \le 10000 0≤B≤10000

输入样例：

2
3

输出样例：

首先是准备阶段：

接着跟高精度加法和减法当时的操作一样，倒着存储在vector容器中。

这里需要注意的是，题目当中的 b是可能为 0的，所以需要特判一下。

接着把高精度乘法封装成一个函数，然后用变量C接收，最后倒着遍历打印一遍 C。

mul函数的外壳长这个样子。

首先定义一个返回的vector容器C。

高精度加法和高精度乘法比较像，都需要定义一个进位。

这个 t 的含义就是就是上一位的进位。

接着遍历整个数字。

根据之前的思路，接下来让 t 加上此时A的这一位乘以 b.

此时 t 的个位就是这一位的结果。

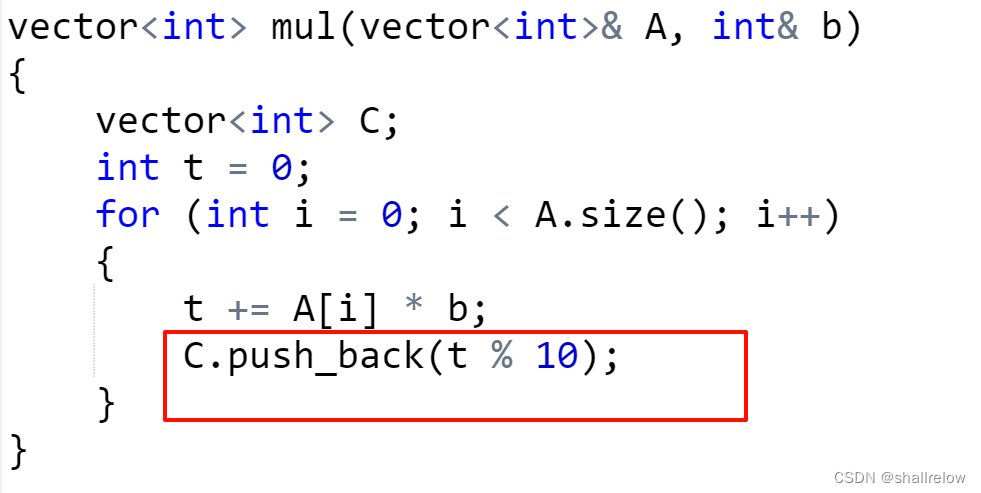
接着再更新新的进位，只需要让 t /= 10即可。

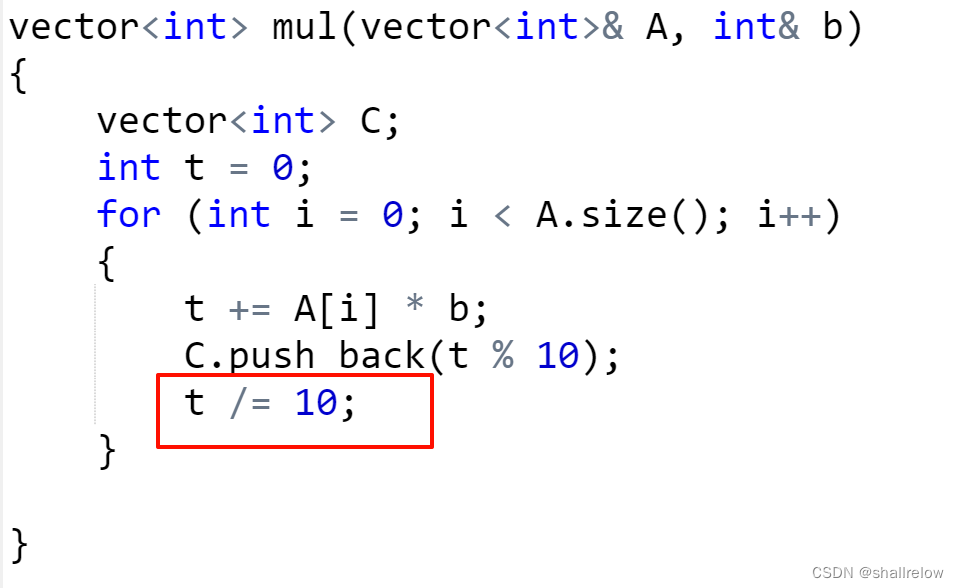
跟高精度加法一样，最高位有可能会再次进位，而我们只遍历到了最高位，所以最后还需要插入进位，当然前提是不等于0.

最后返回我们的 vector容器C 即可。

完整代码：

cpp 复制代码

#include <iostream>
using namespace std;
#include <vector>

string a;
int b;
vector<int> A;

vector<int> mul(vector<int>& A, int& b)
{
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i++)
    {
        t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }
    if (t) C.push_back(t);
    return C;
}

int main()
{
    cin >> a >> b;
    if (b == 0)
    {
        cout << "0";
        return 0;
    }
    for (int i = a.size()-1; i >= 0; i--) A.push_back(a[i] - '0');
    
    auto C = mul(A, b);
    for (int i = C.size()-1; i >= 0; i--) cout << C[i];
    
    return 0;
}

完