使用高斯混合模型（GMM）进行猫狗音频聚类（Kaggle Audio Cats and Dogs）

Audio Cats and Dogs | Kaggle

一、实验目标

二、数据分析

三、实验结果

四、改进方向

一、实验目标

数据集包括164个标注为猫的.wav文件，总共1323秒和113个标注为狗叫声的.wav文件，总共598秒，要求判别每个音频是狗叫还是猫叫

二、数据分析

随机播放了一些音频，然后使用下面的代码输出了他们的声谱图、频率随时间变化和梅尔倒频率系数的热力图：

python 复制代码

# 读取音频文件
Audio = np.array(librosa.load('./cats_dogs/cat_86.wav')[0])
SampleRate=librosa.load('./cats_dogs/cat_86.wav')[1]
# 绘制声谱图
plt.plot(Audio)
plt.show()
#绘制频率随时间变化的波形图
plt.specgram(Audio, Fs = SampleRate)
plt.show()
#绘制梅尔频率倒谱系数热图
MFCC = librosa.feature.mfcc(y = Audio, sr = SampleRate)
plt.imshow(MFCC, cmap = 'hot')
plt.show()

发现一些音频10秒左右的长度中只有不到3秒的动物叫声，其他都是一些杂音，在6s左右的地方还是能看出来猫的声音特征的：

cat_1.wav：

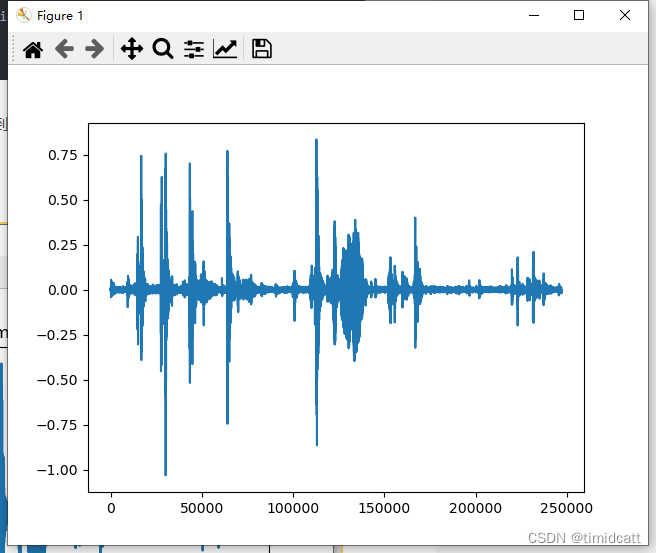
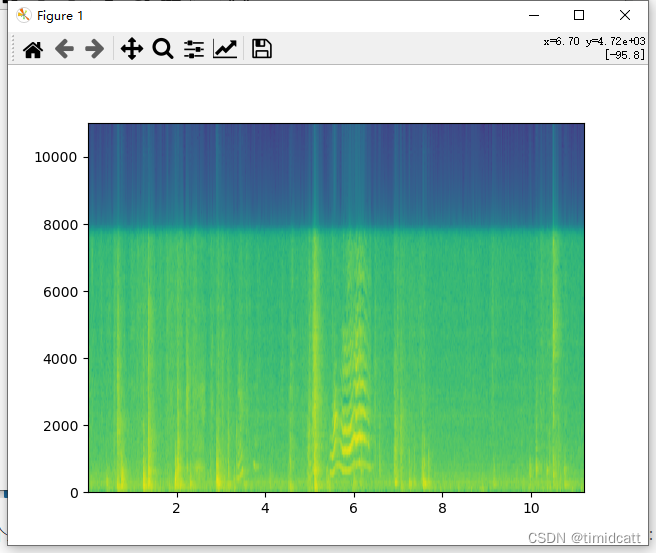
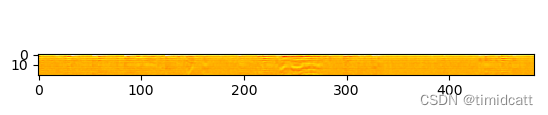
有一些音频是没有动物叫声的，只有杂音，从频率图可以看出没有猫的特征：

cat_41.wav

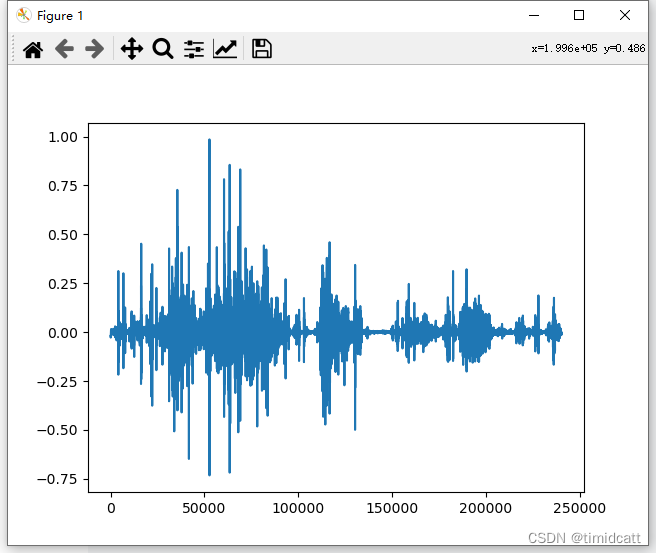
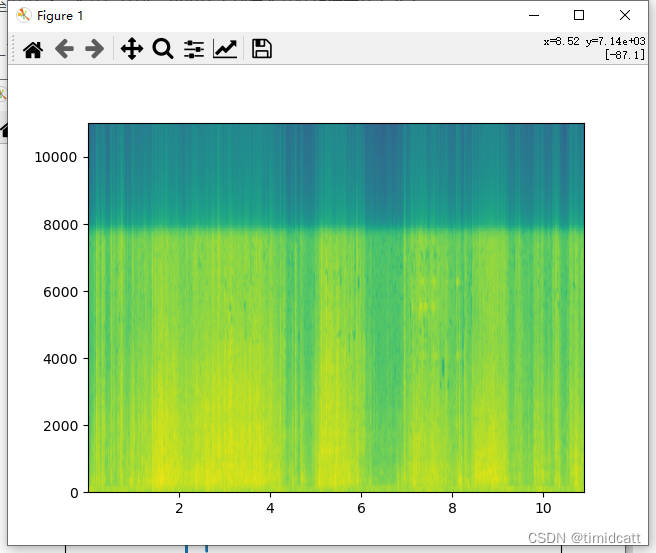
还发现了一个音乐片段，也是与猫的特征完全不同：

cat_123.wav：

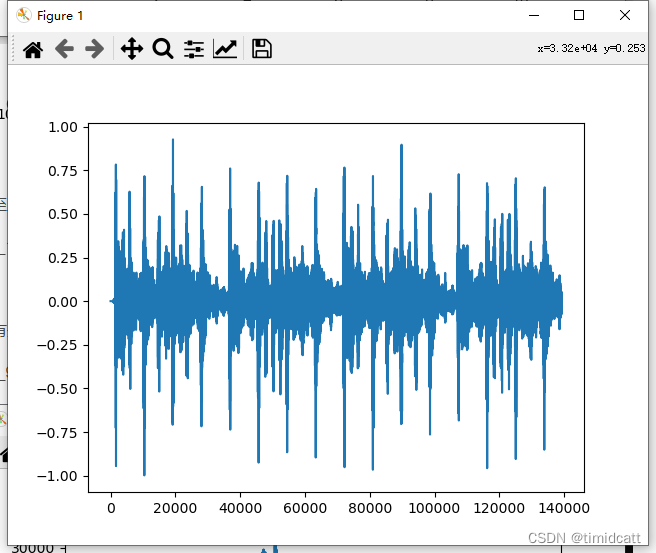
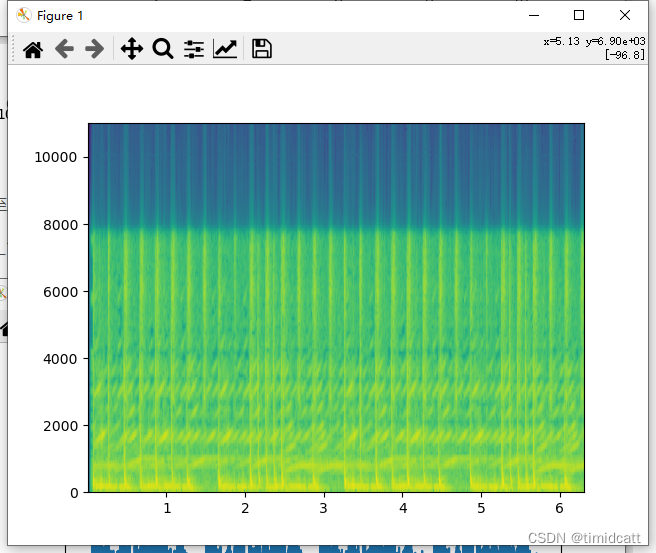
也有最容易辨别的，只有叫声的音频，猫的特征最为明显：

cat_9.wav

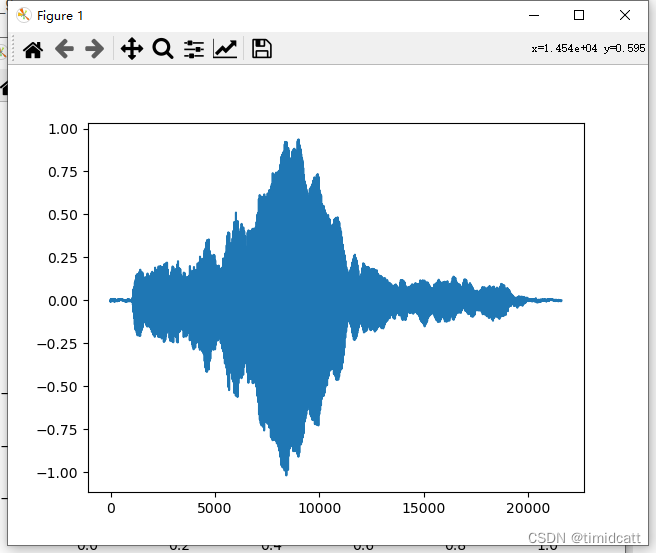
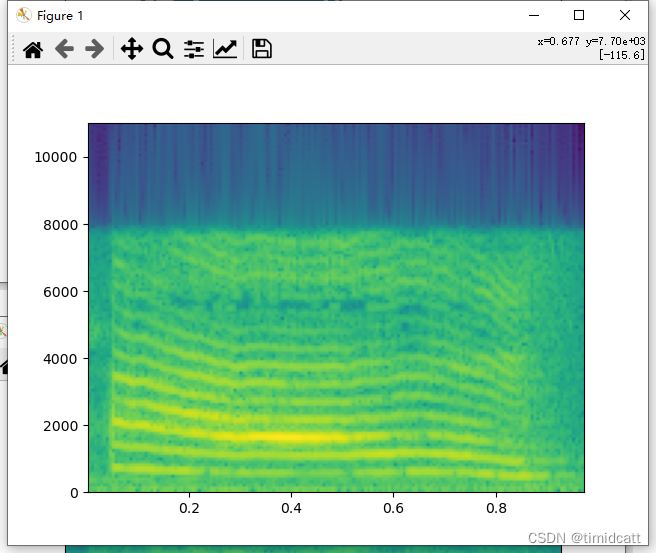
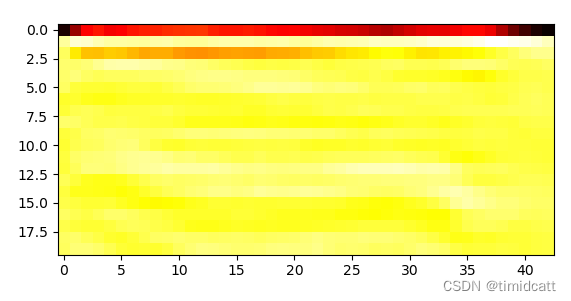
狗叫声听上去大部分都比较正常(不过也发现有像dog_barking_108.wav是杂音)

dog_barking_39.wav:

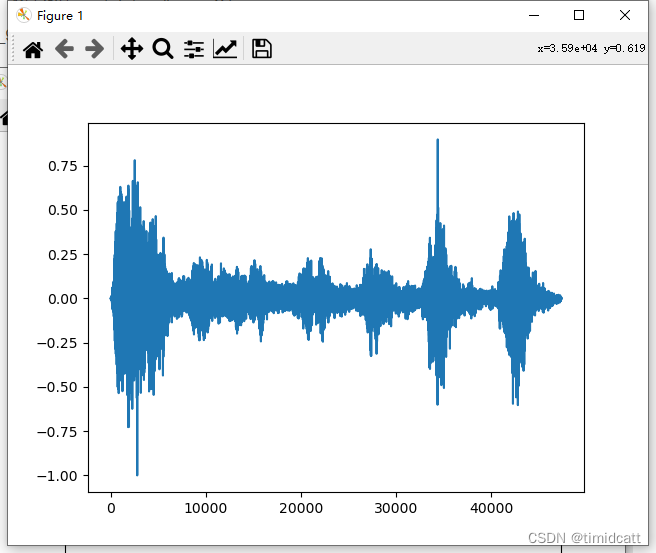
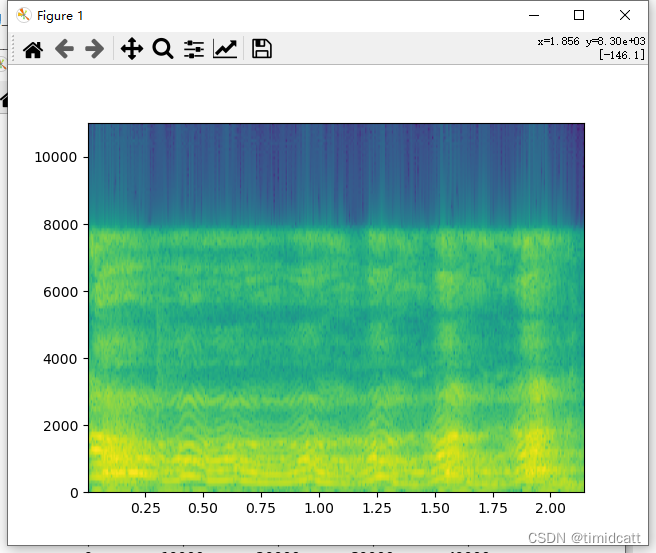
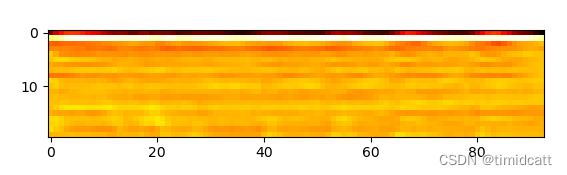
其他的音频就不过多展示了，可以看出猫叫声的频率在2000及以上最高，狗叫声频率分布在2000以下，猫叫声的MFCC热力图颜色浅，而狗的热力图颜色深

三、实验结果

我们这里选择了差距看上去更大一点的MFCC作为音频特征，更准确的说是MFCC均值,构建高斯混合模型，并使用期望最大化算法进行训练，代码如下：

python 复制代码

#音频特征
Features = []
#音频标签
Labels = []
#遍历277个音频文件
for File in os.listdir("./cats_dogs"):
    #获取音频时间序列和采样率 
     y, sr = librosa.load("./cats_dogs/"+File)
     #计算音频的MFCC
     #MFCC的计算过程通常包括以下几个步骤：对原始信号进行傅里叶变换，以将其从时域转换到频域；接着将线性频率尺度转换为梅尔频率尺度；然后通常取其对数并施加离散余弦变换（DCT），最终得到倒谱系数。
     MFCC = librosa.feature.mfcc(y=y, sr=sr,n_mfcc=100)
     #计算MFCC的平均值作为特征
     Features.append(np.mean(MFCC, axis=1))
     if File[0]=='c':
         Labels.append(0)
     else:
         Labels.append(1)

Features=np.array(Features)
Labels=np.array(Labels)
#构建高斯混合模型
GMM=GaussianMixture(n_components=2,covariance_type='full',tol=1e-3,reg_covar=0.000001,max_iter=100)
#通过期望最大化算法对模型进行聚类并预测
GMM.fit(Features)
Predictions = GMM.predict(Features)
#输出测试的准确率
Accuracy = accuracy_score(Labels, Predictions)
print(confusion_matrix(Labels,Predictions))
print("Accuracy:", Accuracy)

跑出来的最好结果：

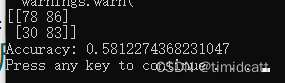
通过混淆矩阵可以看出，狗的正确率达到了73%，而猫的正确率只有47%，应该和数据集有关，狗的相关音频质量比猫要高一些

四、改进方向

要提高正确率，首先可以对数据进行清晰，包括对音频中无关部分进行裁剪，去除无关音频，具体清洗方法可以从频率图入手

其次可以对GMM模型进行调参，以及尝试使用频率作为特征等