


2713.矩阵中严格递增的单元格数【困难】
题目:
给你一个下标从 1 开始、大小为 m x n 的整数矩阵 mat,你可以选择任一单元格作为 起始单元格 。
从起始单元格出发,你可以移动到 同一行或同一列 中的任何其他单元格,但前提是目标单元格的值严格大于当前单元格的值。
你可以多次重复这一过程,从一个单元格移动到另一个单元格,直到无法再进行任何移动。
请你找出从某个单元开始访问矩阵所能访问的 单元格的最大数量 。
返回一个表示可访问单元格最大数量的整数。
示例 1:
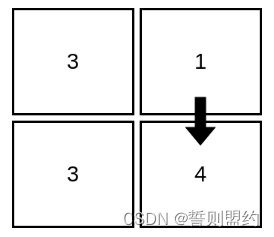
输入:mat = [[3,1],[3,4]]
输出:2
解释:上图展示了从第 1 行、第 2 列的单元格开始,可以访问 2 个单元格。可以证明,无论从哪个单元格开始,最多只能访问 2 个单元格,因此答案是 2 。 示例 2:
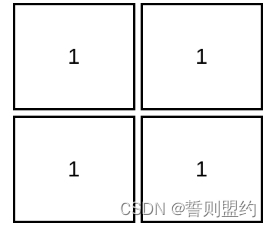
输入:mat = [[1,1],[1,1]]
输出:1
解释:由于目标单元格必须严格大于当前单元格,在本示例中只能访问 1 个单元格。示例 3:
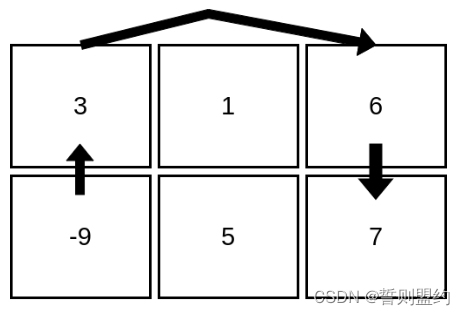
输入:mat = [[3,1,6],[-9,5,7]]
输出:4
解释:上图展示了从第 2 行、第 1 列的单元格开始,可以访问 4 个单元格。可以证明,无论从哪个单元格开始,最多只能访问 4 个单元格,因此答案是 4 。分析问题:
这道题旨在寻找一个最大解,可以用动态规划来解,而题意又是让我们顺序移动单元格,只能从小到大的顺序,因此我们可以用一个哈希表来记录每个值所对应的坐标,遍历每个可能的起点。
在这个过程中,我们可以维护两个数组 rowMax 和 colMax,分别记录每一行和每一列的最大递增长度。初始时,这两个数组的所有元素都为 0。
对于每个值对应的所有单元格位置,我们按照位置顺序遍历,对于每个位置 (i,j),我们可以计算出以该位置为终点的最大递增长度为 1+max(rowMax[i],colMax[j]), 更新答案,然后更新 rowMax[i] 和 colMax[j]。

代码实现:
python
class Solution:
def maxIncreasingCells(self, mat: List[List[int]]) -> int:
M = len(mat)
N = len(mat[0])
# 建立一个哈希表
value_buckets = defaultdict(list)
for i in range(M):
for j in range(N):
value_buckets[mat[i][j]].append((i, j))
row_best = [0] * M
col_best = [0] * N
ans = 0
for val in sorted(value_buckets.keys()):
cells = value_buckets[val]
updates = []
for r, c in cells:
mx = 1 + max(row_best[r], col_best[c])
updates.append((r, c, mx))
ans = max(ans, mx)
for r, c, mx in updates:
row_best[r] = max(row_best[r], mx)
col_best[c] = max(col_best[c], mx)
return ans
总结:
代码详解:
首先,通过 len(mat) 和 len(mat[0]) 分别获取了输入矩阵 mat 的行数 M 和列数 N 。
然后,创建了一个默认字典 value_buckets 。在接下来的两层循环中,遍历矩阵 mat 的每个元素。对于每个元素的值,将其对应的坐标 (i, j) 添加到 value_buckets 中以该值为键的列表中。
接着,创建了两个列表 row_best 和 col_best ,分别用于记录每行和每列的最佳值,并初始化为全 0 。还初始化了一个变量 ans 用于保存最终的结果,并初始化为 0 。
之后,对 value_buckets 中的键(即矩阵中的值)进行排序。对于每个排序后的键值 val ,获取对应的坐标列表 cells 。然后创建一个空列表 updates 用于保存后续的更新信息。
在遍历 cells 中的每个坐标 (r, c) 时,计算当前位置能达到的最大值 mx ,它等于 1 加上 row_best[r] 和 col_best[c] 中的最大值。将 (r, c, mx) 添加到 updates 列表中,并更新 ans 为 ans 和 mx 中的最大值。
最后,再次遍历 updates 列表,更新 row_best[r] 和 col_best[c] 为它们自身和 mx 中的最大值。
最终,方法返回 ans ,即矩阵中按照特定规则能达到的最大结果值。
主要考查内容:
- 对二维列表的遍历和操作。
- 使用默认字典
defaultdict来根据值存储坐标。 - 对值进行排序,并基于排序后的结果进行一系列计算和更新操作。
- 维护两个分别记录每行和每列最佳值的列表
row_best和col_best。
通过这段代码可以学到:
- 如何有效地处理二维数组中的数据。
- 例如通过两层循环遍历二维数组的每个元素。
- 运用
defaultdict来根据特定的值组织数据。- 方便后续按照值的顺序进行处理。
- 结合排序和逐步更新的策略来解决复杂的最值问题。
- 通过比较和更新
row_best和col_best来获取最终的最大结果。
- 通过比较和更新
