今天鄙人为大家带来的是一道简单的逻辑运算题。用用到了一个我们在链表中提及过的方法快慢法。这道题其实没啥考的实际意义。只是我们如果能了解这道题的解决方法的话。对我们后面梳理逻辑会有很大的帮助。
单链表的题目
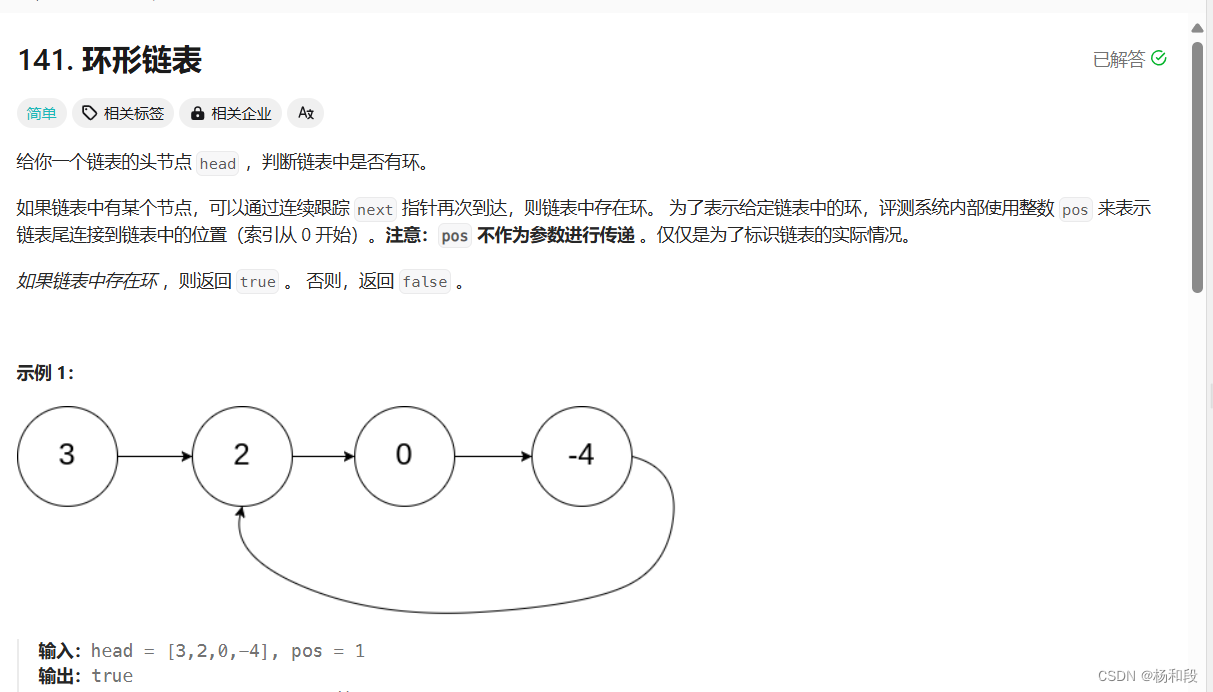
我们可以看到上面的题目。就是让我们判断是否带环。也许大家这样看起来可能不是很直观,那么我们重新画一个图,大家看着可能会更好一点。
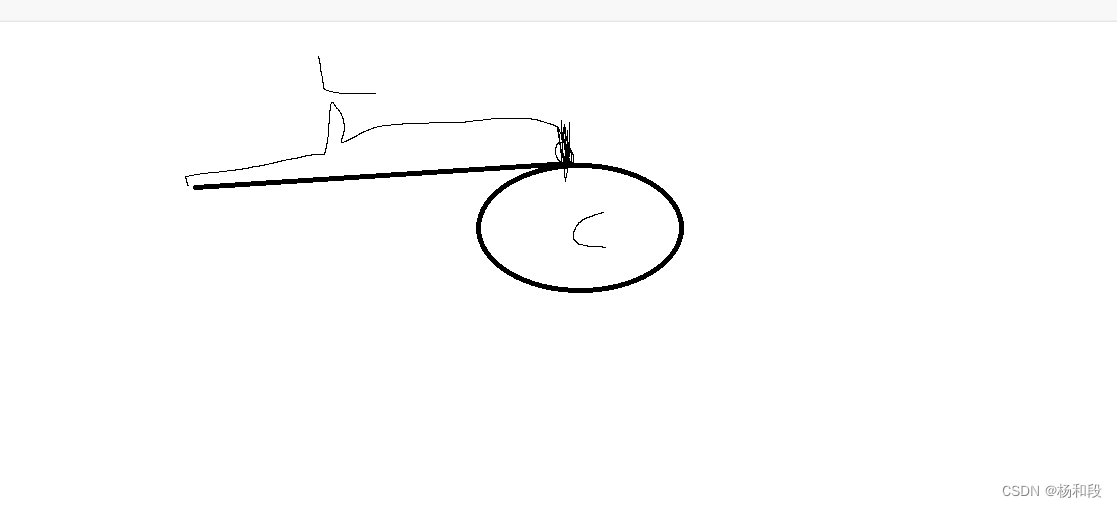
大家可以看到这个图里面给我表示的是这个链表没有进环的地步。然后有一个竖直的黑点,就是他们环相交的地方。那么我们只需要判断是否存在这么一个点,那么就是不是能够判断是否带环了。 那么我们如何来判断他们是否有这么个点呢?然后这就是我们开始在序言中说的快慢指针的方法了。那什么叫快慢指针呢?快慢指针就是一个快,一个慢慢。例如一个指针每次走一步,一个指针每次走两步。我们以这个图为例。当慢支撑走了我的一半的话,那么快指针就已经走到他们的相交点了(就是那个黑色柱子)。当慢指针走到那个焦交点的时候,快指针已经在c里面走了一段时间了。然后当慢指针继续往前走,快指针也快速走。那么这就变成了我们的追赶问题了。如果带环的话,那么快指针一定会追慢指针的,因为我比你快一步,那么相当于我每次去和你的距离都会减一。无论我们会计人是走两步还是走三步走四步都会追上。如果是走技术的话,那么就是相当于转第二圈才能追上。并且这个不存在追不上的问题。我们经过认证证明是一定会追上的,不存在不上的条件。如果你的距离是奇数的话,那么就要转两圈才能追上,如果是偶数,则第一圈就追上了。
但是我们前面都是考虑的带环的,我们肯定也有不带环的呀。那么我们是不是当快指针或者快指针的下一步为NULL了?那么就代表他们走到结尾了,说明他们就不带环了。
那有没有存在当慢指针走到了相交节点?快指针还没有追上他呢。大家需要注意一下,这是不存在的。因为当慢指针走到相交节点就代表了他已经转了c一圈了。因为我们快指针比慢指针快。动漫直升都走了一圈了,快指针还没追上,那么就代表这个是不存在的。
我想当大家看到这里了,应该也大概了解了我们这个的解题思路是什么。就是创建两个指针从头开始往前走,一个走一步,一个走两步。当快指针与慢指针相等,那么就代表他们有还我们就返回ture否则就返回false
代码实现
其实这个就是很经典的想出来很难写出来很简单的问题了。我们上面也说过,我就是创建两个新节点,从头开始走,如果相遇了,那就返回ture反之亦然。
bool hasCycle(struct ListNode *head) {
struct ListNode* man=*head;
struct ListNode* kuai=*head;
while(kuai&&kuai->next)
{
man=man->next;
kuai=kuai->next->next;
if(man=kuai)
return ture;
}
return false;
}这写出来是很简单的。主要是大家能知道这个方法就好很多了。大家知道这个思想,但是如果我们在力扣上回答这个问题的话,需要变一下。但是我们思想是正确的。毕竟我用他们自己的这个题目的解题都会有报错。不知道为什么。
返回节点
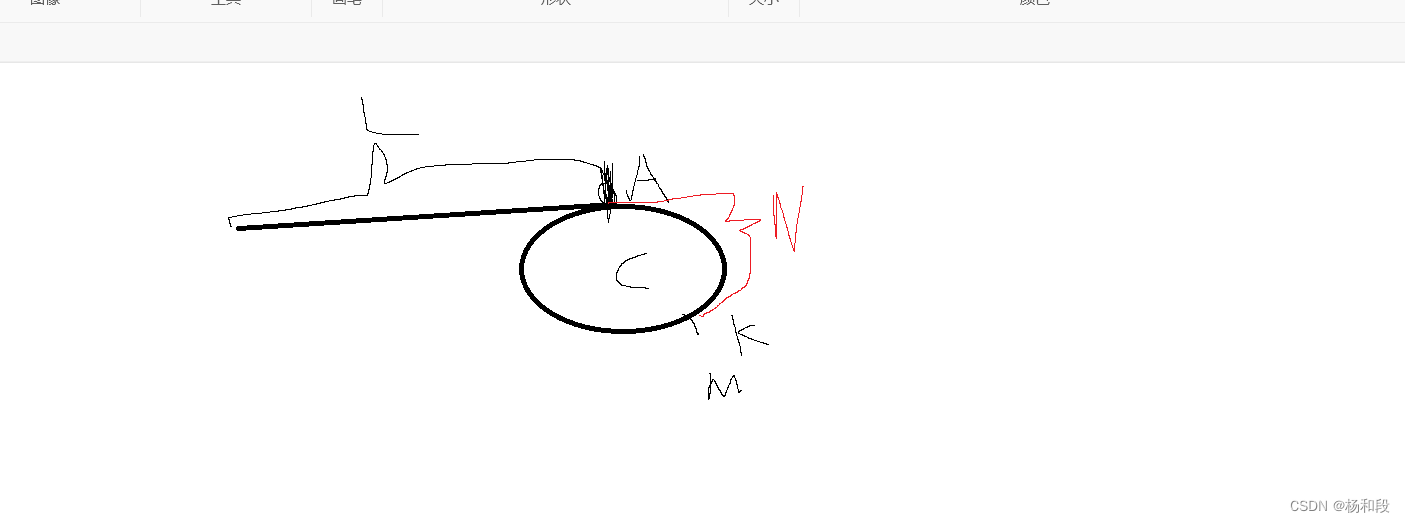
我们要返回节点的话,就是相当于我们要返回那个黑色的柱子A。我们在前面也说过了,h和相遇就代表有环,所以我们需要判断是否有a的话。我们有两种方法。但都会用到我们前面写的判断是否有环。因为我们要借用他们快慢相遇的那个节点。我们的第一种方法就是在快慢指针相遇的地方再创建一个节点。并且在l的开头创建一个节点,他们同时向是下走。当他们相遇,那么就返回这个节点,就说明这是我们的黑色柱子a了。大家会想想啊,这是为什么呀?为什么他们这就相遇了就返回这个节点了?大家可以看我接下来写一个公式,思考一下是不是这样的?

其中Y代表的是快指针是慢直针的几倍,然后右边代表的快指针走的步数。左指针是慢指针走的步数。 我们以快指针针是慢指针的二倍来计算。
其中x为快指针在c里面走了多少圈。这样看起来是不是减少出来?L就等于快慢指的相遇后面的节点嘛。 大家应该就了解很多了,那我们接下来就实现代码如何?
代码实现1
struct ListNode* meet=kuai;
while(meet!=head)
{
meet=meet->next;
head=head->next;
}
return meet大家看看这个代码是很简单的吧。那只需要创建一个新节点,就是在快慢指针的节点,然后一直循环。那么他们就一定会相遇,然后就返回这个节点就可以了。关于这个代码实现,大家最主要是理解它上面的公式是如何的。
代码实现2
我们在前面说过,这是我们返回去的第一种方法,我们还有个第二种方法。其实整体上是差不太多的。我们在他们快慢指针相遇点后创建一个新节点。然后再将快慢指针后的原节点给置为空。那么我们创建的新节点,它就是剩下链表的头节点了。加上我们原本的那个链表现在就是两个单链表了。然后就演变成了我们的另外一个问题,两个链表相交的问题。
那么接下来我们就直接写出链表相交的问题。然后大家就可以知道了。
我们看一下这个图。那两个单列表如果想要有交点的话,他们的尾巴是不是相同的呀?因为是单链表嘛。我们无法向前走,但我们只能从前往后走。那么我们就都往后走,一直走到尾,今天之后我们判断是否相同,如果相同,那么就代表他们肯定会有交点,如果不同,我们就返回null。
但大家需要注意的是我们判断的并不是他们两个的值是不相同,而是判断的地址是不相同。因为如果我们判断值的话,我们很有可能尾部的值是相同的,但地址不相同。那么这是不是就是一个问题了?所以我们判断他们尾节点是否相同的话,我们需要判断的是地址。
我们判断了他们有交点后。我看图片也可以看出来,有的列表长,有的列表短,我们这个也是需要单独判断的呀。那么我们怎么处理这件事情呢?我们从这些链表的头一起往后走的话,很有可能会错过这个交点。但是如果我们长的和短的从相同的位置开始出发的话,那么是否就会相遇了?因为我们知道当我们链表的长度相同的话,并且他们有焦点,那么焦点的位置相同,甚至说明他们前面的不是交点的部分也是相同的。那么我们现在就是需要过滤掉长的多的那一部分。所以我们是不是比较长链表与短链表,然后提前走掉他们相差的那部分,然后再一起往后走,判断他们相交的节点了。
并且我们也知道我们前面要计算尾节点,那我们可以在尾节点的同时计算出它们的个数,这样是不是只有就方便了许多。
void xxxx(struct list* a, struct list* b)
{
struct list *cur1 = a;
struct list *cur2 = b;//两个新节点
int y = 0;
int h = 0;//记录数字
while (cur1->next)
{
cur1 = cur1->next;
y++;
}
while (cur2->next)
{
cur2 = cur2->next;
h++;
}//走到尾节点,并且记录数
if (cur1 != cur2)
return NULL;//尾节点是否相同
int gap = abs(y - h);
struct list* max = cur1; struct list*min = cur2;
if (y < h)
{
int max = cur2; int min = cur1;
}//确立谁是快指针。假设法
while (gap--)
{
max = max->next;
}//快指针先走几步
while (max!=min)
{
max = max->next;
min = min->next;
}//一起走,然后返回节点
return max;
}上面的代码就是第二种方法的实现方法的,大家只需要在后面传入参数的时候将节点重新创建之后然后传头节点和这个节点就可以了。
总结
大家最主要的是了解这个代码的逻辑。这些代码实际上是运行起来其实没有太大的作用,最主要的是大家的逻辑能力能够得到有所锻炼,这相当于我们平常学习的有教学意义。实践的话可能没有多大作用。然后这上面就是我想与大家分享的知识了,然后肯定还有一些方法,但我不是很清楚,希望大家能在评论区里面留言。