LeetCode —— 只出现一次的数字

只出现一次的数字 I

本题依靠异或运算符的特性，两个相同数据异或等于0，数字与0异或为本身即可解答。代码如下:

cpp 复制代码

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ret = 0;
        for (auto e : nums)
        {
            ret ^= e;
        }
        return ret;
    }
};

只出现一次的数字 II

官方使用位运算题解代码如下：

cpp 复制代码

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ans = 0;
        for (int i = 0; i < 32; ++i) {
            int total = 0;
            for (int num: nums) {
                total += ((num >> i) & 1);
            }
            if (total % 3) {
                ans |= (1 << i);
            }
        }
        return ans;
    }
};

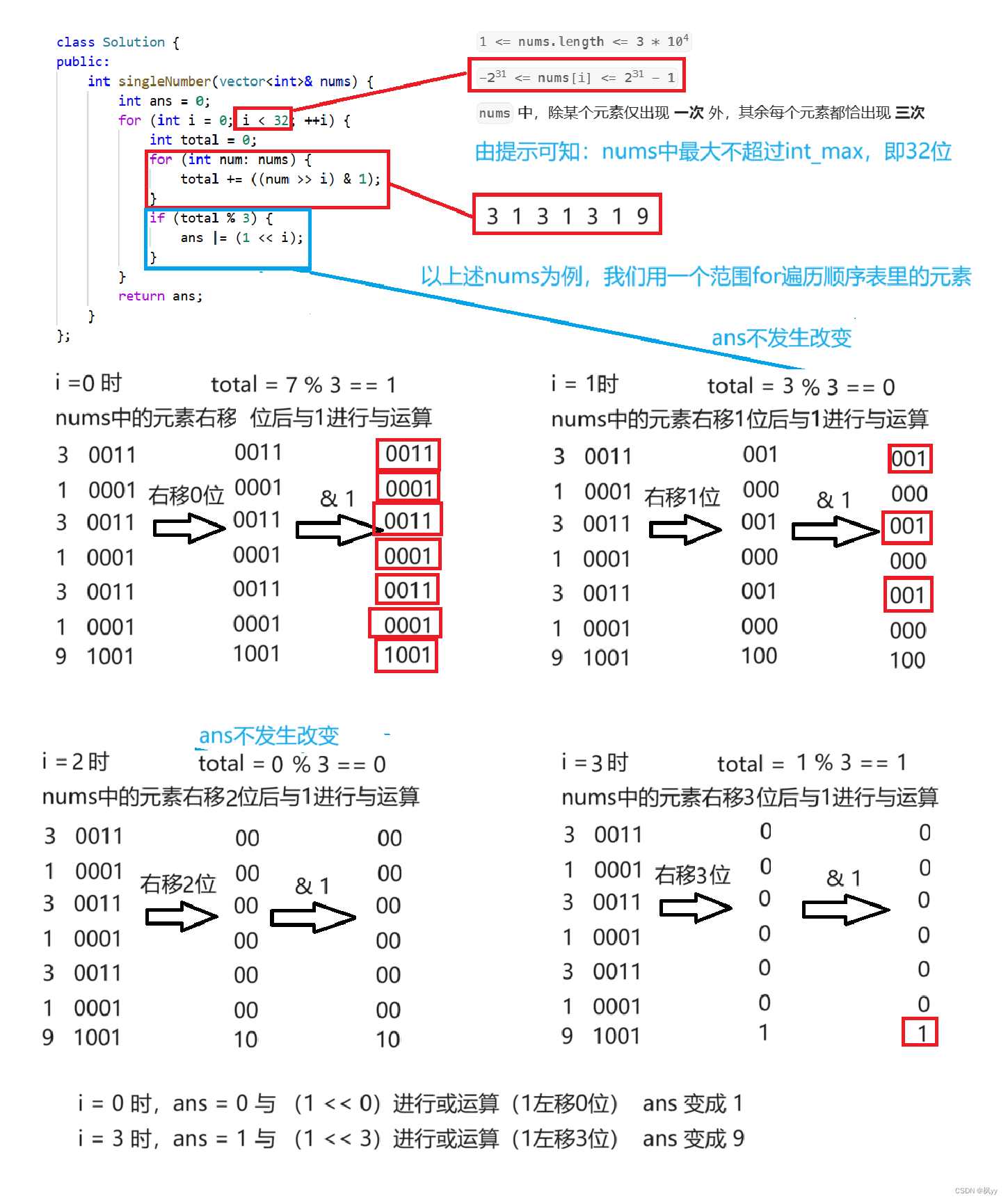
为什么可以这样实现呢？博主也是想了好久，现在解释原理：

若顺序表中的元素个数为奇数，那么一定有 2n 组出现 3 次的数和1个只出现一次的数组成，右移n位，由于出现 3 次的数是偶数个，那么与1进行与运算并相加后，必定为3的倍数 ，如果模3不等于0，只有一种可能：只出现一次的数为1使total不能被整除，说明只出现一次的数第 i 位为1，反之为0。

若顺序表中的元素个数为偶数，那么一定有2n + 1组出现三次的数和1个只出现一次的数组成，右移n位，由于出现 3 次的数是奇数个，那么与1进行与运算并相加后，必定为3的倍数 ，如果模 3 不等于 0 ，只有一种可能：只出现一次的数为1使total不能被整除，说明只出现一次的数第 i 位为1，反之为0。

只出现一次的数字 III

本人选择了一个较为好理解的答案，题解大神（灵茶山艾府）使用位运算题解代码如下：

cpp 复制代码

class Solution {
public:
    vector<int> singleNumber(vector<int>& nums) {
        // 负数在计算机是补码的形式存在
        // 无符号取负数就是取反加一
        unsigned int x = 0;
        for (auto e : nums)
        {
            x ^= e;
        }
        int lowbit = x & -x;
        // 此方法可以算出最低比特位  
        vector<int> ans(2);
        for (auto f : nums)
        {
            ans[(f & lowbit) != 0] ^= f;
        }
        return ans;
    }
};

看完图之后是否理解得更加深刻了呢？个人觉得第二次遍历相当巧妙，下面看大佬给出的解释：

希望本篇文章对你有帮助，有问题请在评论区指正，感谢阅读。