目录
引入:
当说黄河五路和渤海三路交叉口的时候,这些路就类似于我们说的坐标系。而城市中的每一个地方就类似于坐标系中的点,被坐标系唯一标识。 那么问题来了,我想让你把黄河五路渤海三路交叉口这样用两个数字标注的位置信息,转换为只有一个数字标识的位置描述,你怎么办?------ 如果有一条铁路通过了城市,而城市中所有重要的建筑都在铁路边,那么就可以根据距离铁路的起点多远来定义每一个点的位置。那样是不是这个问题就解决了?比如黄河五路渤海三路交叉口距离铁路挺近的,在起点旁边。 其实,这就是一种降维了,把原来的需要两个维度标注的信息,现在用一条铁路就可以搞定。
当然,这样的定位不如用俩个维度来的准,有的地点离铁路远,但是远多少,在新的表示中就没有得到展示了。这说明数据降维不是无损的,会造成信息的部分丢失。
主成分分析方法是一种数据降维的方式,只要数据压缩,必定会损失一些信息,而PCA做的就是尽可能的去找到一些主要的关键特征去区分开数据,去除掉一些对区分数据不大的那些特征,这样,既可以做到降维,也可以尽可能多的保留原来数据的信息。
一、概念
PCA------主成分分析法
属于无监督 学习方法,这一方法利用正交变换(也就是对原坐标系做旋转变换 )把由线性相关变量表示的观测数据转换为少数几个由线性无关变量表示的数据,线性无关的变量称作主成分。
简单来讲就是通过坐标轴转换对数据进行降维操作。选择坐标轴的依据是尽可能保留原始数据。降维即把数据投影在这个坐标轴上或者几个坐标轴构成的'平面'上。
二、原理
把数据看成空间中的点,然后尝试去寻找几个方向(例如下图橙色的和下面的PC1PC2), 把这些点进行投影,投影之后让这些点离得尽可能的远 。 这样这几个方向就是主成分, 空间中的样本点就可以通过这几个新的方向进行描述了。 但是找的这几个方向也是有要求的,就是互不干扰,没有线性关系,就像x轴和y轴那样,这样才能更好的去描述这些数据。主成分之间没有冗余。

所以主成分的标准两个条件:
①互不相关。 ②用来描述数据的时候,方差尽可能大。
三、步骤
梳理一下这个过程,然后我们根据一个例子感受一下这个过程,遇到新的数据集X之后(N维),我们想降到K维,PCA是这样做的
- 首先,应该先把X每一维进行归一化,把均值变成0
- 然后,计算协方差矩阵C, 即𝐶=1𝑚𝑋𝑛𝑜𝑟𝑚𝑋𝑛𝑜𝑟𝑚𝑇
- 然后,计算C的特征值和特征向量,把特征值从大到小排列,对应的特征向量从上往下排列
- 然后,将协方差矩阵相似对角化
- 然后,去特征向量的前k个,得到K个基
- 最后,用这K个基与X相乘,得到降维后的K维矩阵Y
下面我们看一个例子,感受一下这个过程:
1、输入数据X: 2个特征,5个训练样本, 并去均值

2、计算协方差矩阵C ,即𝐶=1𝑚𝑋𝑛𝑜𝑟𝑚𝑋𝑛𝑜𝑟𝑚𝑇
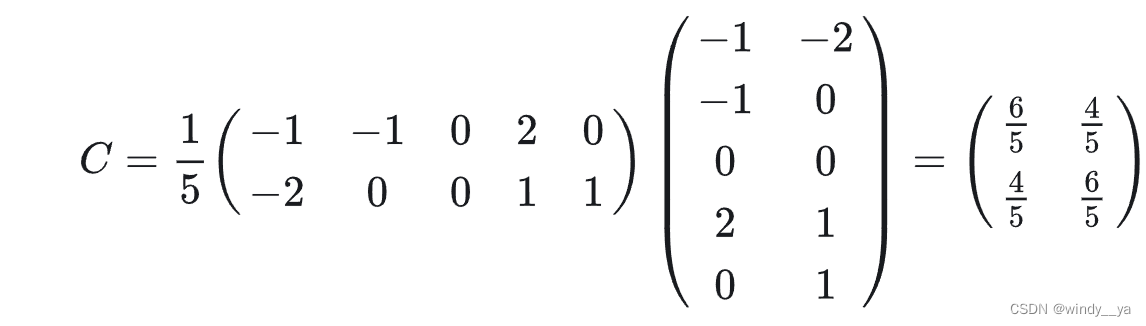
3、计算特征值和特征向量 特征值

4、相似对角化
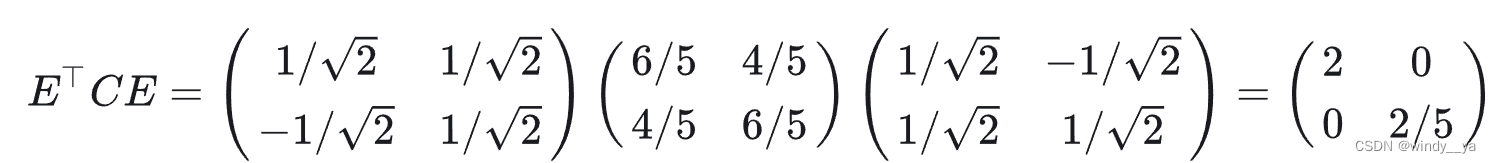
5、降到1维,那么就取𝑐1作为基,得最后结果

四、实战
原图如下,对其进行pca降维:

1、数据处理------转rgb为灰度图像
python
def loadImage(path):
img = Image.open(path)
# 将图像转换成灰度图
img = img.convert("L")
width = img.size[0]
height = img.size[1]
data = img.getdata()
# 对数据进行一个缩放,缩小100倍
data = np.array(data).reshape(height,width)/100
new_im = Image.fromarray(data*100)
new_im.show()
return data【输出】

2、手动实现pca降维
python
def pca(data,k):
#param data: 图像数据
#param k: 保留前k个主成分
n_samples,n_features = data.shape
# 求均值
mean = np.array([np.mean(data[:,i]) for i in range(n_features)])
# 去中心化
normal_data = data - mean
# 得到协方差矩阵
matrix_ = np.dot(np.transpose(normal_data),normal_data)
eig_val,eig_vec = np.linalg.eig(matrix_)
# print(matrix_.shape)
# print(eig_val)
# 第一种求前k个向量
# eig_pairs = [(np.abs(eig_val[i]),eig_vec[:,i]) for i in range(n_features)]
# eig_pairs.sort(reverse=True)
# feature = np.array([ele[1] for ele in eig_pairs[:k]])
# new_data = np.dot(normal_data,np.transpose(feature))
# 第二种求前k个向量
eigIndex = np.argsort(eig_val)
eigVecIndex = eigIndex[:-(k+1):-1]
feature = eig_vec[:,eigVecIndex]
new_data = np.dot(normal_data,feature)
# 将降维后的数据映射回原空间
rec_data = np.dot(new_data,np.transpose(feature))+ mean
# print(rec_data)
# 压缩后的数据也需要乘100还原成RGB值的范围
newImage = Image.fromarray(rec_data*100)
newImage.show()
return rec_data这里取的保留前十个主成分,得到

3、查看信息保留数量
python
def error(data,recdata):
sum1 = 0
sum2 = 0
# 计算两幅图像之间的差值矩阵
D_value = data - recdata
# 计算两幅图像之间的误差率,即信息丢失率
for i in range(data.shape[0]):
sum1 += np.dot(data[i],data[i])
sum2 += np.dot(D_value[i], D_value[i])
error = sum2/sum1
print(sum2, sum1, error)
python
23076.032446296413 2261348.8400000017 0.0102045434291758344、调用第三方库实现pca降维
python
import numpy as np
from sklearn.decomposition import PCA
from PIL import Image
def loadImage(path):...
def error(data, recdata):...
if __name__ == '__main__':
data = loadImage("timg.jpg")
pca = PCA(n_components=10).fit(data)
# 降维
x_new = pca.transform(data)
# 还原降维后的数据到原空间
recdata = pca.inverse_transform(x_new)
# 计算误差
error(data, recdata)
# 还原降维后的数据
newImg = Image.fromarray(recdata*100)
newImg.show()
# error(data, recdata)得到的值跟上面不调库的差不多:
python
23076.032452099163 2261348.8400000017 0.010204543431741892五、小结
PCA优势:
1、降低数据维度:可以将高维数据压缩到低维空间,减少数据的存储和计算成本。
2、去除噪声:通过降维可以去除一些噪声和冗余信息,提高数据的质量。
3、可视化数据:将高维数据降维后,可以更直观地观察和分析数据的分布和特征。
但是可能会导致一些重要信息的丢失。