写在前面
源码 。
前缀树,又叫做trie树,字典树,是一种多叉的树,一般用于单词前缀匹配的相关场景中,比如:
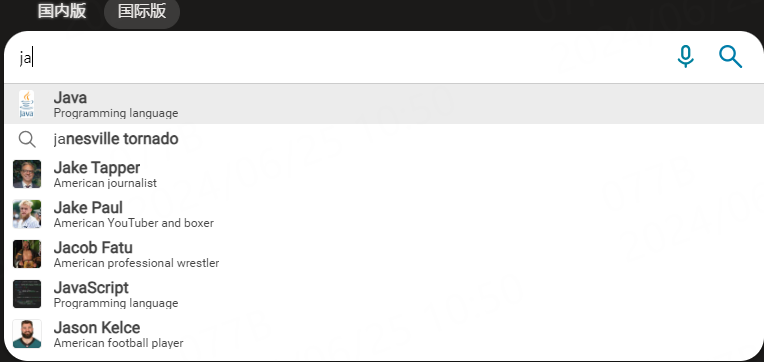
本文看下使用Java如何来实现这种数据结构。
1:基本介绍
思想:空间换时间,因为需要维护非常多的引用,所以比较占用空间,但能够快速定位所以时间较短
时间复杂度:log
特点:
根节点不包含字符
每一条路径所有节点的字符拼接在一起就对应一个字符串
拥有相同前缀的多个字符串共享相同前缀结构如下:
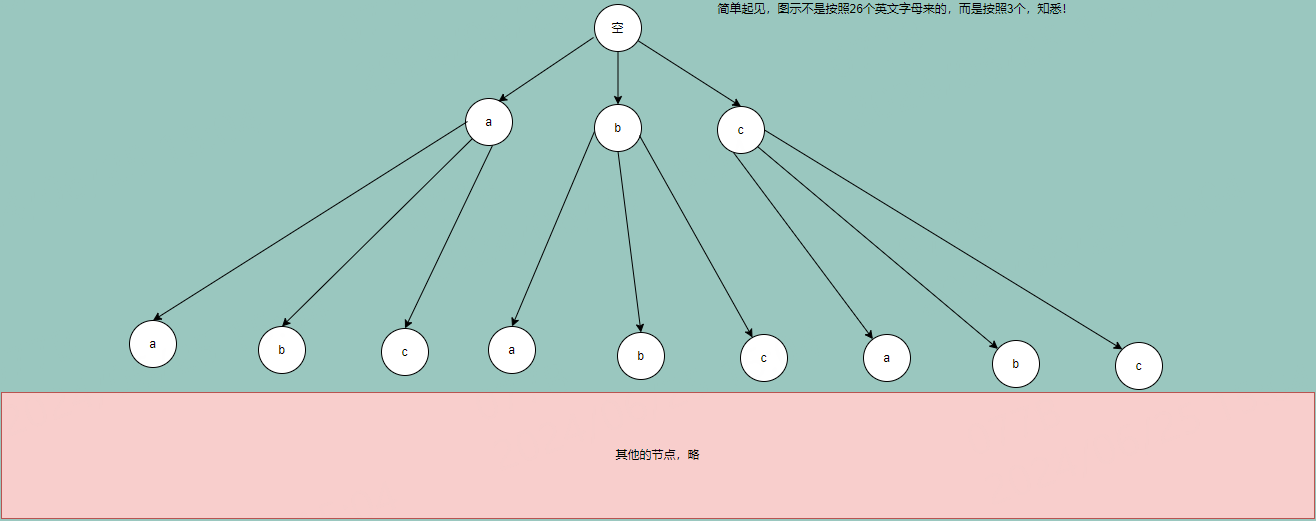
2:代码实现
定义节点类:
java
public class TreeNode {
//经过这个节点的字符串的个数(以这个节点为前缀的字符串的个数)
public int path;
//以这个节点结束的字符串的个数(有多少个字符串有这条路径的char组成)
public int end;
//对应着小写的a-z的26个字母(如果要更多可以使用hashmap<char,Node>
public TreeNode[] next;
// 是否为叶子节点
public boolean isLeaf = true;
// 是否为一个单词的结束字符
public boolean isWordEnd = false;
public TreeNode() {
path = 0;
end = 0;
next = new TreeNode[26];
}
@Override
public String toString() {
return "TreeNode{" +
"path=" + path +
", end=" + end +
", next=" + Arrays.toString(next) +
'}';
}
}定义前缀树类:
java
public class TrieTree {
public TreeNode root;
public TrieTree() {
root = new TreeNode();
}
/**
* 在前缀树中插入字符串
* 这种++的方法,导致,一个node,有多少个end,就有多少个相同的字符串
* 一个node,有多少个path,就有多少个字符串经过(root的path代表有多少个字符串)(字符串末尾的node的path也会++)
*
* @param string 被插入的字符串(以前插入过的也可以插入)
*/
public void insertString(String string) {
if (string == null || string.length() == 0) {
return;
}
int length = string.length();
TreeNode nowNode = root;
for (int i = 0; i < length; i++) {
char now = string.charAt(i);
int index = now - 'a';
//index为字符now所处的位置
if (nowNode.next[index] == null) {
nowNode.next[index] = new TreeNode();
}
nowNode.isLeaf = false;
// 先对当前node的path++,再转移到下一个node
nowNode.path++;
nowNode = nowNode.next[index];
}
// 处理 ab abc ,通过前缀a查询,也需要查询出ab的情况
nowNode.isWordEnd = true;
//在最后的node,path和end++
nowNode.path++;
nowNode.end++;
}
/**
* 返回这个前缀树总共插入了多少个字符串
*
* @return
*/
public int size() {
return root.path;
}
/**
* 前缀树查询总共插入这个字符串多少次,如果没插入过,则返回0
*
* @param string
* @return
*/
public int getStringNum(String string) {
if (string == null || string.length() == 0) {
return 0;
}
int length = string.length();
TreeNode nowNode = root;
for (int i = 0; i < length; i++) {
char now = string.charAt(i);
int index = now - 'a';
//如果没有这个节点,说明不存在,直接返回0
if (nowNode.next[index] == null) {
return 0;
}
nowNode = nowNode.next[index];
}
//此时nowNode已经处于最后一个节点
return nowNode.end;
}
/**
* 前缀树查询以这个字符串为前缀的字符串总共多少个(包括以他为结尾的)
*
* @param string 前缀
* @return
*/
public int getPrefixNum(String string) {
if (string == null || string.length() == 0) {
return 0;
}
int length = string.length();
TreeNode nowNode = root;
for (int i = 0; i < length; i++) {
char now = string.charAt(i);
int index = now - 'a';
//如果没有这个节点,说明前缀不存在,直接返回0
if (nowNode.next[index] == null) {
return 0;
}
nowNode = nowNode.next[index];
}
//此时nowNode已经处于前缀的最后一个节点
return nowNode.path;
}
// public List<String> findByPrefix(String prefix) {
public Set<String> findByPrefix(String prefix) {
// 注意:根节点不存储任何元素
TreeNode curNode = root;
int prefixLen = prefix.length();
// 1:找到prefix对应的TreeNode对象
for (int i = 0; i < prefixLen; i++) {
int idx = prefix.charAt(i) - 'a';
TreeNode[] dataArr = curNode.next;
if (dataArr[idx] == null) {
System.out.println("not find!");
return null;
}
// 非前缀的最后一个元素,遇到空,则说明要匹配的前缀不存在
/*if (dataArr[idx] != null) {
if (i > prefixLen - 1) {
return null;
} else {
curNode = dataArr[idx];
}
}*/
// 继续向下
curNode = dataArr[idx];
}
// 2:根据prefix对应的TreeNode对象,递归找到所有的可能字符串
TreeNode[] possibleTreeNodeArr = curNode.next;
// 3:递归找到所有的可能字符串
// List<String> possibleStrList = new ArrayList<>();
Set<String> possibleStrList = new HashSet<>();
/*for (int i = 0; i < possibleTreeNodeArr.length; i++) {
if (possibleTreeNodeArr[i] != null) possibleStrList.add(prefix + (char) (i + 'a'));
}
for (int i = 0; i < possibleTreeNodeArr.length; i++) {
queryAllPossibleStr(i, possibleTreeNodeArr, possibleStrList, prefix);
}*/
queryAllPossibleStr(0, curNode, possibleTreeNodeArr, possibleStrList, prefix);
return possibleStrList;
}
private void queryAllPossibleStr(int i, TreeNode curNode, TreeNode[] possibleTreeNodeArr, Set<String> possibleStrList, String prefix) {
if (i >= possibleTreeNodeArr.length || possibleTreeNodeArr == null) return;
String newPrefix = prefix + (char) (i + 'a');
// 元素为null,说明到达叶子节点
if ((possibleTreeNodeArr[i] == null && curNode.isLeaf) || curNode.isWordEnd) {
// if (possibleTreeNodeArr[i] == null && i == possibleTreeNodeArr.length - 1) {
// if (possibleTreeNodeArr[i] != null && possibleTreeNodeArr[i].isLeaf) {
possibleStrList.add(prefix);
// 下层
// queryAllPossibleStr(0, possibleTreeNodeArr[i], possibleTreeNodeArr[i].next, possibleStrList, newPrefix);
} /*else {
// 当前无元素,则向右继续找,有则向下和向右找
if (possibleTreeNodeArr[i] != null) {
// 下层
queryAllPossibleStr(0, possibleTreeNodeArr[i], possibleTreeNodeArr[i].next, possibleStrList, newPrefix);
}
}*/
// 当前无元素,则向右继续找,有则向下和向右找
if (possibleTreeNodeArr[i] != null) {
// 下层
queryAllPossibleStr(0, possibleTreeNodeArr[i], possibleTreeNodeArr[i].next, possibleStrList, newPrefix);
}
// 不管咋的,都得向右→
queryAllPossibleStr(i + 1, curNode, possibleTreeNodeArr, possibleStrList, prefix);
}
}重点关注两个方法,insertString插入方法,findByPrefix根据前缀获取匹配前缀的字符串列表方法。
测试代码:
java
public class Main {
public static void main(String[] args) {
TrieTree tree=new TrieTree();
tree.insertString("aba");
tree.insertString("abc");
tree.insertString("abcd");
tree.insertString("jack");
tree.insertString("amazing");
tree.insertString("express");
tree.insertString("engine");
tree.insertString("engines");
tree.insertString("equipment");
tree.insertString("j");
// tree.insertString("aa");
// tree.insertString("aa");
// tree.insertString("ab");
// tree.insertString("ba");
// tree.insertString("jack");
// tree.insertString("jaabcdef");
//System.out.println(tree.root);
//System.out.println(tree.size());
//System.out.println(tree.getStringNum("aa"));
//System.out.println(tree.getStringNum("ab"));
//System.out.println(tree.getStringNum("ac"));
System.out.println(tree.getPrefixNum("a"));
System.out.println(tree.getPrefixNum("b"));
System.out.println(tree.getPrefixNum("c"));
System.out.println(tree.findByPrefix("a"));
System.out.println(tree.findByPrefix("en"));
}
}运行:
[aba, amazing, abc, abcd]
[engine, engines]
[INFO] ------------------------------------------------------------------------
[INFO] BUILD SUCCESS
[INFO] ------------------------------------------------------------------------3:有啥用
比如你要开发一个自动提示补全的idea插件,就像这样:
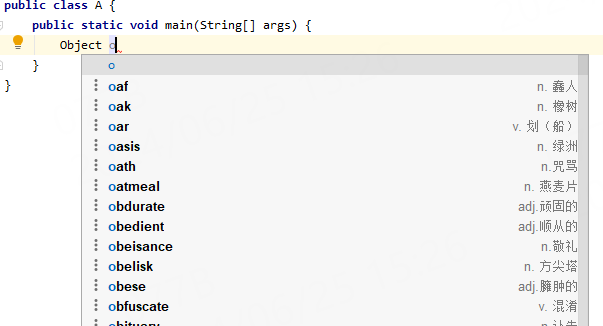
或者有其他的功能需要用到类似的功能,都可以考虑使用前缀树。
写在后面
不管是什么技术,只有用到了实际的功能中才算是真正的有用,因此在实际工作中我们要往如何落地应用的方向多考虑。