目录
[1. 哈希表核心概念](#1. 哈希表核心概念)
[2. 哈希表的实现](#2. 哈希表的实现)
[3. 哈希表的拓展知识](#3. 哈希表的拓展知识)
[1. 排序算法:从无序到有序](#1. 排序算法:从无序到有序)
[2. 查找算法:从有序 / 无序中定位目标](#2. 查找算法:从有序 / 无序中定位目标)
[3. 排序与查找算法的拓展](#3. 排序与查找算法的拓展)
一、哈希表:高效存取数据
1. 哈希表核心概念
哈希表(Hash Table)是一种通过哈希算法实现键值映射的数据结构,其核心目标是将数据的存取时间复杂度尽可能降低至 O (1)。
- 哈希算法:将数据通过特定函数映射为一个键值(索引),数据的存储和查找均基于该键值进行,大幅减少了比较操作。
- 哈希碰撞:当多个数据通过哈希算法映射到同一键值时,称为哈希碰撞。这是哈希表设计中必须解决的核心问题。
2. 哈希表的实现
文档中以存储 0-100 之间的数据为例,选择 "数据的个位作为键值" 作为哈希算法,通过链表解决碰撞(链地址法),实现了哈希表的基本操作:
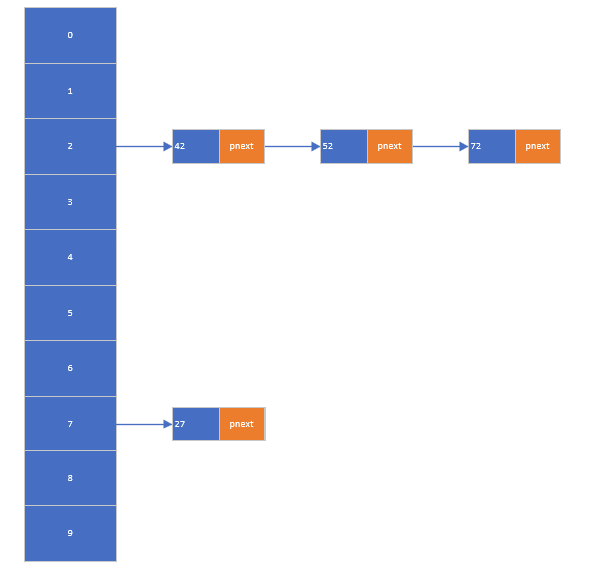
(1)插入操作
通过哈希算法计算键值后,将数据插入对应链表的合适位置(保持链表有序):
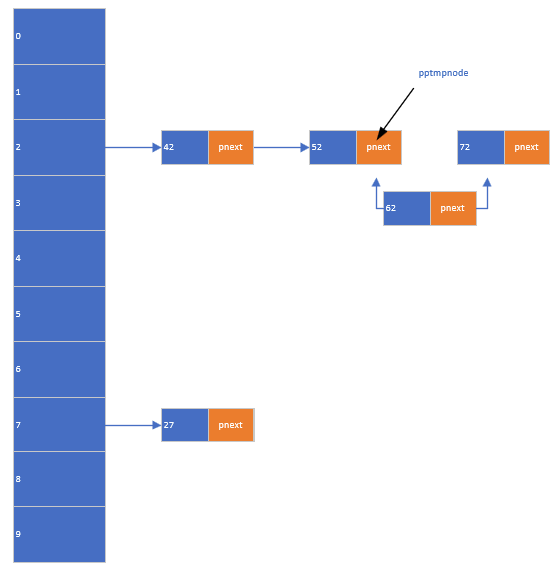
int insert_hashtable(int tmpdata) {
int key = 0;
linknode **pptmpnode = NULL;
linknode *pnewnode = NULL;
key = tmpdata % INDEX; // 计算键值(个位)
for (pptmpnode = &phashtable[key]; *pptmpnode != NULL && (*pptmpnode)->data < tmpdata; pptmpnode = &(*pptmpnode)->pnext);
// 申请节点并插入
pnewnode = malloc(sizeof(linknode));
if (NULL == pnewnode) {
perror("fail to malloc");
return -1;
}
pnewnode->data = tmpdata;
pnewnode->pnext = *pptmpnode;
*pptmpnode = pnewnode;
return 0;
}(2)遍历操作
按键值顺序遍历所有链表,输出哈希表中的全部数据:
int show_hashtable(void) {
int i = 0;
linknode *ptmpnode = NULL;
for (i = 0; i < INDEX; i++) {
printf("%d:", i);
ptmpnode = phashtable[i];
while (ptmpnode != NULL) {
printf("%2d ", ptmpnode->data);
ptmpnode = ptmpnode->pnext;
}
printf("\n");
}
return 0;
}(3)查找操作
通过键值定位到对应链表,再遍历链表查找目标数据:
linknode *find_hashtable(int tmpdata) {
int key = 0;
linknode *ptmpnode = NULL;
key = tmpdata % INDEX;
ptmpnode = phashtable[key];
while (ptmpnode != NULL && ptmpnode->data <= tmpdata) {
if (ptmpnode->data == tmpdata) {
return ptmpnode;
}
ptmpnode = ptmpnode->pnext;
}
return NULL;
}(4)销毁操作
释放所有链表节点及哈希表空间:
int destroy_hashtable(void) {
int i = 0;
linknode *ptmpnode = NULL;
linknode *pfreenode = NULL;
for(i = 0; i < INDEX; i++) {
ptmpnode = phashtable[i];
pfreenode = phashtable[i];
while (ptmpnode != NULL) {
ptmpnode = ptmpnode->pnext;
free(pfreenode);
pfreenode = ptmpnode;
}
phashtable[i] = NULL;
}
return 0;
}3. 哈希表的拓展知识
(1)哈希函数设计原则
- 均匀性:尽可能将数据均匀分布到哈希表的各个位置,减少碰撞概率;
- 高效性:计算过程简单,避免复杂运算影响性能;
- 稳定性:相同数据应映射到相同键值。
常见哈希函数:除留余数法(文档所用)、平方取中法、折叠法、数字分析法等。
(2)哈希碰撞解决方法
- 链地址法(文档所用):将碰撞的数据存储在同一键值对应的链表中,结构简单且处理灵活;
- 开放定址法:当发生碰撞时,通过线性探测、二次探测等方式寻找下一个空闲位置;
- 再哈希法:使用多个哈希函数,若第一个函数碰撞则使用第二个,直到找到空闲位置;
- 建立公共溢出区:将所有碰撞的数据统一存放到溢出表中。
(3)哈希表的应用场景
- 数据库索引:通过哈希索引快速定位记录;
- 缓存系统:如 Redis 中哈希表用于存储键值对;
- 查找表:如字典、集合等数据结构的底层实现。
二、排序与查找算法:数据处理的核心工具
1. 排序算法:从无序到有序
排序算法用于将一组数据按照特定顺序(升序 / 降序)排列,文档中介绍了 5 种经典排序算法,以下是整理与拓展:
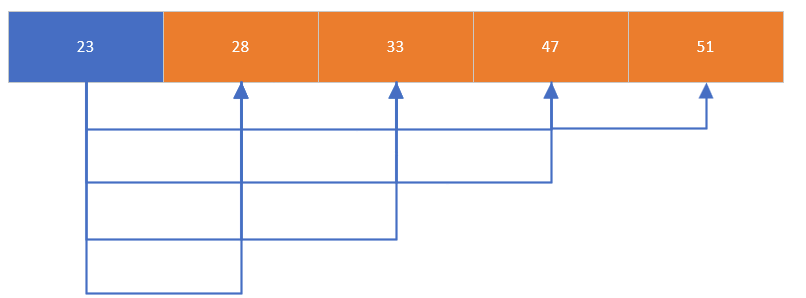
(1)冒泡排序
-
原理:通过相邻元素的比较和交换,使大元素 "冒泡" 到数组末尾,循环找出 n-1 个最大值;
-
时间复杂度:O(n²);
-
稳定性:稳定(相等元素不交换位置);
-
代码实现:
int bubble_sort(int *parray, int len) {
int i = 0;
int j = 0;
int tmp = 0;
for (j = 0; j < len-1; j++) {
for (i = 0; i < len-1-j; i++) {
if (parray[i] > parray[i+1]) {
tmp = parray[i];
parray[i] = parray[i+1];
parray[i+1] = tmp;
}
}
}
return 0;
}
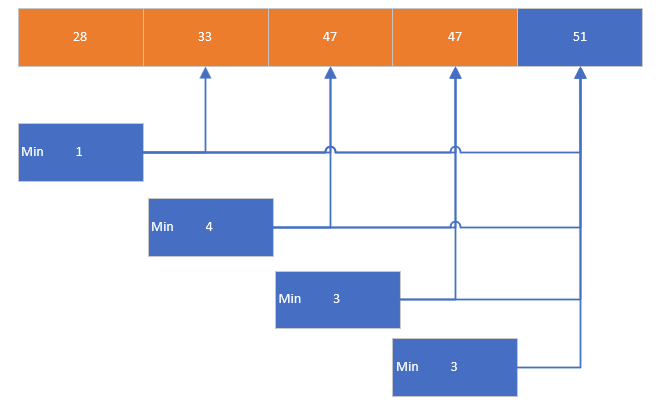
(2)选择排序
-
原理:从待排序区间中找到最小值,与区间首个元素交换,循环找出 n-1 个最小值;
-
时间复杂度:O(n²);
-
稳定性:不稳定(可能交换相等元素的相对位置);
-
代码实现:
int select_sort(int *parray, int len) {
int i = 0;
int j = 0;
int tmp = 0;
int min = 0;
for (j = 0; j < len-1; j++) {
min = j;
for (i = j+1; i < len; i++) {
if (parray[i] < parray[min]) {
min = i;
}
}
if (min != j) {
tmp = parray[min];
parray[min] = parray[j];
parray[j] = tmp;
}
}
return 0;
}
(3)插入排序
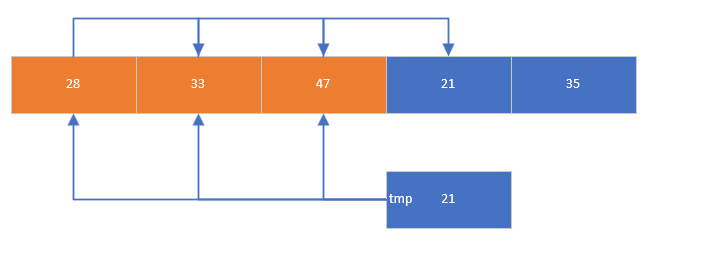
-
原理:将元素逐个插入到已排序区间的合适位置,类似整理扑克牌;
-
时间复杂度:O (n²)(有序数组可优化至 O (n));
-
稳定性:稳定;
-
代码实现:
int insert_sort(int *parray, int len) {
int tmp = 0;
int i = 0;
int j = 0;
for (j = 1; j < len; j++) {
tmp = parray[j];
for (i = j; i > 0 && tmp < parray[i-1]; i--) {
parray[i] = parray[i-1];
}
parray[i] = tmp;
}
return 0;
}
(4)希尔排序
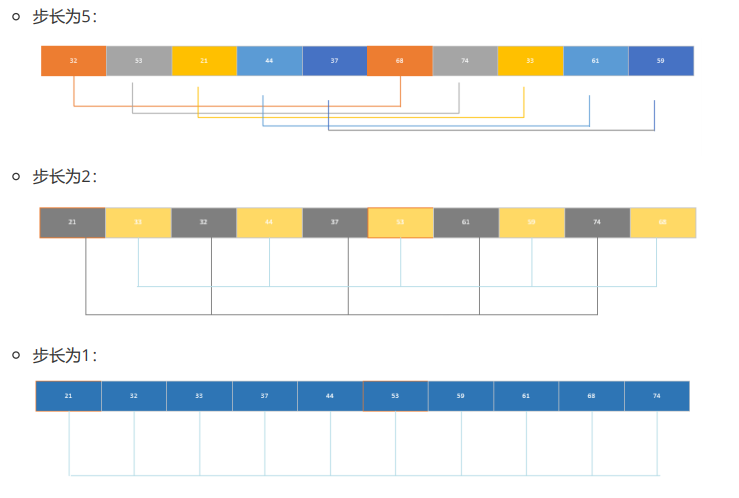
-
原理:通过 "步长" 将数组拆分为多个子数组,分别进行插入排序,逐步减小步长至 1,最终完成整体排序;
-
时间复杂度 :
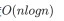 与步长选择相关,通常在 O (n¹.³)~O (n²) 之间;
与步长选择相关,通常在 O (n¹.³)~O (n²) 之间; -
稳定性:不稳定;
-
代码实现:
int shell_sort(int *parray, int len) {
int step = 0;
int j = 0;
int i = 0;
int tmp = 0;
for (step = len/2; step > 0; step /= 2) {
for (j = step; j < len; j++) {
tmp = parray[j];
for (i = j; i >= step && tmp < parray[i-step]; i -= step) {
parray[i] = parray[i-step];
}
parray[i] = tmp;
}
}
return 0;
}
(5)快速排序
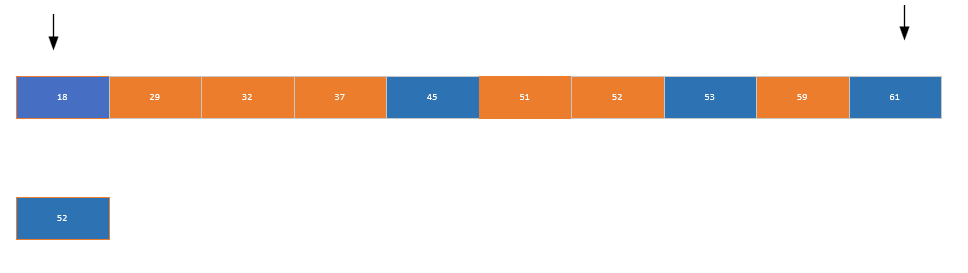
-
原理:选择一个 "枢轴" 元素,将数组分为 "小于枢轴" 和 "大于枢轴" 两部分,递归排序子数组;
-
时间复杂度:平均 O (nlogn),最坏 O (n²)(可通过优化枢轴选择避免);
-
稳定性:不稳定;
-
代码实现:
int quick_sort(int *parray, int low, int high) {
int key = 0;
int j = 0;
int i = 0;
key = parray[low];
j = high;
i = low;
while (i < j) {
while (i < j && parray[j] >= key) {
j--;
}
if (i < j) {
parray[i] = parray[j];
}
while (i < j && parray[i] <= key) {
i++;
}
if (i < j) {
parray[j] = parray[i];
}
}
parray[i] = key;
if (i-1 > low) {
quick_sort(parray, low, i-1);
}
if (i+1 < high) {
quick_sort(parray, i+1, high);
}
return 0;
}
2. 查找算法:从有序 / 无序中定位目标
查找算法用于从数据集中定位目标元素,文档介绍了两种经典算法:
(1)顺序查找
- 原理:从数据开头逐个遍历,直到找到目标或遍历结束;
- 时间复杂度:O(n);
- 适用场景:无序数据或小规模数据。
(2)折半查找(二分查找)
-
原理:仅适用于有序数组,通过比较中间元素与目标,缩小查找区间(左半或右半);
-
时间复杂度:O(logn);
-
代码实现:
int mid_search(int *parray, int low, int high, int tmpdata) {
int mid = 0;
if (low > high) {
return -1;
}
mid = (low + high) / 2;
if (tmpdata == parray[mid]) {
return mid;
} else if (tmpdata > parray[mid]) {
return mid_search(parray, mid+1, high, tmpdata);
} else if (tmpdata < parray[mid]) {
return mid_search(parray, low, mid-1, tmpdata);
}
}
3. 排序与查找算法的拓展
(1)排序算法对比与选择
| 算法 | 平均时间复杂度 | 稳定性 | 适用场景 |
|---|---|---|---|
| 冒泡排序 | O(n²) | 稳定 | 小规模数据 |
| 选择排序 | O(n²) | 不稳定 | 对稳定性无要求的小规模数据 |
| 插入排序 | O(n²) | 稳定 | 基本有序或小规模数据 |
| 希尔排序 | O(n¹.³) | 不稳定 | 中大规模数据 |
| 快速排序 | O(nlogn) | 不稳定 | 大规模数据(平均性能最优) |
(2)其他常用查找算法
- 插值查找:基于二分查找改进,根据目标与首尾元素的比例动态计算中间位置,适用于均匀分布数据;
- 斐波那契查找:利用斐波那契数列分割区间,减少比较次数,适用于黄金比例分布数据;
- 哈希查找:结合哈希表,平均时间复杂度 O (1),但需处理碰撞。
总结
哈希表通过键值映射实现高效存取,是解决快速查找问题的核心结构;排序算法则通过不同策略将数据有序化,为高效查找(如二分查找)奠定基础。理解这些数据结构与算法的原理、实现及适用场景,能帮助我们在实际开发中选择最优方案,提升程序性能。