Yi K, Zhang Q, Fan W, et al. FourierGNN: Rethinking multivariate time series forecasting from a pure graph perspective[J]. Advances in Neural Information Processing Systems, 2024, 36.
本次介绍的文章来自NeurIPS 2023,关于多变量时间序列的预测
摘要
痛点问题:当前最先进的基于图神经网络(GNN)的预测方法通常需要图网络(如GCN)和时间网络(如LSTM)来分别捕获序列间(空间)动态和序列内(时间)依赖关系。然而,两种网络的不确定兼容性给手工制作的模型设计带来了额外的负担。此外,分离的时空建模自然违背了现实世界中统一的时空相互依赖关系,这在很大程度上影响了预测效果。
解决方案:从纯图角度重新思考MTS预测
主要内容:首先定义了一种新的数据结构,hypervariate graph ,它将每个序列值(无论变量或时间戳)视为一个图节点,并将滑动窗口表示为时空全连接图 。该视角统一考虑时空动态,将经典的MTS预测重新表述为对超变量图的预测。然后,我们提出了一种新的傅立叶图神经网络(FourierGNN)架构 ,通过堆叠我们提出的**傅立叶图算子(FGO)**在傅立叶空间中执行矩阵乘法。FourierGNN具有较强的表达能力和较低的复杂度,能够有效地完成预测。此外,我们的理论分析揭示了FGO在时域上与图卷积的等价性,进一步验证了FourierGNN的有效性。在七个数据集上进行的大量实验表明,与最先进的方法相比,我们的性能更优,效率更高,参数更少。
一、介绍
多变量时间序列的预测:交通系统中的交通流量预测,天气预报中的温度估计,能源市场中的电力消耗规划等
传统方法:RNN、CNN、Informer ,但没有捕获序列的空间关系
基于GNN预测的方法(如STGCN , TAMPS2GCNets)严重依赖于预定义的图结构来指定;
后来的高级方法(如StemGNN[10]、MTGNN[13]、AGCRN[2])可以在没有预定义先验的情况下自动学习序列间相关性并相应地建模空间动力学,但几乎所有方法都是通过堆叠图网络(如GCN和GAT)来捕获空间动力学,通过堆叠图网络(如LSTM和GRU)来捕获时间依赖性。然而,图网络与时态网络的不确定兼容性给手工模型设计带来了额外的负担,影响了预测效果。
研究问题:即使没有时间网络,纯图网络也能捕获空间动态和时间依赖性吗?
提出的解决方案:提出了一种新的方法,称为傅里叶图神经网络(FourierGNN)。考虑将时域信息转移到频域,在傅里叶空间内利用纯图方法捕获时间序列的时空关系。
创新点
(1)时间上和空间上分别建图,破坏了时空整体性 -> 因此提出纯图网络捕获空间动态和时间依赖性
(2)纯图网络的特征挖掘开销大,计算成本高 -> 将时域上的计算转移到频域,利用傅里叶图算子(FGO)进行特征挖掘
(3)利用数学知识证明了在傅里叶空间中进行矩阵乘法等价于时间域中的图卷积
(4)实验十分丰富,数据集涵盖范围广,实验对比丰富,消融实验、可解释性实验都很丰富
二、相关工作
略
三、问题定义
给定一个多变量时间序列输入: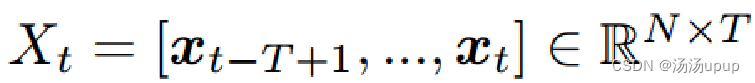
最终的预测任务是:

其中F是预测函数,Y是最终的预测值
四、方法
模型整体结构:
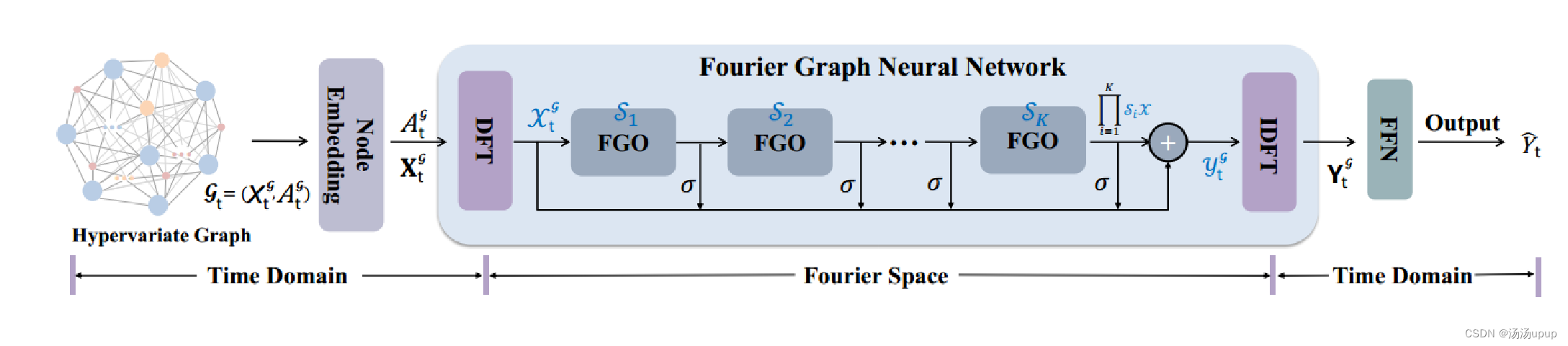
过程:(1)建图:构建全连通变量图 (2)节点嵌入:使用嵌入矩阵为每个节点嵌入d维向量 (3)离散傅里叶变换:将时域转到频域 (4)在傅里叶空间进行一系列递归乘法 (5)进行逆傅里叶变换:转回时域 (6)使用两层前馈网络FNN投影
1、建图
构建一个全连通变量图

这里的节点代表每个序列的采样点,边是全连通的,对于一个长度为T有N元的时间序列来说,超图具有NT个节点。
2、节点嵌入和离散傅里叶变换
使用嵌入矩阵为每个节点分配一个d维向量,即
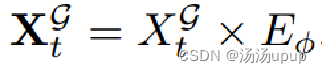
然后进行离散傅里叶变换:离散傅里叶变换(Discrete Fourier Transform)是信号分析中的一种基本方法,将离散时序信号从时间域变换到频率域,是傅里叶变换在时域和频域都呈离散的形式
3、 傅里叶图算子(Fourier Graph Operator)
给定一个图G=(X,A) 节点特征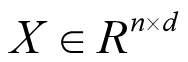 邻接矩阵
邻接矩阵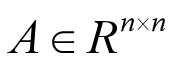 引入一个权重矩阵
引入一个权重矩阵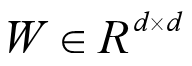
有一个特定的Green Kernel: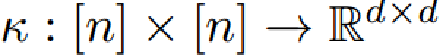 满足关系
满足关系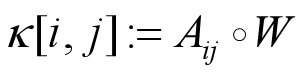 且
且 (平移不变性)
(平移不变性)
定义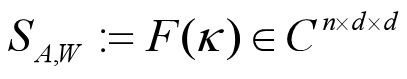 为傅里叶图算子(FGO) 其中F为离散傅里叶变换 将节点特征的傅里叶变换与FGO的乘积表示为:
为傅里叶图算子(FGO) 其中F为离散傅里叶变换 将节点特征的傅里叶变换与FGO的乘积表示为:
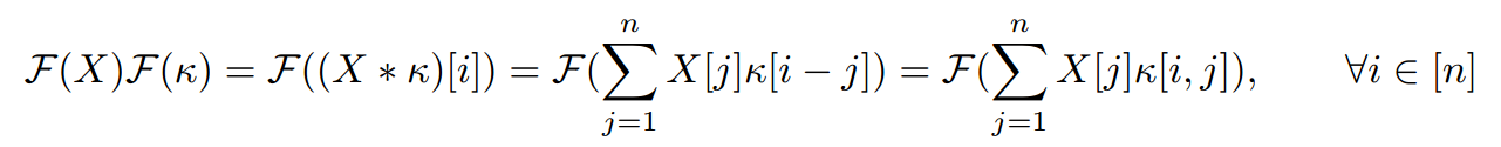
上述式子的原理来源于卷积定理:它表示两个信号卷积的傅里叶变换等于它们的傅里叶变换在频域中的点积
最终得到频域的卷积公式:

4、FourierGNN中的FGO应用
定义k层傅立叶图神经网络为:

其中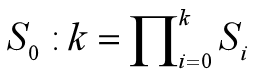 表示第k层的FGO,σ是激活函数,bk是偏置
表示第k层的FGO,σ是激活函数,bk是偏置
递归乘法在傅里叶空间中等效于时域中的多阶卷积:
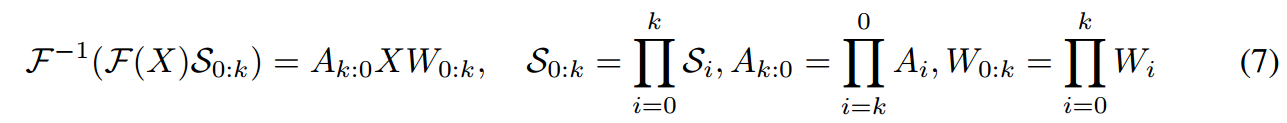
这种方法确保了FourierGNN在傅里叶空间中的操作与传统的时域卷积在理论上的一致性。
5、时间复杂度分析
假设有 𝑛个节点和 𝑑维特征,FourierGNN的时间复杂度可以分为以下几个部分:
(1)离散傅里叶变换(DFT)
DFT用于将节点特征从时域转换到傅里叶空间。对 𝑛个节点进行 DFT 的时间复杂度为 由于有d维特征,因此总的时间复杂度为:
(2)傅里叶空间中的矩阵乘法
在傅里叶空间中进行的矩阵乘法涉及节点特征矩阵 𝑋和傅里叶图算子 𝑆的乘法 假设 𝑋的尺寸为 𝑛×𝑑,𝑆的尺寸为 𝑑×𝑑这种矩阵乘法的时间复杂度为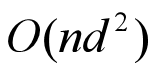
(3)逆离散傅里叶变换(IDFT)
IDFT用于将傅里叶空间中的结果转换回时域。IDFT的时间复杂度与DFT相同,为 由于有d维特征,因此总的时间复杂度为:
因此FGO的总时间复杂度为:
而传统卷积的时间复杂度为: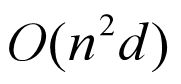
因此,FGO的复杂度明显低于传统的图卷积操作,尤其是在处理大规模图数据时,优势更加显著
五、结果
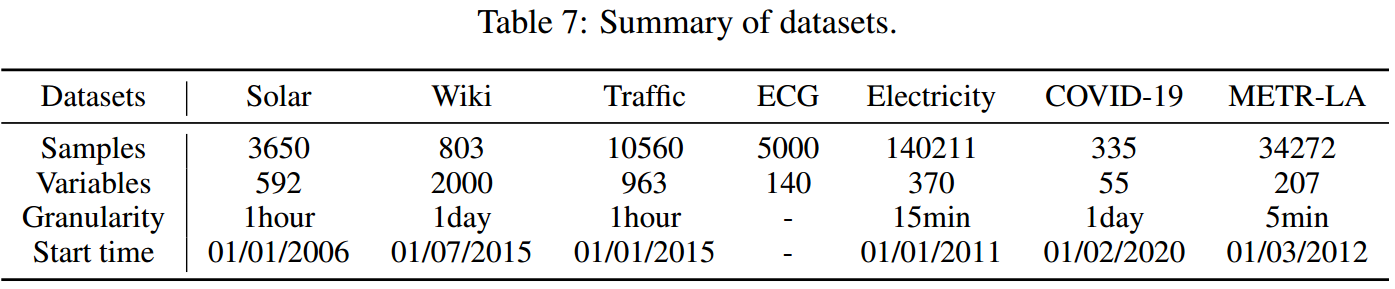
1、数据集
Solar: 这个数据集是关于国家可再生能源实验室收集的太阳能。我们选择佛罗里达州的发电厂数据点作为数据集,该数据集包含593个点。数据采集时间为2006年1月1日至2016年12月31日,每隔1小时采样一次。
Wiki: 该数据集包含了不同维基百科文章的每日浏览量,收集时间为2015/7/1至2016/12/31。它由大约145k个时间序列组成,我们随机从中选择2k个作为我们的实验数据集。
交通: 该数据集包含963个旧金山高速公路车道的每小时交通数据。流量数据从2015/01/01开始采集,每隔1小时采样一次。
ECG: 该数据集是关于UCR时间序列分类档案中的心电图(ECG)。它包含140个节点,每个节点的长度为5000。
electry: 该数据集包含370个客户的用电量,从2011年1月1日开始收集。每隔15分钟采样一次。
COVID-19: 该数据集是关于2020年2月1日至2020年12月31日美国加利福尼亚州COVID-19住院情况的数据集,由约翰霍普金斯大学提供,采样间隔为每一天。
**METR-LA:**该数据集包含2012年3月1日至2012年6月30日洛杉矶县高速公路环路探测器收集的交通信息。包含207个传感器,每5分钟采样一次。
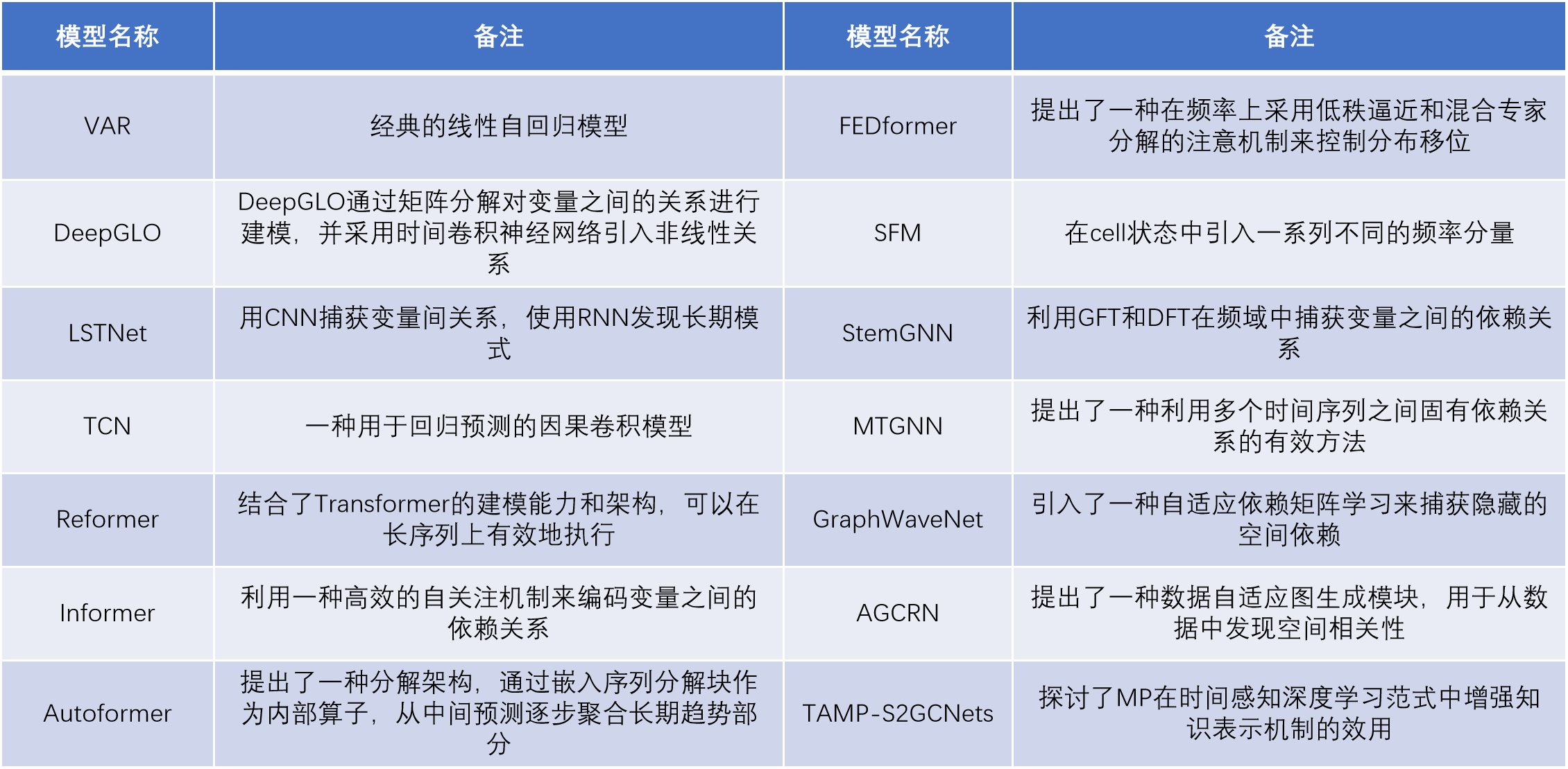
 2、基线方法
2、基线方法
3、实验结果
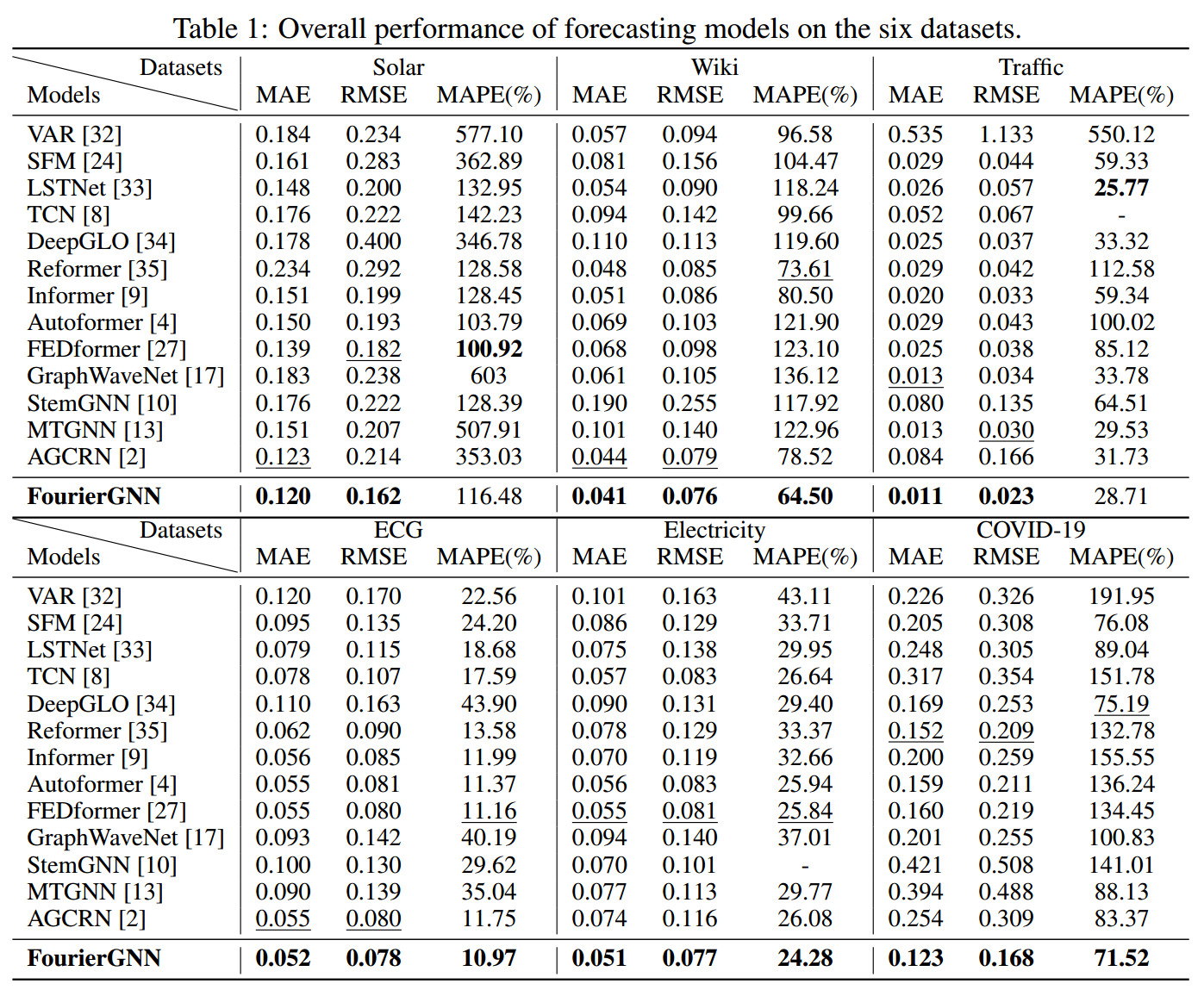 4、敏感性分析
4、敏感性分析
(1)针对预测长度不同的敏感性分析
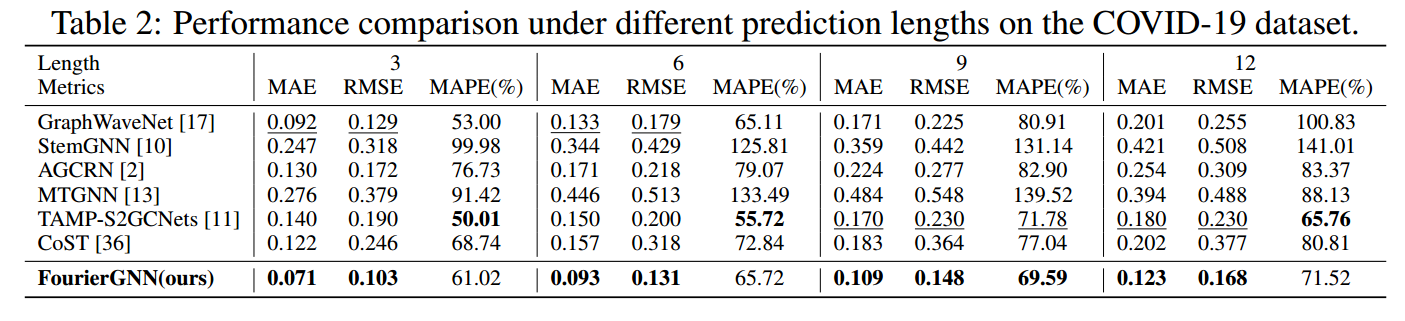
ECG数据集:
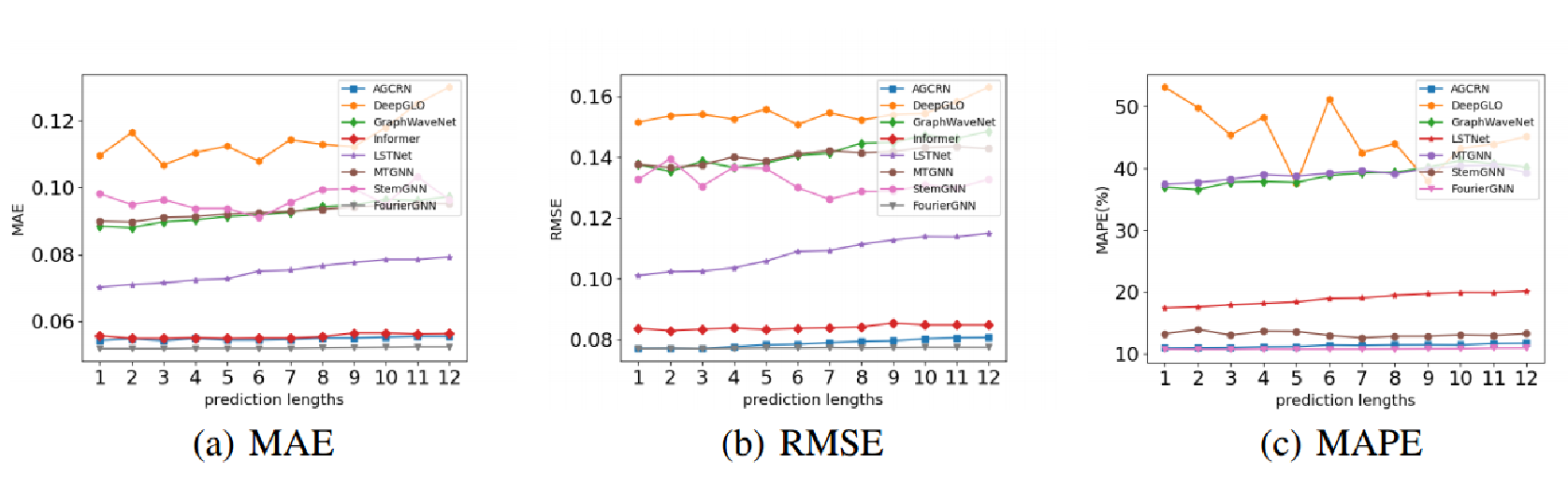
(2)针对节点数的敏感性分析
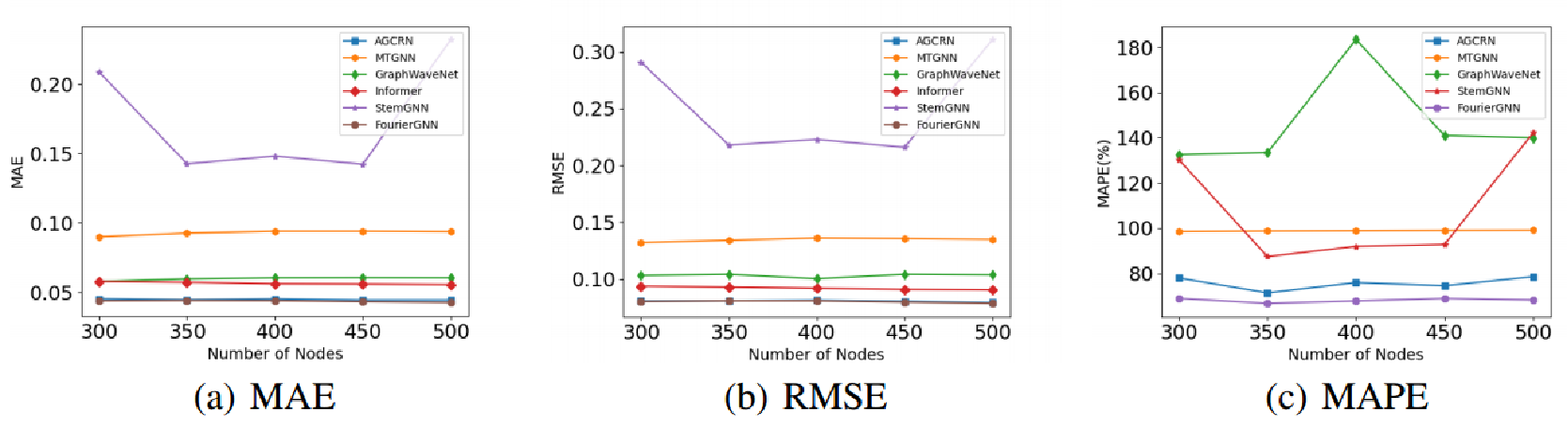 (3)针对不同扩散步的敏感性分析
(3)针对不同扩散步的敏感性分析
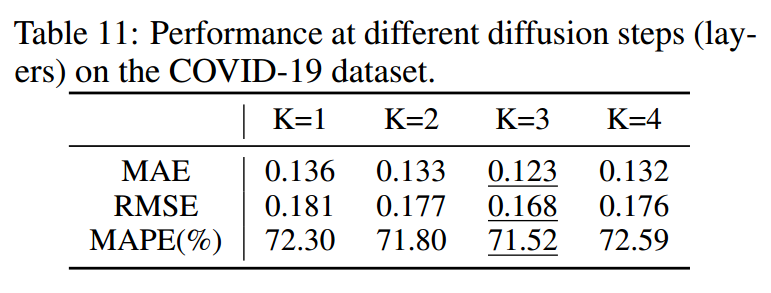
高阶扩散信息有利于提高预测精度,但随着阶数的增加,扩散信息的影响会逐渐减弱,甚至会给预测带来噪声
(4)针对输入窗口和嵌入维度的敏感性分析
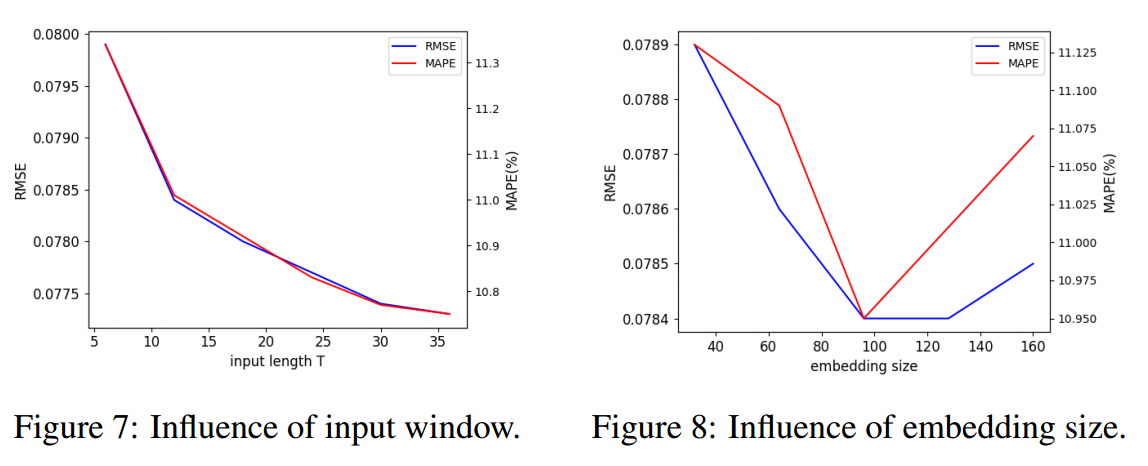 图7显示,随着输入回看窗口长度的增加,FourierGNN的性能(包括RMSE和MAPE)越来越好这表明FourierGNN可以从长MTS输入中学习到一个全面的超变量图,以捕获空间和时间依赖性。 图8显示,随着嵌入尺寸的增加,性能(RMSE和MAPE)先增加后降低,这是因为大的嵌入尺寸提高了FourierGNN的拟合能力,但也容易导致过拟合问题,尤其是当嵌入尺寸过大时。
图7显示,随着输入回看窗口长度的增加,FourierGNN的性能(包括RMSE和MAPE)越来越好这表明FourierGNN可以从长MTS输入中学习到一个全面的超变量图,以捕获空间和时间依赖性。 图8显示,随着嵌入尺寸的增加,性能(RMSE和MAPE)先增加后降低,这是因为大的嵌入尺寸提高了FourierGNN的拟合能力,但也容易导致过拟合问题,尤其是当嵌入尺寸过大时。
5、消融实验
(1) w/o Embedding: FourierGNN的一个变体将原始MTS输入而不是将其嵌入到傅里叶空间的图卷积中
(2) w/o Dynamic FGO: FourierGNN的一种变体对所有扩散步骤使用相同的FGO,而不是在不同的扩散步骤中应用不同的FGO它对应于一个普通的图过滤器。
(3) w/o Residual: FourierGNN的变体在求和中没有K = 0层输出,即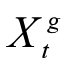
(4) w/o Summation: FourierGNN的一种变体采用最后一阶(层)输出作为FourierGNN的最终频率输出

6、可视化

将不同变量的时间邻接矩阵可视化 从COVID-19数据集中随机选择8个县,计算每个县连续12个时间步长的关系,可视化邻接矩阵 结果表明,FourierGNN在每个县学习到不同的时间模式,这表明该超变量图可以编码丰富的、有区别的时间依赖性。

将基于FourierGNN在METR-LA数据集上学习到的表示生成的邻接矩阵可视化
随机选择了20个检测器,并通过热图可视化它们对应的邻接矩阵 通过结合实际路线图检查邻接矩阵,我们观察到: (1) 探测器(7、8、9、11、13、18)在物理距离上非常接近,对应于它们在热图中相互关联的高值; (2) 探测器4、14、16距离其他探测器较远,整体相关值较小; (3) 与探测器14、16相比,探测器4与其他探测器如7、8、9的相关值略高,这是因为探测器4、7、8、9虽然相距较远,但在同一条路上 结果验证了超变量图结构可以表示高度可解释的相关性
六、总结
总结:
1、从纯图的角度直接应用图网络进行MTS预测
2、提出傅立叶图算子(Fourier graph Operator, FGO)叠加在傅立叶空间中进行矩阵乘法的傅立叶神经网络,该网络具有足够的学习表现力,且复杂度较低
3、FourierGNN以更高的效率和更少的参数实现了最先进的性能,并且超变量图结构表现出强大的编码时空相互依赖关系的能力
思考:
1、关于论文写作:作者的写作思路很顺利,从发现问题,到一步步解决问题,想法和做法都顺理成章,有很好的创新点
2、实验的丰富性:做了大量的对比实验,工作量很大,还附带有可解释性的图
3、从时域转到频域,注重学科交叉,将其他学科的知识应用到自己的领域,产生了很好的效果
源代码链接:
都看到这里了~给个小心心♥呗~