经典傅里叶变换的限制:
1、只能反映信号的整体特性;(完全是时域或频域)
2、要求信号满足平稳条件;
3、必须获得时域中的全部信息。
所以引入时频分析,同时使用时间和频率的联合函数来表示信号。
1 时频分析
1.1 短时Fourier变换
具体理论可以参看参考资料[1]的103~105页。
短时傅里叶变换的实现:
tfr,t,f\]=tfrstft(x) tfr为短时傅里叶变换的变换系数,t为系数tfr对应的时刻,f为归一化频率向量。 例1:构建一个有256个点的正弦信号x,在\[30,80\]区间的频率为32Hz,在\[140,190\]区间的频率为64Hz。fs=256Hz.用tfrstft对x进行时频分析。 clc; clear; fs=256; ts=1/fs; N=256; pt=0*ts:ts:(N-1)*ts; t1=zeros(N,1); t2=zeros(N,1); t1(30:80)=pt(30:80); t2(140:190)=pt(140:190); f1=32; f2=64; x=sin(2*pi*f1*t1)+sin(2*pi*f2*t2); figure(1); subplot(311) plot(pt,x); xlabel('time/s'); ylabel('幅值'); title('时域图') subplot(312) [tfr,t,f]=tfrstft(x); pcolor(t,f(1:N/2,1),abs(tfr([1:N/2],:))); colorbar; xlabel('采样点'); ylabel('归一化频率') title('时频分布') subplot(313) t=(t-1)/fs; f=f*fs; pcolor(t,f(1:N/2,1),abs(tfr([1:N/2],:))); xlabel('time/s'); ylabel('频率/Hz'); colorbar; 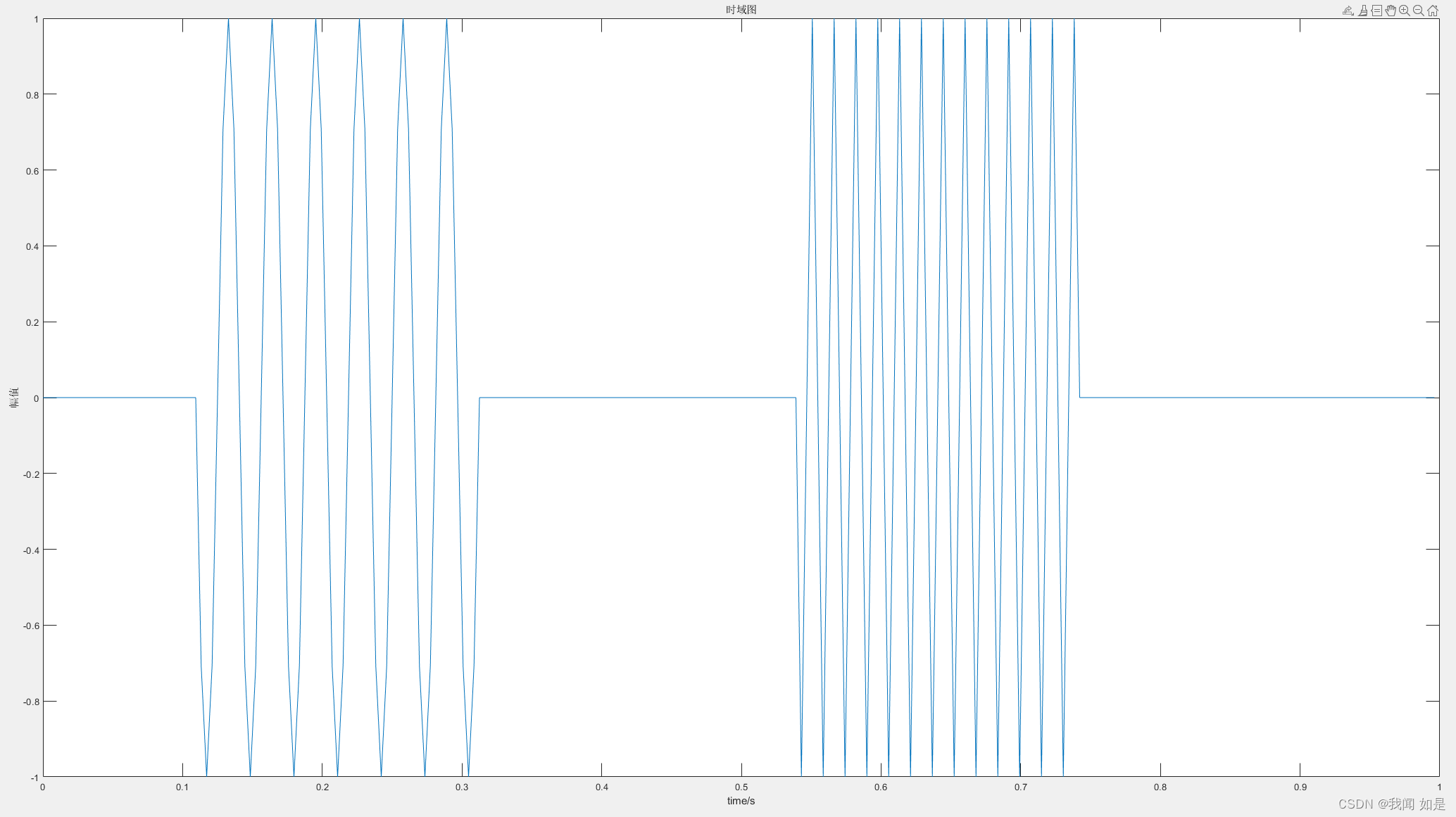  ### 1.2 Gabor变换 理论部分在参考资料\[1\]中110\~111. Gabor变换以高斯函数为窗函数。 选择高斯函数的原因:1、高斯函数的傅里叶变换仍为高斯函数;2、Gabor变换是最优的窗口Fourier变换。 **Gabor变换才是真正意义上的时间-频率分析。** Gabor变换的局限性:时间频率的宽度对所有频率是固定不变的。 matlab实现: \[tfr,dgr,gam\]=tfrgabor(x) \[tfr,dgr,gam\]=tfrgabor(x,N) N为Gabor系数的个数 \[tfr,dgr,gam\]=tfrgabor(x,N,Q) Q为过采样度。 例2 对信号进行gabor变换 clc; clear; fs=256; t=0:1/fs:1-1/fs; y=cos(20*pi.*t.*t)+cos(2*pi.*cos(6*pi.*t)+120*pi.*t); tfrgabor(y',64,32) 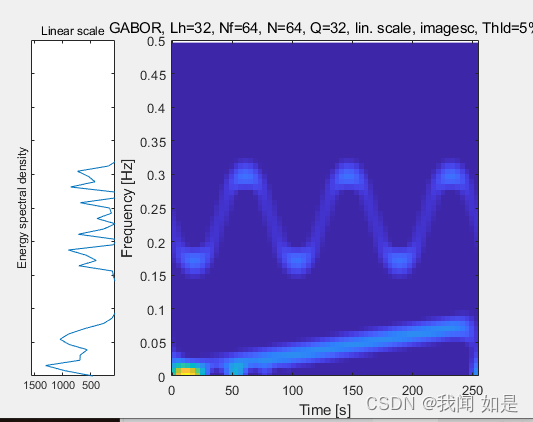 ### 1.3 Wigner-Ville时频分析 \[1\] 张玲玲 《基于matlab的机械故障诊断技术案例教程》