目录:
1.直接选择排序 的实现及分析
2.堆排序 的实现及分析
1.直接选择排序
1.1基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
1.2
一次排序-->将最大值放在第一个,最小值放在最后一个
代码实现:
#include<stdio.h>
void Swap(int* a, int* b)
{
int m = *a;
*a = *b;
*b = m;
}
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int min_i = begin, max_i = begin;
for (int i = begin; i <= end; i++)
{
if (a[i] < a[min_i])
{
min_i = i;
}
if (a[i] > a[max_i])
{
max_i = i;
}
}
Swap(&a[begin], &a[min_i]);
if (begin == max_i)
{
max_i = min_i;
}
Swap(&a[max_i], &a[end]);
++begin;
--end;
}
}
int main()
{
int arr[] = {23,45,99,0,1,14,689};
int n = sizeof(arr) / sizeof(int);
SelectSort(arr, n);
printf("最小值为:%d\n", arr[0]);
printf("最大值为:%d", arr[n - 1]);
return 0;
}测试结果:
1.3直接选择排序的特性总结:
直接选择排序思考非常好理解,但是效率不是很好,实际中很少使用。
时间复杂度:O(N^2)
空间复杂度:O(1)
稳定性:不稳定
2.堆排序 Heapsort
堆排序是利用堆 这种数据结构而设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
2.1什么是堆呢?
堆的逻辑结构是:一棵完全二叉树
物理结构是:一个数组
每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆
每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆

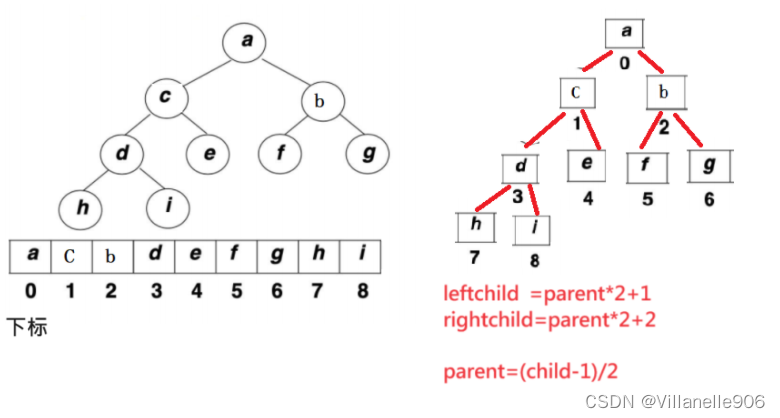
2.2向下调整算法
前提:该节点的左右子树都为 大/小堆
该算法就是将该节点与左右子树的节点进行比较,重新构建成一个大堆或者小堆。
例如:构建大堆 举例
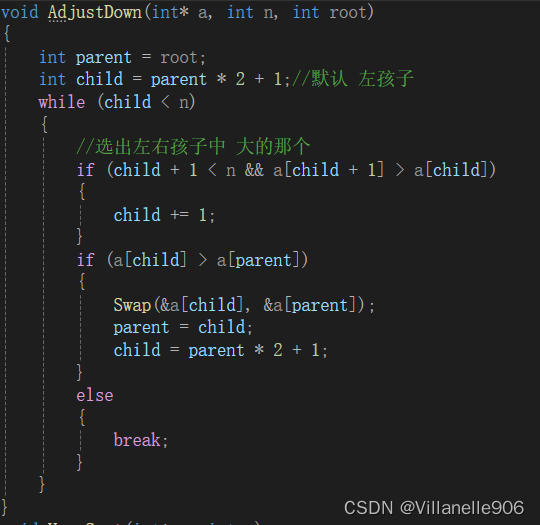
2.3 堆排序整体思路:(升序)-->大堆
对待排序的数组,先构建成 堆
从倒数第一个非叶子节点开始调整,把最大的换到最后,不把其看做是堆里的。前n-1个数向下调整,选出次大的数,再跟倒数第二个位置交换........
如此反复执行,便能得到一个有序序列

堆排序的特性总结:
堆排序使用堆来选数,效率就高了很多。
时间复杂度:O(N*logN)
空间复杂度:O(1)
稳定性:不稳定
代码实现:
#include<stdio.h>
void Swap(int* a, int* b)
{
int m = *a;
*a = *b;
*b = m;
}
void AdjustDown(int* a, int n, int root)
{
int parent = root;
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child + 1] > a[child])
{
child += 1;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int* a, int n)
{
//建堆 O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(a, n, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}
int main()
{
int arr[] = { 23,45,11,89,0,14,99 };
int n = sizeof(arr) / sizeof(int);
HeapSort(arr, n);
for (int i = 0; i < n; i++)
{
printf("%d ", arr[i]);
}
return 0;
}测试代码:
谢谢观看,希望对你有所帮助