机器学习(三)

机器学习

• • [3.5 决策树](#3.5 决策树)
  • • [3.5.1 认识决策树](#3.5.1 认识决策树)
    • [3.5.2 决策树分类原理](#3.5.2 决策树分类原理)
    • [3.5.3 决策树API](#3.5.3 决策树API)
    • [3.5.4 决策树可视化](#3.5.4 决策树可视化)
    • [3.5.5 鸢尾花案列](#3.5.5 鸢尾花案列)
    • • • [3.5.6 决策树总结](#3.5.6 决策树总结)
  • [3.6 集成学习方法之随机森林](#3.6 集成学习方法之随机森林)
  • • [3.6.1 什么是集成学习方法](#3.6.1 什么是集成学习方法)
    • [3.6.2 什么是随机森林](#3.6.2 什么是随机森林)
    • [3.6.3 随机森林原理过程](#3.6.3 随机森林原理过程)
    • [3.6.4 API](#3.6.4 API)
    • [3.6.5 总结](#3.6.5 总结)
• 4.回归和聚类算法
• • [4.1 线性回归](#4.1 线性回归)
  • • [4.1.1 线性回归的原理](#4.1.1 线性回归的原理)
    • [4.1.2 线性回归的损失和优化原理](#4.1.2 线性回归的损失和优化原理)
  • [4.2 欠拟合与过拟合](#4.2 欠拟合与过拟合)
  • • [4.2.1 定义](#4.2.1 定义)
    • [4.2.2 原因以及解决方法](#4.2.2 原因以及解决方法)
    • [4.2.3 正则化](#4.2.3 正则化)

3.5 决策树

3.5.1 认识决策树

决策树思想的来源非常朴素，程序设计中的条件分支结构就是if-else结构，最早的决策树就是利用这类结构分割数据的一种分类学习方法。

那我们应该把那个作为条件放在第一个分支呢？也就是说我们如何去判断特征的先后顺序，接着往下看。

3.5.2 决策树分类原理

1. 信息量用信息熵来衡量（单位为bit）

   

2. 决策树的划分依据之一------信息增益

   • 定义与公式

     特征A对训练数据集D的信息增益g(D,A)定义为集合D的信息熵H(D)与特征A给定条件下D的信息条件熵H(D|A)之差，即公式为：

     

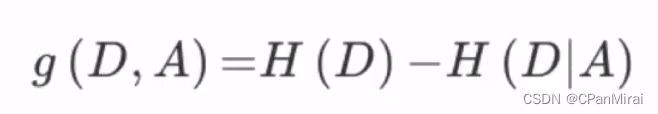
3. 公式详解：

• 信息熵的计算：

  

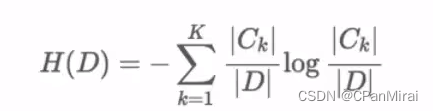
• 条件熵的计算：

  

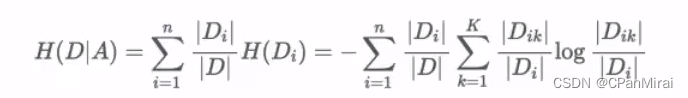
注：Ck表示属于某个类别的样本数。

信息增益表示得知特征X的信息而使得类Y的信息熵减少的程度。

4. 决策树的其他划分依据
   • ID3 信息增益 最大的准则
   • C4.5 信息增益比 最大的准则
   • CART
     • 分类树：基尼系数 最小的准则 在sklearn中可以选择划分的默认原则
     • 优势：划分更加细致

3.5.3 决策树API

# 决策树分类器
sklearn.tree.DecisionTreeClassifier(criterion = 'gini',max_depth = None,random_state = None)
	# criterion : 默认是'gini'系数，也可以选择信息增益的熵'entropy'
    # max_depth : 树的深度大小，不能太深，否则就是出现过拟合现象，在训练数据上很厉害，在测试集上效果不佳，换句话说，太专用了，没有那么兼容
    # random_state : 随地数种子 

3.5.4 决策树可视化

sklearn.tree import export_graphviz(estimator, out_file="iris.dot", feature_names=iris.feature_names)

3.5.5 鸢尾花案列

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz


def decision_tree():
    """
    决策树对鸢尾花进行分类
    :return:
    """
    # 1.获取数据
    iris = load_iris()
    # 2.划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=10)
    # 4.模型训练
    estimator = DecisionTreeClassifier(criterion="entropy")
    estimator.fit(x_train, y_train)
    # 5.模型评估
    # 5.1 直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("预测值是：", y_predict)
    print("直接比对真实值和预测值：", y_test == y_predict)
    # 5.2 计算准确率
    print("测试集的准确率是：", estimator.score(x_test, y_test))
    # 6.决策树可视化
    export_graphviz(estimator, out_file="iris.dot", feature_names=iris.feature_names)
    return None


if __name__ == '__main__':
    decision_tree()

iris.dot里面文件不是很好懂，我们借助于http://www.webgraphviz.com/网址，然后把iris.dot文件内容复制到对话框中去，点击生成图表即可。

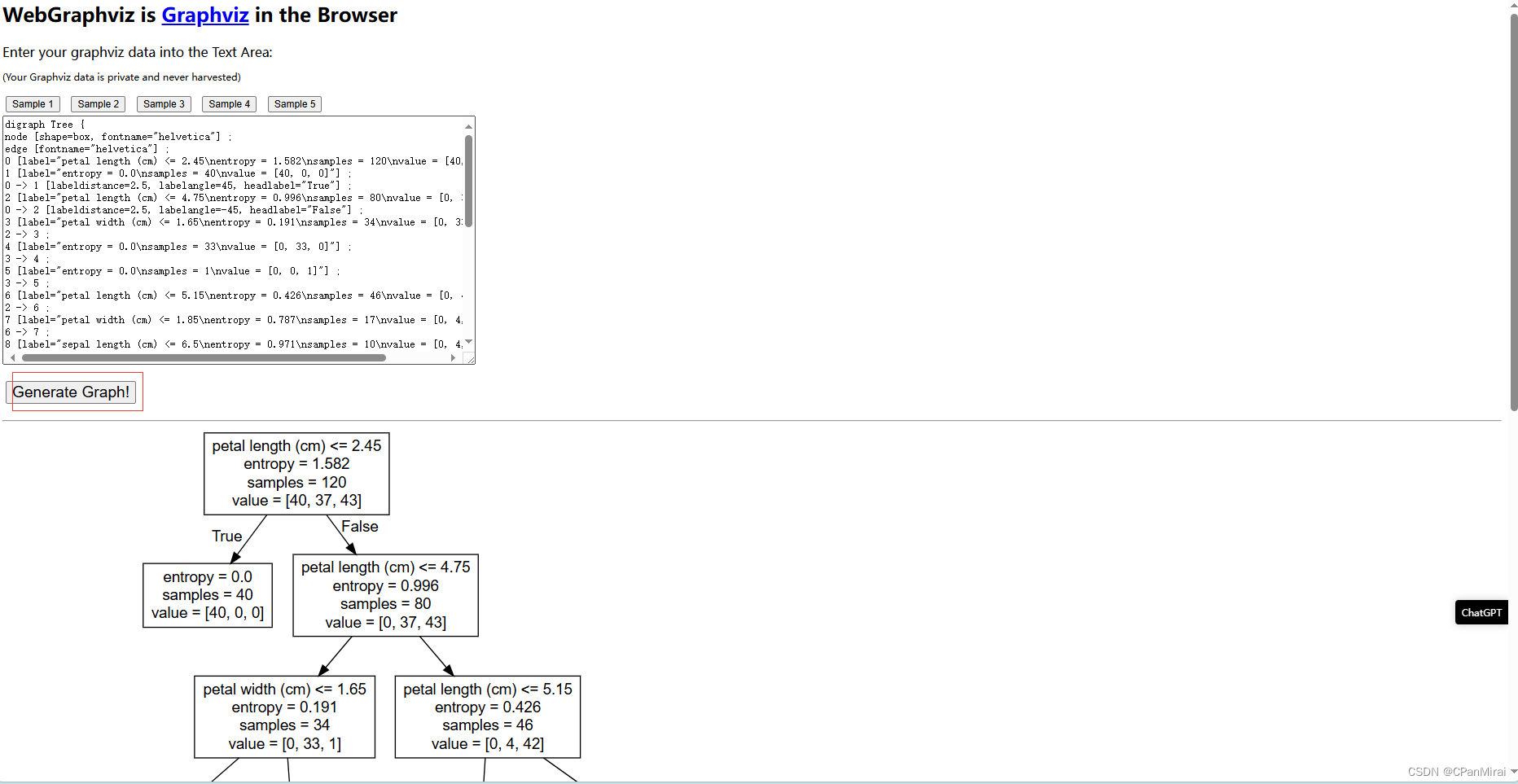
3.5.6 决策树总结

• 优点：简单的理解和解释，树木可视化。
• 缺点：决策树树的深度控制不好，就会过拟合现象。
• 改进：
  • 剪枝cart算法（决策树API当中已经实现）
  • 随机森林

3.6 集成学习方法之随机森林

3.6.1 什么是集成学习方法

集成学习通过几个模型组合来解决单一预测问题。它的工作原理是生成多个分类器/模型，各自独立地去学习和做出预测。这些预测最后结合成组合预测，因此优于任何一个单分类的做出预测。

3.6.2 什么是随机森林

在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别数输出的类别的众数而定。

3.6.3 随机森林原理过程

根据下列算法而建造每棵树：

• 用N表示训练用例(样本)的个数，M表示特征数目。
  • 一次随机选出一个样本，重复N次。（有可能出现重复的样本）
  • 随机的去选出m个特征，m << M,建立决策树。（有特征降维的效果）
• 采用bootstrap抽样

为什么采用BootStrap抽样？

• 为什么要随机抽样训练集？
  • 如果不进行随机抽样，每棵树的训练集都一样，那么最终训练出的树分类结果也是完全一样的。
• 为什么要有放回的抽样？
  • 如果不是有放回的抽样，那么每棵树的训练样本都是不同的，每颗树训练出来都是由很大的差异的；而随地森林最后分类取决于多颗树的投票结果。

3.6.4 API

# 随机森林分类器
class sklearn.ensemble import RandomForestClassifier(n_estimators = 100,criterion = 'gini',max_depth = None,min_samples_split = 2,bootstrap = true,random_state = None)
	# 列举是常用的参数，其他的可以看源码
    # n_estimators : int, default=100 The number of trees in the forest.
    # criterion : {"gini", "entropy", "log_loss"}, default="gini" 分割特征的测量方法
    # max_depth : int, default=None 
    # min_samples_split : int or float, default=2
    # bootstrap : bool, default=True 在构建树时需要方法抽样
    # random_state : int, RandomState instance or None, default=None

3.6.5 总结

• 在当前所有算法中，具有极好的准确率
• 能够有效地运行在大数据集上，处理具有高维特征的输入样本，而且不需要降维
• 能够评估各个特征在分类问题上的重要性

4.回归和聚类算法

4.1 线性回归

4.1.1 线性回归的原理

1. 线性回归应用场景

   • 房价预测
   • 销售额度预测
   • 贷款额度预测

2. 什么是线性回归

   • 定义与公式

     • 线性回归（Linear regression）是利用回归方程(函数)对一个或多个自变量（特征值）和因变量（目标值）之间关系进行建模的一种分析方式。

       • 特点：只有一个自变量的情况称为单变量回归，多于一个自变量情况的叫做多元回归。

         

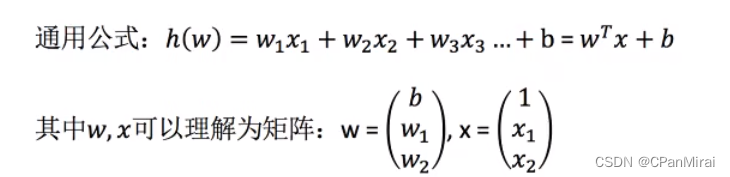
   • 线性回归当中线性模型有两种，一种是线性关系，另一种是非线性关系。

     • 线性关系

       
       

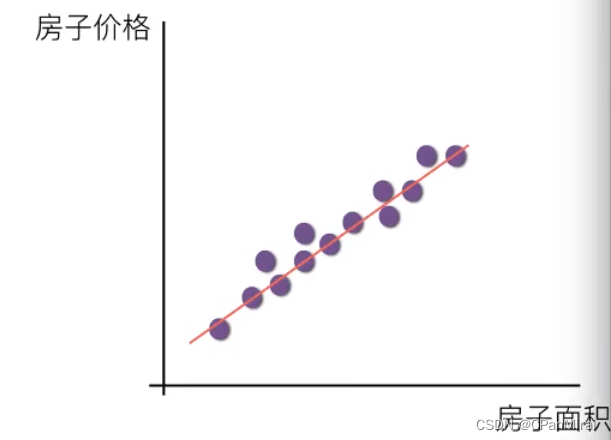
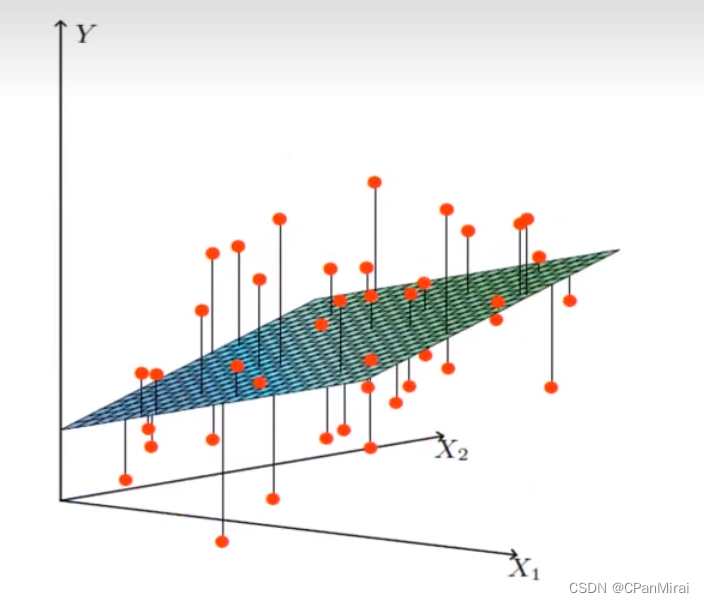
       注：单特征与目标值的关系呈现直线关系，两个特征与目标值呈现平面的关系。

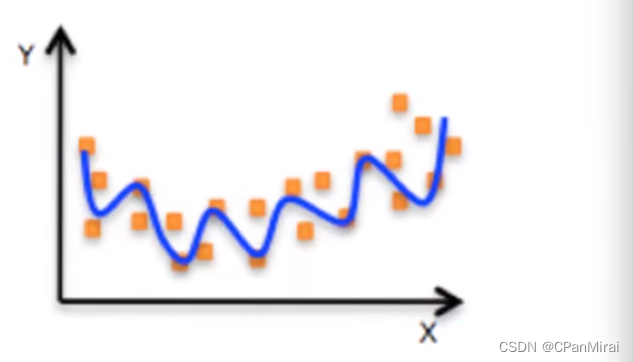
     • 非线性关系(可以理解为 W1*X1 + W2X2^2+W3*X3^3+b)
       

4.1.2 线性回归的损失和优化原理

真实的线性关系和我们预测的线性关系存在一定误差，那么存在，我们需要把这个误差进行衡量出来（使用损失函数 ），我们想办法去减少误差，去修正（优化损失），不断地去逼近真实的线性关系,从而预测的结果更加准确。

1. 损失函数（最小二乘法）：

   

2. 优化损失

   如何去求模型当中的W,使得损失最小？（目的是找到最小损失对应的W值）

   线性回归中经常用两种优化算法：

   • 正规方程（直接求解得到W，使用高数里面求最小值的方法，进行求导）

     

   • 梯度下降(不断试错，最终找到合适的)

4.2 欠拟合与过拟合

4.2.1 定义

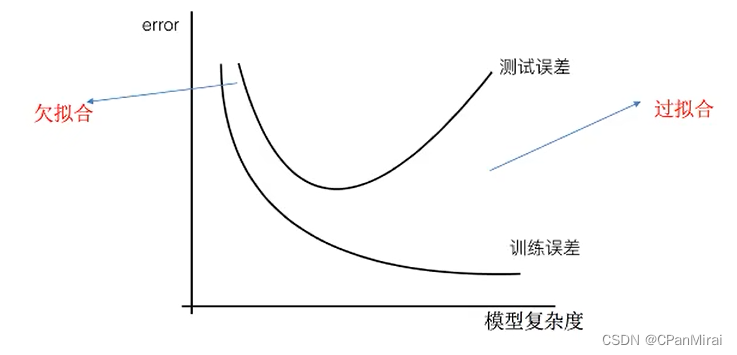
欠拟合：一个假设在训练数据上不能获得更好的拟合，并且在测试数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。（模拟过于简单）

过拟合：一个假设在训练数据上能够很好的拟合，但是在测试数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。（模型过于复杂）

4.2.2 原因以及解决方法

• 欠拟合原因以及解决方法
  • 原因：学习到数据的特征过少
  • 解决方法：增加数据的特征数量
• 过拟合原因以及解决办法
  • 原因：原始特征过多，存在一些嘈杂特征，模型过于复杂，因为模型尝试去兼顾各个测试数据点。
  • 解决方法：正则化

​ 如何解决 ?

4.2.3 正则化

• L2 正则化

  • 作用：可以使得其中一些W的都很小，都接近于0，削弱某个特征的影响。

  • 优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象。

  • 加入L2正则化后的损失函数（Ridge回归）：

    

• L1正则化

  • 作用：可以使得其中一些W的值直接为0，删除这个特征的影响。
  • LASSO回归