文章目录
深度学习概述
前文提到深度学习分三步:神经网络 -- 衡量方程优劣 -- 找出最好的方程。我们这节就围绕神经网络展开。
神经网络简介

神经网络的网络结构由多个神经元组成,不同的连接导致不同的结构。
如下图,这是一个网络结构示例:


不难得出,一个网络结构实际是定义了一个方程组。
比如图中的两个例子,在这个网络输入不同的值,计算得出不同的输出。这本质就是一个方程组 f([1, -1])=[0.62, 0.83], f([0, 0])=[0.51, 0.85]。
对于一个完整的神经网络,可以分成如下三层:输入层、隐层、输出层。

损失函数

对于一组给定参数,经过隐层计算后得到输出向量 y y y。此时,利用 y y y, y ^ \hat{y} y^ 这两个向量计算交叉熵。

对所有的训练数据计算出的所有交叉熵,计算总损失 L L L。通过计算总损失,可以找到使总损失最小的方程和网络参数。
反向传播
反向传播为了实现参数的最优化,进而优化神经网络。

在反向传播中,输出与期望的误差的平方和作为目标函数,转入反向传播,逐层求出目标函数对各神经元权值的偏导数,构成目标函数对权值向量的梯量,作为修改权值的依据。
总结,记住反向传播是利用计算梯度来优化神经网络即可。
卷积神经网络
什么是卷积神经网络
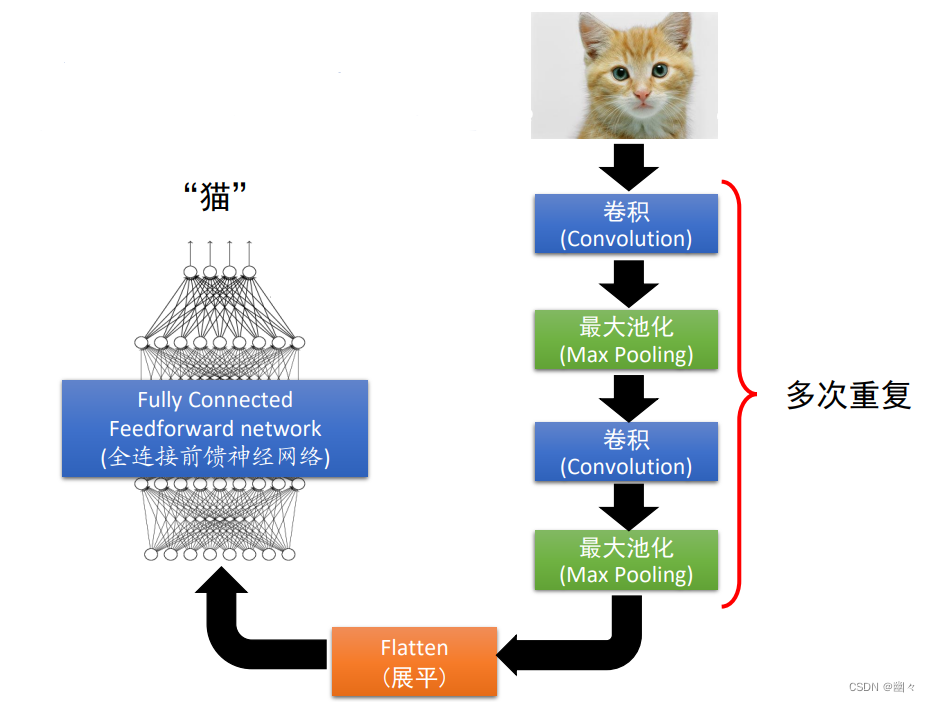
这张图展示了一个卷积神经网络的流程------对一个输入进行多次卷积和最大池化,在展平之后交给全连接前馈神经网络。
卷积

对于一个图像,我们首先把他转化成二维矩阵的形式。此时,有 n 个如图所示的小矩阵被称为卷积核。每个卷积核检测一个模式(3 * 3)。意思就是这里一个卷积核只有3*3大小,只能检测这么大。

用第一个矩阵,卷积核 1 来举例。
首先从图像矩阵左上角开始,取 3*3 大小的部分,和该卷积核做点乘运算,得到值 3。
左上角那个3*3大小的矩阵和卷积核1矩阵,内部每个对应位置的元素相乘,然后相加得到结果。
可以看到步长为 1,所以我们将这个 3*3 的小框向右平移 1 格,再次点乘运算,得到值 -1。
如果步长为2,那么一次平移2格。

可以看到过完整个图像矩阵后得到的结果如图所示。

对每个过滤器(卷积核)做同样的处理,得到 n 个 4*4 图像。
红框用的是卷积核1,蓝框用的是卷积核2。
这样,我们就把一个彩色图像转换成了特征图,这样的好处是减少了参数。
最大池化

拿上文中的卷积核 2(蓝框)得到的特征图来进行说明。
我们可以直观地理解为,对于每个 2*2 的窗口,取其中的最大值,这样可以取特征中最强烈的部分进入下一层,去掉冗余信息。
反复的重复卷积操作和最大池化操作,可以得到一张更小的图像。
每一个卷积核实际上是一个通道,通道的个数就是卷积核的个数。通道就是什么RGB通道啊之类的
展平

字面意思,把每个特征图矩阵展平成输入。
典型的神经网络结构
主要记一下顺序和长什么样就行


(1)使用了 ReLU 激活函数: f(x)=max(0,x)
(2)标准化
(3)有效地防止神经网络的过拟合
(4)数据增广




Transformer(转换器、变压器?)
自注意力机制
- Step 1:

首先输入一组 { x 1 , x 2 , x 3 , x 4 } \{x_1, x_2, x_3, x_4\} {x1,x2,x3,x4},他们分别与权重矩阵 W W W 相乘得到向量 { a 1 , a 2 , a 3 , a 4 } \{a_1, a_2, a_3, a_4\} {a1,a2,a3,a4}。
这些向量分别与不同的变换矩阵 { W q , W k , W v } \{W^q, W^k, W^v\} {Wq,Wk,Wv} 相乘,得到三个向量,记为 { q i , k i , v i } \{q^i, k^i, v^i\} {qi,ki,vi}。其中 q i q^i qi 用来匹配单词; k i k^i ki 为密钥,被 q i q^i qi 匹配; v i v^i vi 则是被抽出的信息。 - Step 2:

q 1 q^1 q1 和 k i k^i ki 遍历做运算,得到 α 1 , i \alpha_{1,i} α1,i 。其中, d d d 是 q q q 和 k k k 的维数,除以 d \sqrt{d} d 是为了消除点乘带来的常数放大。 - Step 3:

将这些 α 1 , i \alpha_{1,i} α1,i 作为输入 Soft-max 函数,得到输出 α ^ 1 , i \hat\alpha_{1,i} α^1,i。
Soft-max 函数被称为归一化指数函数,计算方法如图片上方公式所列出。exp 指自然指数函数。 - Step 4:

上一步得到的 α ^ 1 , i \hat\alpha_{1,i} α^1,i,分别与各自的 v i v^i vi 相乘,得到 b 1 b^1 b1。
同理,算出 α ^ 2 , i \hat\alpha_{2,i} α^2,i,分别与各自的 v i v^i vi 相乘,得到 b 2 b^2 b2。

这一步的 b i b^i bi 是可以并行计算的。
综上,这几步可以概括为:计算 q i q^i qi, k i k^i ki, v i v^i vi;计算 α j , i \alpha_{j, i} αj,i;计算 α ^ j , i \hat\alpha_{j, i} α^j,i;计算 b j b^j bj。
将这个过程转化成矩阵表示如下:

多头注意力机制
