【Python实战因果推断】8_元学习器3

[Metalearners for Continuous Treatments](#Metalearners for Continuous Treatments)

Metalearners for Continuous Treatments

一如既往，当干预是连续性的，事情就会变得有点复杂。元学习器也不例外。作为一个运行示例，让我们使用上一章中的数据。回想一下，它包含了一家连锁餐厅三年的数据。该连锁店对旗下六家餐厅随机打折，现在它想知道哪天是给予更多折扣的最佳时机。要回答这个问题，就需要了解顾客在哪天对折扣更敏感（对价格更敏感）。如果连锁餐厅能够了解这一点，他们就能更好地决定何时给予更多或更少的折扣。

如您所见，这是一个需要估算 CATE 的问题。如果您能做到这一点，公司就可以利用您的 CATE 预测来决定折扣政策--预测的 CATE 越高，顾客对折扣越敏感，因此折扣应该越高：

python 复制代码

 data_cont = pd.read_csv("./data/discount_data.csv")
 data_cont.head()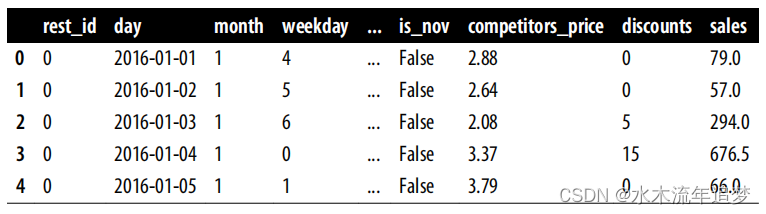

在这个数据中，折扣是干预，销售是结果。您还有一些经过设计的日期特征，如月份、星期几、是否是节假日等。由于这里的目标是 CATE 预测，因此最好将数据集分为训练集和测试集。分为训练集和测试集。

python 复制代码

 train = data_cont.query("day<'2018-01-01'")
 test = data_cont.query("day>='2018-01-01'")

现在大家已经熟悉了这些数据，让我们看看哪些元学习器可以干预这种连续处理。

S-Learner

您应该尝试的第一个学习器是 S 学习器。这是最简单的学习器。你将使用一个单一的（因此是 S）机器学习模型来进行估计：

为此，您将把干预作为一个特征纳入试图预测结果 Y 的模型中：

python 复制代码

 X = ["month", "weekday", "is_holiday", "competitors_price"]
 T = "discounts"
 y = "sales"
 np.random.seed(123)
 s_learner = LGBMRegressor()
 s_learner.fit(train[X+[T]], train[y]);

但该模型并不直接输出干预效果。相反，它输出的是反事实预测。也就是说，它可以在不同的干预制度下做出预测。如果干预是二元的，这个模型仍然有效，试验和对照之间的预测差异将是 CATE 估计值：

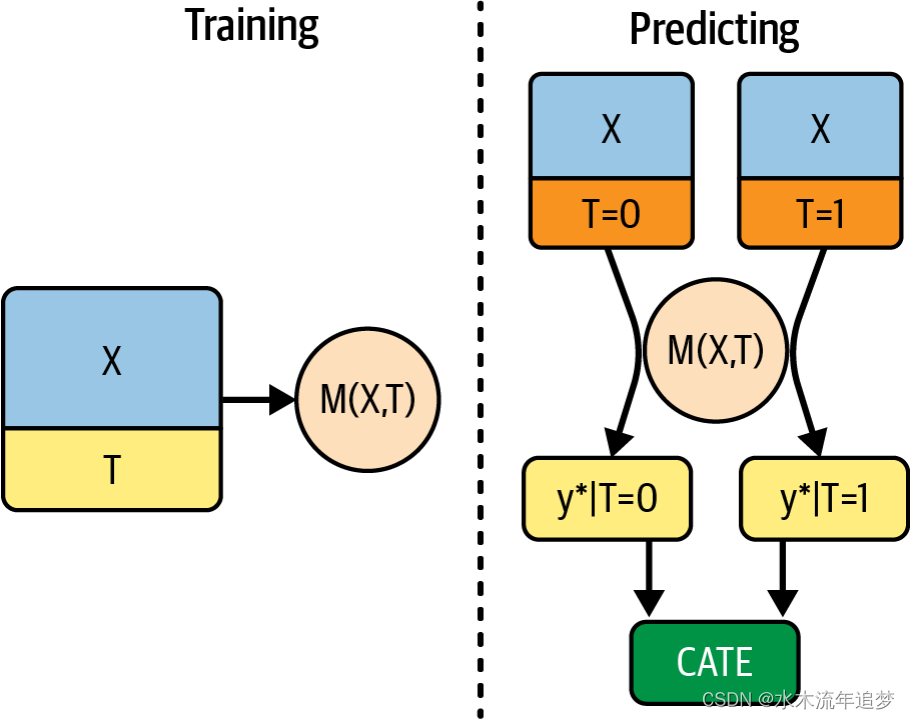在连续情况下，您需要做一些额外的工作。首先，您需要定义一个干预网格。在示例中，折扣从 0 到 40% 左右，因此可以尝试使用 [0, 10, 20, 30, 40] 网格。接下来，您需要扩展要进行预测的数据，这样网格中的每个干预值每行都会得到一个副本。我能找到的最简单的方法是将包含网格值的数据帧交叉连接到要进行预测的数据中--测试集。在 pandas 中，你可以使用常量键进行交叉连接。这将复制原始数据中的每一行，只改变干预值。最后，您可以使用拟合的 S-learner 在此扩展数据中进行反事实预测。下面是一段简单的代码，可以完成所有这些工作：

python 复制代码

 t_grid = pd.DataFrame(dict(key=1,
 discounts=np.array([0, 10, 20, 30, 40])))
 test_cf = (test
 .drop(columns=["discounts"])
 .assign(key=1)
 .merge(t_grid)
 # make predictions after expansion
 .assign(sales_hat = lambda d: s_learner.predict(d[X+[T]])))
 test_cf.head(8)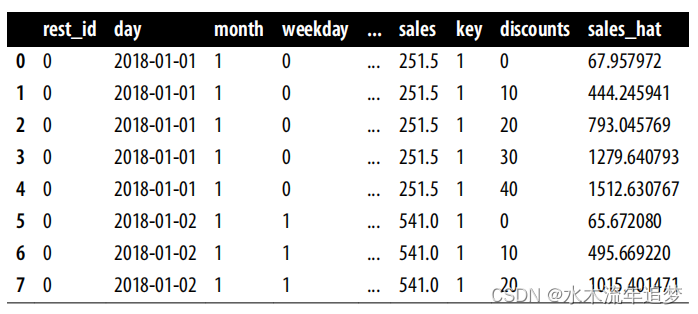

在上一步中，您基本上已经估算出了每个单元的粗略版干预反应函数。您甚至可以绘制一些单位（在我们的案例中是天数）的曲线，看看它们是什么样子的。在下图中，您可以看到 2018-12-25 日（即圣诞节）的估计响应函数比 2018-06-18 日这样的日子的响应函数更陡峭 。这意味着您的模型了解到，与 6 月份的那一天相比，顾客对圣诞节的折扣更加敏感 ：

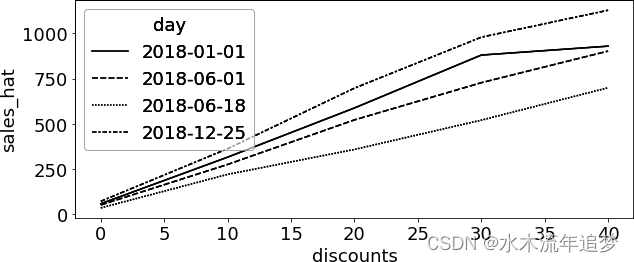
至于这些反事实预测是否正确，则是另外一个问题了。要对这个模型进行评估，首先要认识到我们仍然没有 CATE 预测。这意味着您学到的评估方法不能在这里使用。为了得到 CATE 预测值，您必须以某种方式将单位水平曲线总结为一个代表干预效果的数字。令人惊讶的是，线性回归是一个很好的方法。简单地说，您可以对每个单位进行回归，提取干预的斜率参数作为 CATE 估计值。

由于您关心的只是斜率参数，因此可以使用单变量线性回归的斜率公式更有效地完成这项工作：

让我们来看看实现这一目标的代码。首先，我定义了一个函数，将每条曲线汇总为一个斜率参数。然后，我按餐厅 ID 和日期对扩展测试数据进行分组，并将斜率函数应用到每个单位。这样就得到了一个以 rest_id 和 day 为索引的 pandas 序列。我将其命名为 cate。最后，我将该序列与原始测试集（而非扩展后的测试集）进行连接，以获得测试集中每一天和每一家餐厅的 CATE 预测值：

python 复制代码

 from toolz import curry
 @curry
 def linear_effect(df, y, t):
 return np.cov(df[y], df[t])[0, 1]/df[t].var()
 
 cate = (test_cf
 .groupby(["rest_id", "day"])
 .apply(linear_effect(t="discounts", y="sales_hat"))
 .rename("cate"))
 test_s_learner_pred = test.set_index(["rest_id", "day"]).join(cate)
 test_s_learner_pred.head()

现在您已经有了一个CATE预测，您可以使用从上一章学习到的方法来验证您的模型。在这里，让我们坚持使用累积收益：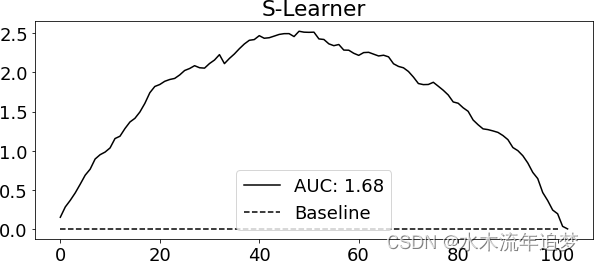

从累积增益可以看出，S-learner 虽然简单，但在这个数据集上的表现还不错。同样，请记住，这种表现对这个数据集来说非常特殊。这是一个特别简单的数据集，因为你有很多随机数据，甚至可以用它们来训练你的学习器。在实践中，我发现对于任何因果问题，S 学习器都是一个很好的首选，这主要是因为它很简单。即使没有随机数据进行训练，它的表现也往往不错。此外，S-learner 既支持二元干预，也支持连续干预，因此是一个很好的默认选择。

S-learner 的主要缺点是它倾向于将干预效果偏向零。由于 S-learner 采用的通常是正则化的机器学习模型，因此正则化会限制估计的干预效果。

下图复制了 Chernozhukov 等人的论文《治疗效果的双重/偏差/奈曼机器学习》中的结果。为了绘制这幅图，我模拟了包含 20 个协变量和二元干预的数据，其真实 ATE 为 1。我重复了 500 次模拟和估计步骤，并绘制了估计 ATE 与真实 ATE 的分布图：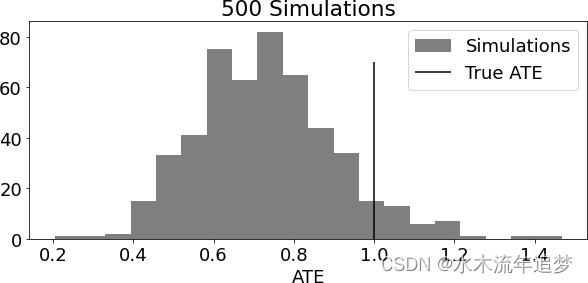

可以看出，估计 ATE 的分布集中在真实 ATE 的左侧，偏向于零。换句话说，真实的因果效应往往大于估计的因果效应。

更糟糕的是，如果相对于其他协变量对干预结果的解释作用而言，治疗效果非常弱，S-learner 可以完全舍弃治疗变量 。请注意，**这与您所选择的 ML 模型有很大关系。正则化程度越高，问题就越大。**Chernozhukov 等人在同一篇文章中提出了一种解决方法，即双偏差机器学习（Double/Debiased Machine Learning）或 R-learner。