【论文阅读】-- M4：面向可视化的时间序列数据聚合

M4: A Visualization-Oriented Time Series Data Aggregation

- 摘要
- [1 引言](#1 引言)
- [2. 查询重写](#2. 查询重写)
- 3.时间序列可视化
- [4. 数据缩减运算符](#4. 数据缩减运算符)
- - [4.1 面向可视化的数据聚合](#4.1 面向可视化的数据聚合)
  - [4.2 M4聚合](#4.2 M4聚合)
  - [4.3 聚合相关的像素错误](#4.3 聚合相关的像素错误)
  - [4.4 M4 上限](#4.4 M4 上限)
- [5. 时间序列数据缩减](#5. 时间序列数据缩减)
- [6. 评估](#6. 评估)
- - [6.1 真实世界时间序列数据](#6.1 真实世界时间序列数据)
  - [6.2 查询执行性能](#6.2 查询执行性能)
  - [6.3 可视化质量和数据效率](#6.3 可视化质量和数据效率)
  - [6.4 像素误差评估](#6.4 像素误差评估)
  - [6.5 数据减少潜力](#6.5 数据减少潜力)
- [7. 相关工作](#7. 相关工作)
- - [7.1 可视化系统](#7.1 可视化系统)
  - [7.2 数据缩减](#7.2 数据缩减)
  - [7.3 可视化驱动的数据缩减](#7.3 可视化驱动的数据缩减)
- [8 结论](#8 结论)
- 参考文献

期刊: Proc. VLDB Endow. （发表日期: 2014 ）
作者: Uwe Jugel; Zbigniew Jerzak; Gregor Hackenbroich; Volker Markl

摘要

对大量时间序列数据的可视化分析在许多行业中都很普遍，包括金融、银行和离散制造。用于大容量时间序列数据可视化的当代基于 RDBMS 的系统难以应对交互式可视化的硬延迟要求和高摄取率。现有的减少时间序列数据量的解决方案忽视了可视化的语义并导致可视化错误。

在这项工作中，我们介绍了 M4，一种基于聚合 的时间序列降维技术 ，可以以高数据缩减率提供无错误的可视化。我们重点关注作为时间序列可视化的主要形式的折线图，通过尊重线光栅化的过程，详细解释了现有数据缩减技术的缺点以及我们的方法如何超越现有技术。

我们描述了如何在可视化驱动的查询重写系统中在查询级别合并基于聚合的降维。我们的方法是通用的，适用于任何使用 RDBMS 作为数据源的可视化系统。使用来自高科技制造、股票市场和体育分析领域的现实世界数据集，我们证明了面向可视化的数据聚合可以将数据量减少多达两个数量级，同时保持完美的可视化。

关键词：关系数据库、查询重写、降维、线栅格化

1 引言

企业正在公共云和私有云中收集 PB 级的数据，其中的时间序列数据来自各种来源，包括传感器网络 [15]、智能电网、金融市场等等。大量收集的时间序列数据随后存储在关系数据库中。关系数据库又被可视化数据分析工具用作后端。数据分析师与可视化进行交互，他们的操作被可视化数据分析工具转换为针对关系数据库发出的一系列查询，并保存原始时间序列数据。在最先进的可视化分析工具中，例如 Tableau、QlikView、SAP Lumira 等，向数据库发出此类查询时不考虑查询结果的基数。然而，当从大容量数据源读取数据时，结果集通常包含数百万行。这导致可视化系统和数据库之间的带宽消耗非常高。

让我们考虑下面的例子。高科技制造业的 SAP 客户报告称，100 名工程师同时访问包含设备监控数据的全球数据库并不罕见。此类监控数据源自嵌入高科技制造机器中的传感器。此类嵌入式传感器的常见报告频率是 100Hz [15]。工程师通常会访问任何给定传感器过去 12 小时内的数据。如果可视化系统使用非聚合查询，例如

SELECT time,value FROM sensor WHERE time > NOW()-12*3600

为了从数据库中检索必要的数据，要传输的数据总量为 100 个用户·(12·3600)秒·100Hz = 4.32 亿行，即每个可视化客户端超过 400 万行。假设每行的线路大小为 60 字节，则需要从数据库传输到所有可视化客户端的数据总量几乎为 26GB。每个用户都必须等待近 260MB 的数据加载到可视化客户端，然后才能检查显示传感器信号的图表。

随着高频数据源和实时可视化系统的激增，SAP 不仅在高科技制造业，而且在越来越多的行业（包括体育分析）中观察到上述并发使用模式及其影响 [22] 、金融和公用事业。

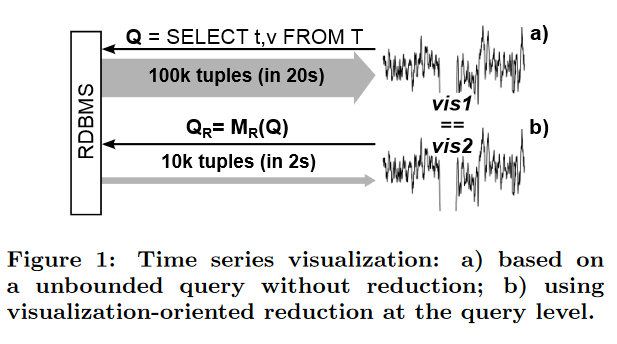
呈现给工程师的最终可视化本质上仅限于使用宽度×高度像素（结果图表的区域）显示检索到的数据。这意味着可视化系统必须执行数据缩减，将接收到的结果集转换并投影到宽度×高度栅格上。这种减少由可视化客户端隐式执行，并应用于所有结果集，无论它们包含多少行。本文的目标是利用这一基本观察结果并在数据库的查询级别应用适当的数据缩减。如图 1 所示，目标是使用数据缩减运算符 MR 重写与可视化相关的查询 Q，以便生成的查询 QR 生成小得多的结果集，而不会损害生成的可视化。数据量的显着减少缓解了高网络带宽要求，并缩短了可视化系统用户的等待时间。请注意，我们方法的目标不是计算数据库内的图像，因为这会阻止客户端与数据的交互。相反，我们的系统应该选择原始结果集的子集，这些子集可以被任何可视化客户端透明地使用。

为了实现这些目标，我们提出以下贡献。我们首先提出一种可视化驱动的查询重写技术，依赖于关系运算符并用所需可视化的宽度和高度进行参数化。其次，关注折线图的详细语义，作为时间序列可视化的主要形式，我们开发了一种可视化驱动的聚合，仅选择绘制完整基础数据的正确可视化所需的数据点。因此，我们通过选择每个时间间隔（对应于最终可视化中的像素列）、具有最小值和最大值的元组以及具有最小和最大时间戳的第一个和最后一个元组来对可视化过程进行建模。像素列。据我们所知，文献中没有对该数据缩减模型的应用或先前的讨论，尽管它为线路可视化提供了出色的结果。在本文中，我们弥补了这一缺点，并解释了在线光栅化背景下所选的最小值、最大值以及附加的第一个和最后一个元组的重要性。我们证明，需要对这四个元组进行像素列选择，以确保无错误的双色（二进制）线可视化。此外，我们将此模型表示为 M4 聚合，并讨论和评估它的一般线可视化，包括抗锯齿（非二进制）线可视化。

我们的方法与最先进的时间序列降维技术 [11] 显着不同，后者通常基于线简化算法 [25]，例如 Ramer-Douglas-Peucker [6, 14] 和 VisvalingamWhyatt算法[26]。这些算法的计算成本为 O(n log(n)) [19]，并且忽略了线到最终可视化的宽度 × 高度像素的投影。相比之下，我们的方法具有 O(n) 的复杂性并提供完美的可视化。

仅依靠关系运算符来减少数据，我们的可视化驱动的查询重写是通用的，可以应用于任何 RDBMS 系统。我们在 SAP HANA [10] 和 Postgres (postgres.org) 之上使用我们的算法的原型实现，展示了我们的技术在现实环境中的改进。

在本文的其余结构如下。在第 2 部分中，我们介绍我们的系统架构并描述我们的查询重写方法。在第 3 节中，我们将重点讨论折线图。此后，在第 4 节中，我们提供了面向可视化的数据聚合模型的详细信息，并讨论了所提出的 M4 聚合。在第 5 节中描述了现有时间序列降维技术的缺点之后，我们将我们的方法与这些技术进行了比较，并在第 6 节中评估了查询执行时间、数据效率和可视化质量方面的改进。在第 7 节中，我们讨论了其他相关工作，我们最终以第 8 节结束。

2. 查询重写

在本节中，我们将描述查询重写方法，以促进依赖关系数据源的可视化系统的数据缩减。

为了结合运算符进行数据缩减，需要重写对大容量时间序列数据源的原始查询。重写可以直接由可视化客户端完成，也可以通过关系数据库管理系统 (RDBMS) 的附加查询接口完成。无论重写查询的位置如何，实际的数据缩减始终由数据库本身计算。下图 2 说明了这种查询重写和以数据为中心的降维方法。

查询定义。查询的定义从可视化客户端开始，用户首先选择时间序列数据源、时间范围和可视化类型。数据源和时间范围通常定义原始查询的主要部分。我们的可视化客户端发出的大多数查询的形式都是 SELECT time , value FROM series WHERE time > t1 AND time < t2。但实际上，可视化客户端可以定义任意关系查询，只要结果是有效的时间序列关系即可。

时间序列数据模型。我们将时间序列视为具有两个数值属性的二元关系 T (t, v)：时间戳 t ∈ R 和值 v ∈ R。任何其他至少具有两个数值属性的关系都可以轻松投影到该模型。例如，给定关系 X(a, b, c)，并且知道 a 是数字时间戳，b 和 c 也是数值，我们可以通过投影和重命名导出两个独立的时间序列关系，即 Tb (t, v) = πt←a,v←b(X) 且 Tc(t, v) = πt←a,v←c(X)。

可视化参数。除了查询之外，可视化客户端还必须提供可视化参数宽度 w 和高度 h，即所需可视化的精确像素分辨率。确定确切的像素分辨率非常重要，我们将在第 6 节中介绍。对于大多数可视化，用户选择的图表大小 (wchart × hchart) 与用于显示的画布的实际分辨率 (w × h) 不同。几何图形的光栅化。图 3 使用折线图的示意性示例描述了这种差异，该折线图总共占用 14 × 11 屏幕像素，但仅使用 9 × 7 像素来绘制实际线条。当从这些可视化参数 w 和 h 导出数据缩减运算符时，我们的查询重写器做出以下假设。

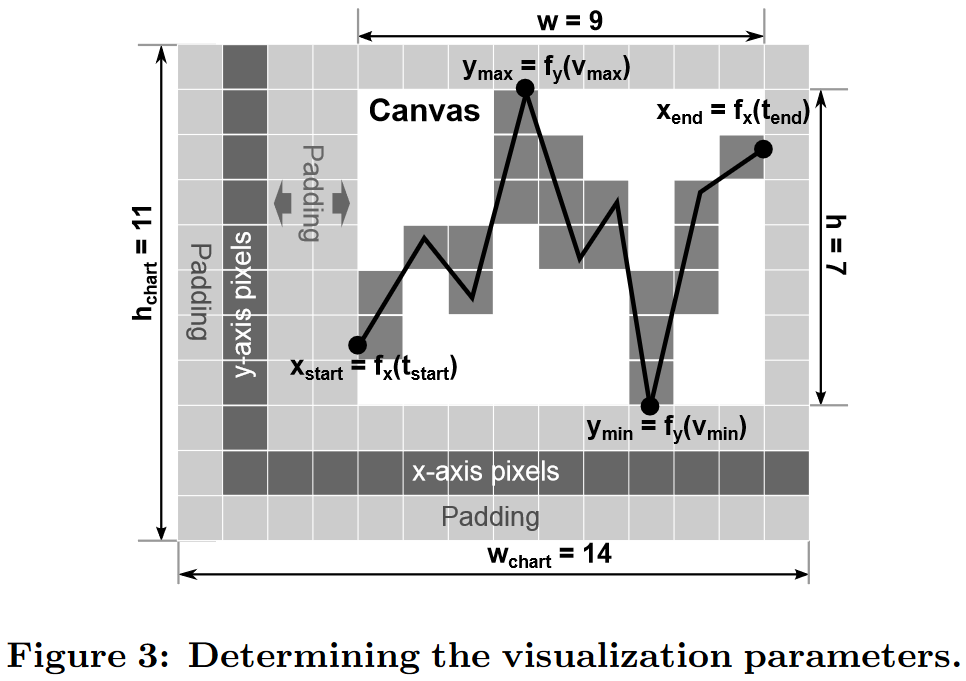
给定画布区域的宽度 w 和高度 h，可视化客户端使用以下几何变换函数 x = fx(t) 和 y = fy(v)，x, y ∈ R 将每个时间戳 t 和值 v 投影到可视化的坐标系。
f x ( t ) = w ⋅ ( t − t s t a r t ) / ( t e n d − t s t a r t ) f y ( v ) = h ⋅ ( v − v m i n ) / ( v m a x − v m i n ) ( 1 ) \begin{array}{l}f_x(t)=w\cdot(t-t_{start})/(t_{end}-t_{start})\\f_y(v)=h\cdot(v-v_{min})/(v_{max}-v_{min})\end{array}\quad(1) fx(t)=w⋅(t−tstart)/(tend−tstart)fy(v)=h⋅(v−vmin)/(vmax−vmin)(1)

然后，可视化客户端的绘图例程遍历投影的实值时间序列数据，以得出离散像素。我们假设所选时间序列的预计最小和最大时间戳以及值 (tstart、tend、vmin、vmax) 与实际值的左、右、下和上边界 (xstart、xend、ymin、ymax) 完全匹配画布区域，即，我们假设绘图例程不对数据应用额外的垂直或水平平移或重新缩放操作。在我们的评估中，在第 6 节中，我们将讨论这些假设的潜在问题。

查询重写。在我们的系统中，查询重写器处理所有与可视化相关的查询。因此，它接收查询 Q 和附加可视化参数宽度 w 和高度 h。重写的目标是对结果集大小超过特定限制的那些查询应用额外的数据缩减。重写过程的结果如图 4a 所示。一般来说，这样的重写查询QR包含以下子查询。

原始查询 Q，
对 Q 进行基数查询 QC，
基数检查（条件执行），
3a) 直接使用 Q 的结果，或
3b) 对 Q 执行额外的数据缩减 QD。

我们的系统将所有相关子查询组合成一个 SQL 查询，以确保快速查询执行。因此，我们首先利用数据库能够重用子查询的结果，其次假设计算原始查询选择的行数的执行时间与实际查询执行时间相比可以忽略不计。对于大多数现代数据库来说，这两个属性都是正确的，第一个属性有利于第二个属性。实际上，子查询重用可以通过公共表表达式 [23] 来实现，如 SQL 1999 标准所定义。

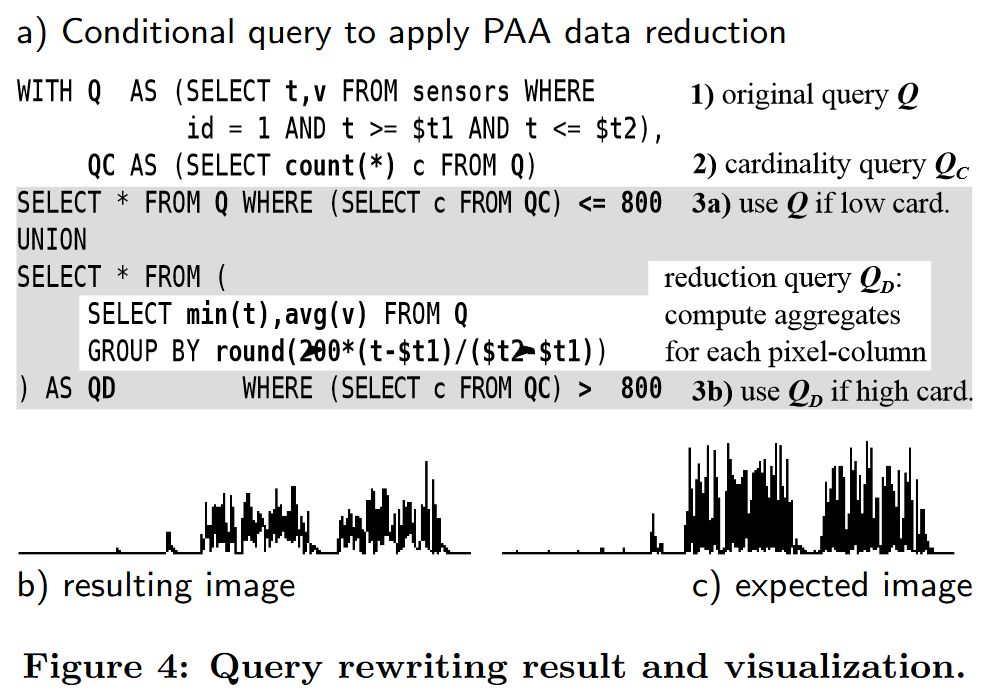
图 4a 中的 SQL 示例使用 w = 200 像素的宽度、4 · w = 800 个元组的基数限制，并且它使用简单的分段聚合近似 (PAA) [18]（一种简单的措施）来应用数据缩减用于时间序列降维。相应的可视化是折线图，我们只考虑宽度 w 来定义 PAA 参数。对于这种基于聚合的数据缩减运算符，我们将时间间隔与像素列对齐，以对查询级别的可视化过程进行建模。我们使用与可视化客户端使用的相同的几何变换 x = fx(t)，并将结果值舍入为 0 到 w = 200 之间的离散组键，即，我们使用以下分组函数。
f g ( t ) = r o u n d ( w ⋅ ( t − t s t a r t ) / ( t e n d − t s t a r t ) ) ( 2 ) f_g(t)=round(w\cdot(t-t_{start})/(t_{end}-t_{start}))\quad(2) fg(t)=round(w⋅(t−tstart)/(tend−tstart))(2)

图 4b 显示了可视化客户端从简化数据中得出的结果图像，图 4c 显示了从原始时间序列数据中得出的结果图像。平均聚合函数显着改变了时间序列的实际形状。在第 4 节中，我们将讨论不同类型的聚合函数在面向可视化的数据缩减方面的实用性。现在，让我们关注查询的整体结构。请注意，我们使用不同子查询 (3a) 和 (3b) 的并集对所描述的条件执行进行建模，这些子查询具有基于基数限制的矛盾谓词。这允许我们只执行一次查询 Q 的任何用户定义的查询逻辑。查询Q和数据缩减QD的执行全部由该单个查询涵盖，使得不需要将大量数据复制到额外的数据缩减或压缩组件。

3.时间序列可视化

在这项工作中，我们关注大量时间序列数据的折线图。下面关于时间序列可视化的简短题外话将解释我们的动机。

可视化时间序列数据的方法有很多种，但只有少数几种可以很好地处理大数据量。条形图、饼图和类似的简单图表类型每个显示元素占用太多空间 [8]。图 5 显示了足以满足大量数据的最常见图表。这些是折线图和散点图，其中仅使用几个像素即可呈现单个数据点。就空间效率而言，这两种简单的图表类型仅被空间填充方法超越[17]。然而，最普遍的可视化是折线图。存在于电子表格应用程序、数据分析工具、图表框架、系统监控应用程序等中。

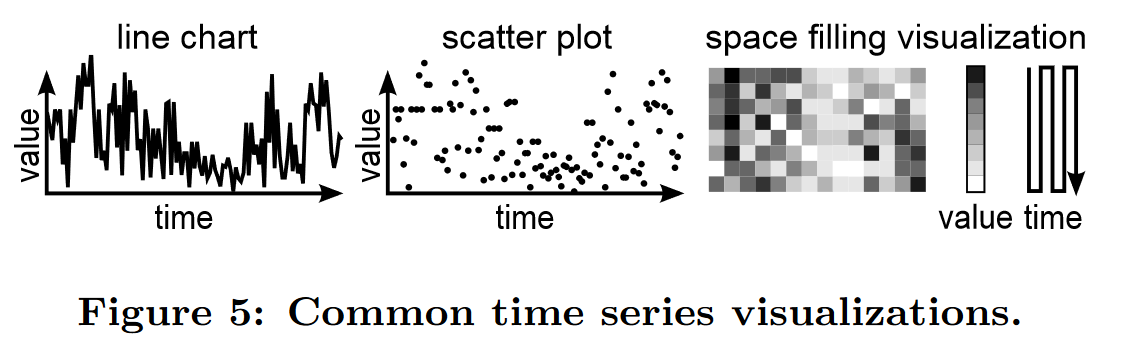
为了实现有效的数据缩减，我们需要考虑如何从底层数据创建可视化。对于散点图，此过程需要将时间序列关系 T (t, v) 与 t, v ∈ R 转换、缩放和舍入为离散像素 V (x, y) 与 x ∈ [1, w], y 的关系ε [1，h]。正如第 2 节中已经描述的，我们可以重用这种几何变换来减少数据。空间填充可视化是相似的。他们还将时间序列 T (t, v) 投影为离散值序列 V (i, l)，其中 i ∈ [1, w · h], l ∈ [0, 255]，其中 i 是序列，l 是要使用的亮度。

散点图的适当数据缩减是时间序列的二维分组，具有像素到组的一对一映射。因此，散点图（以及空间填充方法）需要从原始数据中选择最多 w·h 个元组才能生成正确的可视化效果。这可能会增加数十万个元组，特别是考虑到当今的高屏幕分辨率。相应的数据减少潜力是有限的。

对于大容量时间序列数据的折线图而言，情况并非如此。在 4.4 节中，我们将证明双色折线图所需元组的上限为 4·w 个。

4. 数据缩减运算符

我们的查询重写系统的目标是通过关系运算符（即使用数据聚合）在数据库中应用面向可视化的数据缩减。在文献中，我们没有找到任何描述数据聚合对栅格线可视化效果的全面讨论。大多数时间序列降维技术[11]都过于通用，并不是专门为线可视化而设计的。现在，我们将弥补这一缺点，并描述我们为减少数据而考虑和评估的几类运算符，并讨论它们对于线路可视化的实用性。

4.1 面向可视化的数据聚合

正如第 2 节中已经描述的，我们使用基于时间的分组对数据缩减进行建模，将时间间隔与可视化的像素列对齐。对于每个间隔以及每个像素列，我们可以使用以下选项之一计算聚合值。

正常聚合 。数据缩减的一种简单形式是使用聚合函数 min、max、avg、median、medoid 或 mode 来计算聚合值和聚合时间戳。使用（水平）分组函数 fg 和两个聚合函数 ft 和 fv 对时间序列关系 T (t, v) 进行数据缩减查询，可以在关系代数中定义：
f g ( t ) G f t ( t ) , f v ( v ) ( T ) ( 3 ) {f_g(t)}G{f_t(t),f_v(v)}(T)\quad(3) fg(t)Gft(t),fv(v)(T)(3)

我们已经在查询重写示例中使用了这种简单的聚合形式（图 4），选择最小（第一个）时间戳和平均值来建模分段聚合近似 (PAA) [18]。但任何平均函数，即使用 avg、median、medoid 或众数，都会显着扭曲时间序列的实际形状（见图 4b 与 4c）。为了保持时间序列的形状，我们需要关注每组的极值。例如，我们想要选择每组具有最小值 vmin 或最大值 vmax 的元组。不幸的是，关系代数的分组语义不允许选择非聚合值。

保值聚合 。为了根据计算出的聚合值选择相应的元组，我们需要再次将聚合数据与底层时间序列连接起来。因此，我们用基于时间的组键（fg 的结果）替换聚合函数之一，并将聚合结果与该组键和聚合值或时间戳上的 T 连接起来。特别是以下查询
π t , v ( T ⋈ f g ( t ) = k ∧ v = v g ( f g ( t ) G k ← f g ( t ) , v g ← f v ( v ) ( T ) ) ) ( 4 ) \pi_{t,v}(T\bowtie_{f_g(t)=k\wedge v=v_g}({f{g(t)}}G_{k\leftarrow f_g(t),v_g\leftarrow f_v(v)}(T)))\quad(4) πt,v(T⋈fg(t)=k∧v=vg(fg(t)Gk←fg(t),vg←fv(v)(T)))(4)

为每个聚合值选择对应的时间戳t vg = fv(v)，查询如下
π t , v ( T ⋈ f g ( t ) = k ∧ t = t g ( f g ( t ) G k ← f g ( t ) , t g ← f t ( t ) ( T ) ) ) ( 5 ) \pi_{t,v}(T\bowtie_{f_g(t)=k\wedge t=t_g}({f{g(t)}}G_{k\leftarrow f_g(t),t_g\leftarrow f_t(t)}(T)))\quad(5) πt,v(T⋈fg(t)=k∧t=tg(fg(t)Gk←fg(t),tg←ft(t)(T)))(5)

为每个聚合时间戳 tg = ft(t) 选择相应的值 v。请注意，如果每组存在重复值或时间戳，这些查询可能会为每组选择多个元组。然而，在我们的大多数大容量时间序列数据源中，时间戳是唯一的，并且值是具有多个小数位的实数值，因此平均重复次数不到总体数据的百分之一。在重复率较高的场景中，所描述的查询（4）和（5）需要使用额外的补偿聚合运算符来封装，以确保适当的数据缩减率。

采样。使用保值聚合，我们可以表达系统采样的简单形式，例如，使用以下查询选择每组的每个第一个元组。
π t , v ( T ⋈ f g ( t ) = k ∧ t = t m i n ( f g ( t ) G k ← f g ( t ) , t m i n ← m i n ( t ) ( T ) ) ) \pi_{t,v}(T\bowtie_{f_g(t)=k\wedge t=t_{min}}({f{g(t)}}G_{k\leftarrow f_g(t),t_{min}\leftarrow min(t)}(T))) πt,v(T⋈fg(t)=k∧t=tmin(fg(t)Gk←fg(t),tmin←min(t)(T)))

对于查询级别的随机采样，我们还可以将值保留聚合与 TABLESAMPLE 的 SQL 2003 概念或涉及 random() 函数的选择运算符结合起来。虽然这允许我们在数据库内进行数据采样，但我们将在评估中表明这些简单形式的采样不适合线条可视化。

复合聚合。除了所描述的每组生成单个聚合值的查询 (3)、(4) 和 (5) 之外，我们还考虑每组具有多个聚合值的复合查询。在关系代数中，我们可以将此类查询建模为使用相同分组函数的两个或多个聚合子查询的并集。或者，我们可以修改查询（4）和（5）以在再次加入基本关系之前选择每个组的多个聚合值或时间戳。然后，我们需要组合连接谓词，以便所有不同的聚合值或时间戳与其缺失的时间戳或缺失的值相关。以下 MinMax 聚合将提供复合聚合的示例。

最小最大聚合 。为了保持时间序列的形状，第一个直觉是按组选择垂直极值，我们将其表示为最小和最大元组。这是一个复合的保值聚合，如图 6a 中的 SQL 查询所示。该查询在将时间序列关系 Q 与聚合结果 QA 连接后，投影现有时间戳和值。 Q 由原始查询定义，如图 4a 所示。组键 k 基于 Q 到可视化坐标系的（水平）几何变换的舍入结果。如第 2 节中所述，重要的是，在将重新缩放的时间序列数据传递到线条绘制例程进行光栅化之前，此几何变换与可视化客户端执行的变换完全相同。最后，QA 与 Q 的连接基于组密钥 k 以及将 Q 中的值 v 与来自 QA 的 vmin 或 vmax 进行匹配。

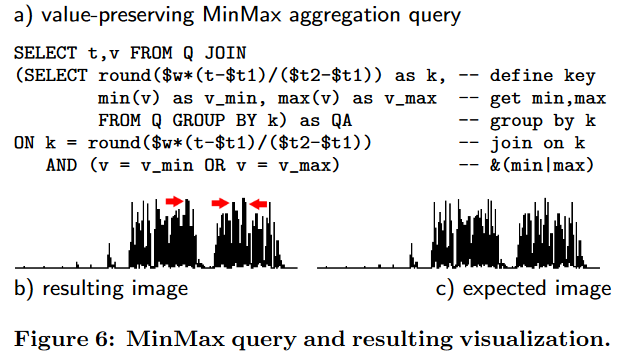
图 6b 显示了结果可视化，我们现在观察到它与原始数据 6c 的预期可视化非常匹配。在 4.3 节中，我们稍后讨论剩余的像素误差；如图6b中的箭头所示。

4.2 M4聚合

复合 MinMax 聚合关注每个像素列（即每个相应时间跨度）的垂直极值。出于数据缩减和数据分析的目的，已经存在选择极值的方法[12]。但他们中的大多数只部分考虑了数据可视化的影响，而忽略了数据到离散屏幕像素的最终投影。

基于缩减数据集的折线图将始终省略连接未选定元组的线，并且始终添加新的近似线以桥接两个连续选定元组之间的未选定元组。绘图例程的最终离散化过程显着减少了产生的错误（在实值可视化空间中）。这种效果是所提出的可视化驱动数据缩减的基本原理。

直观上，人们可能期望从恰好 w 个组中选择最小值和最大值，即元组 (tbottom, min(v)) 和 (ttop, max(v))，足以导出正确的线可视化。这种直觉是难以捉摸的，并且这种由 MinMax 聚合提供的数据缩减形式并不能保证时间序列的无错误线可视化。它忽略每个组中重要的第一个和最后一个元组。我们现在介绍 M4 聚合，它另外选择这些第一个和最后一个元组 (min(t), vfirst) 和 (max(t), vlast)。在 4.3 节中，我们将讨论 M4 如何超越 MinMax 直觉。

M4 聚合。 M4 是一个复合保值聚合（参见第 4.1 节），它将时间序列关系分组为 w 个等距时间跨度，使得每个组精确对应于可视化中的一个像素列。然后，对于每个组，M4 计算聚合 min(v)、max(v)、min(t) 和 max(t)------因此得名 M4------然后将聚合数据与原始时间序列连接起来，以添加缺少时间戳 tbottom 和 ttop 以及缺少值 vfirst 和 vlast。

在图 7a 中，我们展示了一个使用 M4 聚合的示例查询。此 SQL 查询与图 6a 中的 MinMax 查询非常相似，仅添加 min(t) 和 max(t) 聚合以及基于第一个和最后一个时间戳 tmin 和 tmax 的附加连接谓词。图 7b 描述了最终的可视化效果，它现在等于未简化的基础时间序列的可视化效果。在图 7a 中，我们展示了一个使用 M4 聚合的示例查询。此 SQL 查询与图 6a 中的 MinMax 查询非常相似，仅添加 min(t) 和 max(t) 聚合以及基于第一个和最后一个时间戳 tmin 和 tmax 的附加连接谓词。图 7b 描述了最终的可视化效果，它现在等于未简化的基础时间序列的可视化效果。

M4 的复杂性。对于基本关系 Q 的 n 个元组，所需的分组和聚合值的计算可以在 O(n) 中计算。聚合值与 Q 的后续等连接需要将 Q 中的 n 个元组与 4 · w 聚合元组，使用 O(n + 4 · w) 中的哈希连接，但 w 不依赖于 n 并且本质上受到物理显示分辨率的限制，例如，对于最新的 WHXGA 显示器，w = 5120 像素。因此，所描述的M4聚合的复杂度为O(n)。

4.3 聚合相关的像素错误

在图 8 中，我们比较了三种线可视化：a) 时间序列 Q 的示意图线可视化，b) M inM ax(Q) 的可视化，以及 c) M 4(Q) 的可视化。 M inM ax(Q) 不会选择每个像素列的第一个和最后一个元组，从而导致多种类型的线条绘制错误。

在图 8b 中，像素 (3,3) 未正确设置，因为相应行的开始元组和结束元组都不包含在缩减数据集中。这种缺失线错误 E1 在具有非常异构时间分布的时间序列中明显可见，即明显的间隙，导致像素列不保存任何数据（参见图 8b 中的像素列 3）。漏线错误通常会因额外的假线错误 E2 而加剧，因为线条绘制仍然需要连接两个元组来桥接空像素列。此外，这两种错误类型也可能发生在相邻像素列中，因为内列线并不总是代表列的完整像素集。额外的列间像素（位于内列像素下方或上方）可以从列间线导出。如果缩减的数据集不包含正确的列间线的正确元组，这将再次导致丢失或额外的像素。在图 8b 中，MinMax 聚合通过设置不需要的像素 (1,2) 来导致这样的错误 E3，该像素源自第一像素列中的最大元组和第二像素列中的（连续）最大元组之间的错误线。请注意，这些误差与所需光栅图像的分辨率无关，即与所选的组数无关。如果我们不显式选择第一个和最后一个元组，则无法保证包含用于绘制正确的列间线的所有元组。

4.4 M4 上限

根据对所描述的错误的观察，出现了问题：是否为每个像素列仅选择四个极值元组就能保证无错误的可视化。在下文中，我们证明了无错误的双色线可视化所需的元组上限的存在。

因此 viswh 首先使用线性变换函数 fx 和 fy 将 T 中的所有元组重新缩放到坐标系 R[1,w] × R[1,h]（参见第 2 节），然后测试所有离散像素和所有非离散像素离散线 -- 由转换后的时间序列的连续元组定义 -- 如果像素在线上或不在线上。为了简洁起见，我们省略了线光栅化的详细描述[2, 4]，并假设以下两个属性为真。

图 9 说明了定理 1 的推理。

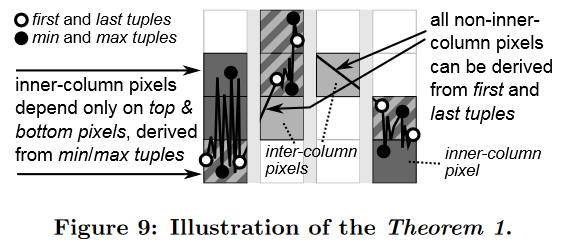
证明。假设可视化关系 V = viswh(T ) 表示任意时间序列 T 的双色线可视化的像素。假设元组只能属于由 G(T ) 定义且对应于像素列的组 B1 到 Bw 之一。那么只有一对连续的元组 pj ∈ Bi 和 pj+1 ∈ Bi+1，即每对连续的组 Bi 和 Bi+1 之间只有一条列间线。但是，由 T 中剩余的连续元组对定义的所有其他行必须定义内列行。

从引理 1 和 2 开始，所有内列像素都可以通过了解每列的顶部和底部内列像素来定义。此外，由于 fx 和 fy 是线性变换，因此我们可以从每个组 Bi 的最小和最大元组 (tbottomi , vmini ), (ttopi , vmaxi ) 导出每列的顶部和底部像素。剩余的列间像素可以从所有列间线导出。由于每对连续组 Bi 和 Bi+1 之间只有一条列间线 pjpj+1，因此元组 pj ∈ Bi 是 Bi 的最后一个元组 (tmaxi vlasti )，pj+1 ∈ Bi+1 是第一个元组Bi+1 的元组 (tmini+1 , vfirsti+1 )。

因此，可视化关系 V 的所有像素都可以从每个组 Bi 的元组 (tbottomi , vmini ), (ttopi , vmaxi ), (tmaxi vlasti ), (tmini , vfirsti ) 中导出，即 V = viswh(GM4( T )) = viswh(T )。

利用定理1，我们还可以推导出

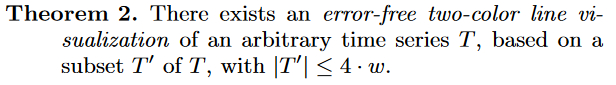
无论 T 有多大，从 T 中选择正确的 4·w 元组都可以让我们创建 T 的完美可视化。显然，为了线可视化的目的，M4 查询提供了数据高效、可预测的数据缩减。

5. 时间序列数据缩减

在第 4 节中，我们讨论了作为数据缩减措施的平均、系统抽样和随机抽样。它们通常为时间序列降维提供了一些实用程序，并且还可以为某些类型的可视化提供有用的数据缩减。然而，对于光栅化线可视化，我们现在已经证明了选择正确的最小、最大、第一个和最后一个元组的必要性。因此，如果不能确保包含这些重要的元组，任何平均、系统或随机方法都将无法获得线可视化的良好结果。

与我们的方法相比，最有竞争力的方法（如文献[11]中所示）是基于线简化的时间序列降维技术。例如，Fu 等人。基于感知重要点（PIP）减少时间序列[12]。此类方法通常应用在线的每三个连续点之间定义的距离测量，并尝试针对选定的数据缩减率最小化该测量。此 min - 问题由 min-# 问题补充，其中需要找到定义距离的最小点数。然而，由于该优化问题的最坏情况复杂度为 O(n2) [19]，因此有许多用于线简化的启发式算法。最快的一类算法在 O(n) 内按顺序工作，仅处理直线上的每个点一次。其他两个主要类的复杂度为 O(n log(n))，并且要么合并点，直到满足某个误差标准（自下而上），要么分割线（自上而下），从由第一个定义的初始近似线开始以及原始线的最后一点。后一种方法通常提供对原始线更好的近似[25]。我们基于聚合的数据缩减（包括 M4）的复杂度为 O(n)。

近似质量。为了确定派生时间序列的近似质量，大多数时间序列降维技术使用几何距离度量，在近似线段和原始线的（删除的）点之间定义。

最常见的度量是欧几里得（垂直）距离，如图 10a) 所示，它是点 pk 到线段 pipj 的最短距离。其他常用的距离度量是三角形的面积 (pi, pk, pj)（图 10b）或 pk 到 pipj 的垂直距离（图 10c）。

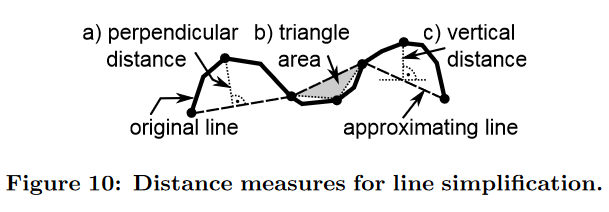
然而，当使用离散像素可视化一条线时，所描述的测量的主要缺点是它们的通用性。它们是几何度量，以 R × R 定义，并且不考虑离散 2D 空间中的不连续性，如两个相邻像素行或两个相邻像素列的切割线所定义的。对于我们的方法，我们参考实际的可视化来确定数据缩减算子的近似质量。

可视化质量。相同尺寸的两个图像可以轻松地逐像素进行比较。一个简单、常用的误差测量是均方误差 MSE =1 wh Σw x=1 Σh y=1(Ix,y(V1) − Ix,y(V2))2，其中 Ix,y 定义亮度值可视化 V 的像素 (x, y)。尽管如此，王等人。已经表明[27]基于MSE的测量，包括常用的峰值信噪比（PSNR）[5]，并不能很好地近似人类感知模型，并开发了结构相似性指数（SSIM）。为了简洁起见，并且由于该措施的复杂性，我们不得不继续下去，而不对该措施进行详细描述。 SSIM 产生 1 到 -1 之间的相似度值。两个可视化 V1 和 V2 之间的相关归一化距离度量定义为：

D S S I M ( V 1 , V 2 ) = 1 − S S I M ( V 1 , V 2 ) 2 DSSIM(V_1,V_2)=\frac{1-SSIM(V_1,V_2)}2 DSSIM(V1,V2)=21−SSIM(V1,V2)

我们使用 DSSIM 来评估基于缩减时间序列数据集的线可视化的质量，并将其与底层未缩减时间序列数据集的原始线可视化进行比较。

6. 评估

在下面的评估中，我们将比较 M4 聚合的数据缩减效率与最先进的行简化方法以及常用的朴素方法（例如平均、采样和舍入）。因此，我们将所有考虑的技术应用于几个现实世界的数据集，并测量所得的可视化质量。对于所有可以使用关系代数表示的基于聚合的数据缩减运算符，我们还评估查询执行性能。

6.1 真实世界时间序列数据

我们考虑三个不同的数据集：法兰克福证券交易所 6 周内单一股票的价格（700k 元组）、足球速度传感器 71 分钟的价格 [22]（球号 8，700 万行）以及一个来自半导体制造机器的电力传感器的一周传感器数据[15]（传感器 MF03，55M 行）。在图 11 中，我们显示了这些数据集的摘录，以显示时间和价值分布的差异。

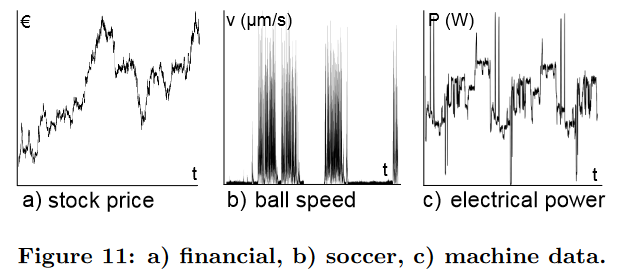
例如，金融数据集 (a) 每个工作日包含超过 20000 个元组，且股价随时间变化缓慢。与此相反，足球数据集 (b) 每秒包含超过 1500 个读数，最好将其描述为突发序列。最后，100Hz 的机器传感器数据 © 构成了具有低、高和突发变化的时间跨度的混合信号。

6.2 查询执行性能

在第 4 节中，我们描述了如何使用关系代数来表达简单采样或基于聚合的数据缩减运算符，包括我们提出的 M4 聚合。我们现在评估这些不同运算符的查询执行性能。所有评估的查询均以 SQL 查询的形式通过 ODBC 通过 (100Mbit) 广域网发送到虚拟化共享 SAP HANA v1.00.70 实例，该实例在远程位置的 SAP 数据中心中运行。

所考虑的查询是：1）选择要可视化的所有元组的基线查询，2）计算最多 4·w 个平均元组的 PAA 查询，3）选择最多 w·h 舍入的二维舍入查询元组，4) 选择 4·w 个随机元组的分层随机抽样查询，5) 选择 4·w 个第一个元组的系统抽样查询，6) 从 2·w 个组中选择两个最小和最大元组的 MinMax 查询，最后 7) 我们的 M4 查询从 w 组中选择所有四个极值。请注意，我们调整了组数，以确保在相似的数据缩减率下进行公平比较，以便任何缩减查询最多可以生成 4·w 个元组。所有查询均使用宽度 w = 1000 和高度 h = 200（如果需要）进行参数化。

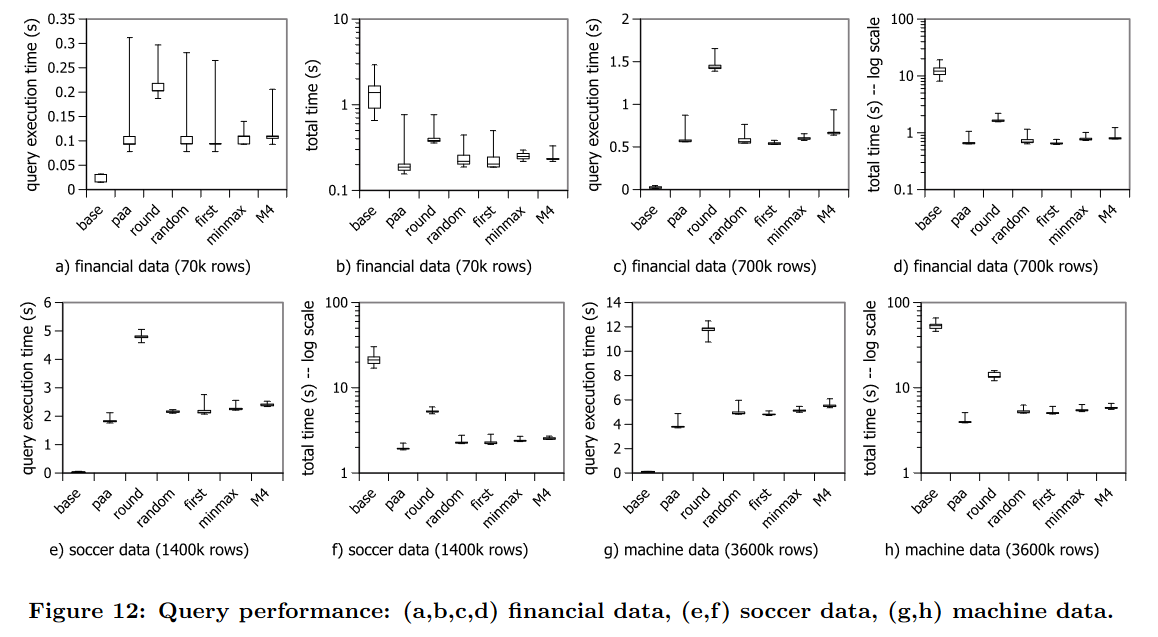
在图 12 中，我们绘制了三个数据集相应的查询执行时间和总时间。总时间衡量从发出查询到在 SQL 客户端接收所有结果的时间。对于金融数据集，我们首先从数据中选择了三天（70k 行）。我们运行每个查询 20 次并获得查询执行时间，如图 12a 所示。最快的查询是基线查询，因为它是一个简单的选择，无需额外的运算符。其他查询速度较慢，因为它们必须计算额外的数据缩减。最慢的查询是舍入查询，因为它按 w 和 h 对二维数据进行分组。其他数据缩减查询仅需要一个水平分组。将这些执行时间与图 12b 中的总时间进行比较，我们发现基线查询在查询执行中失去了优势，最终比其他查询慢了一个数量级。即使对于 70k 行的少量数据，基线查询也主要由额外的数据传输时间决定。就最终的总时间而言，所有数据缩减查询都处于同一水平，并设法保持在一秒以下。请注意，M4 聚合的查询执行时间和总时间并没有明显高于其他查询。从财务数据集中选择 700k 行（30 天）时，观察结果相似（图 12c 和 12d）。基于聚合的查询（包括 M4）总体上比基线快一个数量级，而查询执行时间的增加可以忽略不计。

在足球和机器数据集上运行不同类型的数据缩减查询时，我们的测量结果显示非常相似的结果。我们从足球数据集中请求 1400k 行，从机器数据集中请求 3600k 行。图 12(e-h) 中的结果再次显示总时间提高了一个数量级。

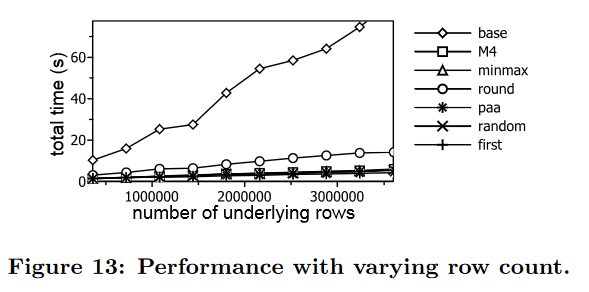
我们重复了所有测试，使用在 Red Hat 6.3 上运行的 Xeon E5-2620（配备 2.00GHz、64GB RAM、1TB HDD（无 SSD））上运行的 Postgres 8.4.11 RDBMS，与 HANA 实例托管在同一数据中心。所有数据均由 RAM 磁盘提供。 Postgres 工作内存设置为 8GB。在图 13 中，我们显示了足球数据集的示例性结果，绘制了增加的请求时间跨度（即增加的基础行数）的总时间。我们再次观察基线查询在很大程度上取决于有限的网络带宽。基于聚合的方法再次表现得更好。我们对财务数据集和机器数据集进行了可比较的观察。

Postgres 和 HANA 系统的结果表明，获取所有行的基线查询主要取决于数据库传出网络带宽。相比之下，对于任何数量的底层数据，所有基于聚合的查询的结果集大小或多或少是恒定的，并且低于 4·w。它们的总时间主要取决于数据库内部查询的执行时间。该评估还表明，我们提出的 M4 聚合与常见的基于聚合的数据缩减技术同样快。在我们的所有场景中，M4 可以将用户等待数据的时间减少一个数量级，并且仍然提供正确的元组以实现高质量的线条可视化。

6.3 可视化质量和数据效率

我们现在评估有关可实现的可视化质量的稳健性和数据效率。因此，我们使用不同数量的水平组 nh 来测试 M4 和其他聚合技术。我们从 nh = 1 开始，到 nh = 2.5 · w 结束。因此，我们希望选择最多 10·w 行，即无错误双色线可视化实际所需数据的两倍。基于简化的数据集，我们计算（近似）可视化并将其与原始数据集的（基线）可视化进行比较。所有考虑的可视化都是使用开源 Cairo 图形库 (cairgraphics.org) 绘制的。距离度量是 DSSIM，如第 5 节中所述。评估场景的基础原始时间序列是来自财务数据集的 70k 元组（3 天）。相关可视化的 w = 200 和 h = 50。在评估场景中，我们允许组数 nh 与可视化的宽度 w 不同。这将显示我们方法的稳健性。然而，在实际实施中，工程师必须确保 nh = w 才能达到最佳效果。除了基于聚合的运算符之外，我们还将我们的方法与三种不同的线路简化方法进行比较，如第 5 节中所述。我们使用 Reumann-Wikham 算法 (reuwi) [24] 作为顺序线路简化的代表，即自上而下的 Ramer -Douglas-Peucker (RDP) 算法 [6, 14] 和自下而上的 Visvalingam-Whyatts (visval) 算法 [26]。 RDP 算法不允许设置所需的数据缩减比率，因此我们预先计算了会产生与所考虑的 nh 成比例的元组数量的最小值。

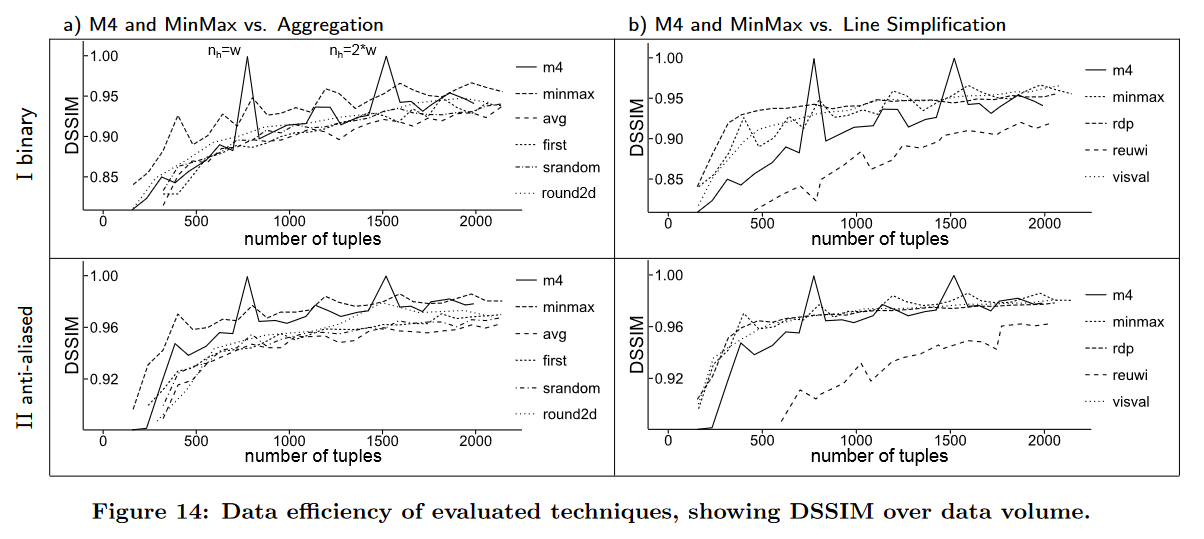
在图 14 中，我们绘制了所测量的结果可视化质量 (DSSIM) 与所应用的数据缩减技术的每个不同分组 nh = 1 到 nh = 2.5 · w 的结果元组数量的关系。为了便于阅读，我们截去了所有 DSSIM < 0.8 的低质量结果。元组数量越少，DSSIM 越高，用于线可视化的相应技术的数据效率就越高。图 14aI 和 14bI 描绘了二进制线可视化的这些测量，图 14aII 和 14bII 描绘了抗锯齿线可视化的这些测量。我们现在观察到以下结果。

采样和平均运算符（avg、first 和 srandom）为每个（水平）组选择一个聚合值。它们都显示相似的结果并提供最低的 DSSIM。正如第 4 节中所讨论的，他们通常无法选择对线光栅化很重要的元组，即设置正确的内列和列间像素所需的最小、最大、第一个和最后一个元组。

2D 舍入 需要额外的垂直分组为 nv 组。我们设置 nv = w/h · nh 为具有比例垂直分组。 2Drounding 的平均可视化质量高于平均和采样。

MinMax 查询选择 min(v) 和 max(v) 以及每组相应的时间戳。它们可以在低数据量的情况下提供非常高的 DSSIM 值。平均而言，它们比所有基于聚合的技术（包括 M4，见图 14a）具有更高的数据效率，但部分被线路简化方法超越（见图 14b）。

线路简化 平均而言，技术（RDP 和 visval ）比基于聚合的技术提供更好的结果（比较图 14a 和 14b）。如前所述 [25]，自上而下 (RDP) 和自下而上 (visval) 算法的性能比顺序算法 (reuwi) 好得多。然而，在光栅化线可视化的背景下，它们在 nh = w 和 nh = 2 · w 时被 M4 和 MinMax 超越。这些技术经常会错过最小、最大、第一个或最后一个元组中的一个，因为这些元组不一定符合用于线简化的几何距离度量，如第 5 节中所述。

M4 查询选择 min(v)、max(v)、min(t)、max(t) 以及每组相应的时间戳和值。平均而言，M4 提供 DSSIM > 0.9 的可视化质量，但通常低于 MinMax 和线路简化技术。然而，在 nh = w 时，即在 w 的任何因子 k 时，M4 提供完美（无错误）的可视化。任何 nh = k · w 和 k ∈ N+ 的分组还包括 nh = w 的最小、最大、第一个和最后一个元组。

抗锯齿。 二进制可视化（图 14I）和抗锯齿可视化（图 14II）的观察结果非常相似。抗锯齿可视化的绝对 DSSIM 值甚至比二进制可视化更好。这是由二进制可视化中的单个像素错误引起的，意味着从一个极端到另一个极端的全颜色交换，例如从背面 (0) 到白色 (255)。抗锯齿可视化中的像素错误不太明显，尤其是在过度绘制的区域中，这对于大容量时间序列数据来说很常见。例如，缺失的线通常会导致亮度的小幅增加，而不是全颜色值的完全交换，并且额外的假线将导致像素的亮度小幅下降。

6.4 像素误差评估

图 15 显示了应用于机器数据集 400 秒（40k 元组）的 M4、MinMax、RDP 和平均 (PAA) 的视觉结果。我们对每个可视化仅使用 100×20 像素来揭示像素每个操作员的错误。因此，M4 也呈现出无误差的基线图像。我们标记了 MinMax、RDP 和 PAA 的像素错误；黑色代表与基础图像相比额外的像素，白色代表缺失的像素。

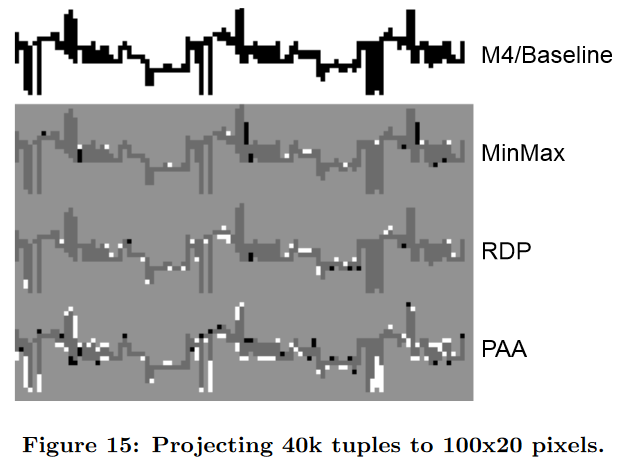
我们看到 MinMax 如何绘制非常长的错误连接线（图表中三个主要正峰值的右侧）。 MinMax 也有几个较小的误差，都是由相同的效应引起的。在这方面，RDP 更好，因为未选择的点到一条很长的假连接线的距离也非常高，RDP 将不得不再次分割这条线。 RDP 还在时间序列方差较低的区域应用轻微平均，因为低变化值之间的距离较小也会减少相应的测量距离。大多数像素错误是由基于 PAA 的数据缩减产生的，主要是由垂直极值的平均引起的。总体而言，MinMax 产生 30 个错误像素，RDP 产生 39 个错误像素，PAA 产生超过 100 个错误像素。 M4 保持无错误。

6.5 数据减少潜力

现在让我们回到第 1 节中的激励示例。对于所描述的场景，我们预计有 100 个用户尝试直观地分析以 100Hz 记录的 12 小时的传感器数据。每个用户必须等待超过 400 万行数据，直到他或她可以目视检查传感器信号。假设使用依赖于基于 M4 的聚合的折线图来可视化传感器数据，并且图表的最大宽度为 w = 2000 像素。那么我们知道 M4 最多会从时间序列中选择 4·w = 8000 个元组，与选择的时间跨度无关。为所有 100 个用户提供无错误折线图所需的最大元组数量为 100 个用户·8000 = 800000 个元组；而不是之前的 4.63 亿元组。因此，在这种情况下，我们实现了超过 1:500 的数据缩减率。

7. 相关工作

在本节中，我们讨论现有的可视化系统，并概述相关的数据缩减技术，讨论与我们的方法的差异。

7.1 可视化系统

关于可视化相关的数据缩减，当前最先进的可视化系统和工具分为三类。它们 (A) 不使用任何数据缩减，或 (B) 计算并将图像而不是数据发送到可视化客户端，或 © 依赖于数据库外部的额外数据缩减。在图 16 中，我们将这些系统与我们的解决方案 (D) 进行比较，显示每种类型的系统如何应用和减少时间序列关系 T 上的关系查询 Q。请注意，细箭头表示低容量数据流，粗箭头表示原始数据需要在系统组件之间传输或传输到客户端。

**可视化分析工具。**许多可视化分析工具都是 A 类系统，不应用任何与可视化相关的数据缩减，尽管它们通常包含可用于此目的的最先进的（关系）数据引擎 [28]。为了满足我们的可视化需求，我们已经评估了此类工具的四种常见候选工具：Tableau Desktop 8.1 (tableausoftware.com)、SAP Lumira 1.13 (saplumira.com)、QlikView 11.20 (clickview.com) 和 Datawatch Desktop 12.2 (datawatch.com) 。但这些工具都无法快速轻松地可视化具有 100 万行或更多行的大量时间序列数据。由于所有工具都允许处理数据库中的数据或提供工具内部数据引擎，因此我们看到了在此类系统中实施我们的方法的绝佳机会。为简洁起见，我们无法对这些工具进行更详细的评估。

客户端-服务器系统。第二种系统类型 B 通常用于基于网络的解决方案，例如雅虎财经 (finance.yahoo.com) 或 Google 财经 (google.com/finance) 等财经网站。这些系统通过生成和缓存光栅图像并发送这些图像而不是大多数较小可视化的实际数据来减少数据量。纯粹基于图像的系统通常提供较差的交互性，并且由 C 型补充系统支持，该系统作为富客户端应用程序实现，允许交互式地探索数据。系统B和C通常依赖于数据引擎和客户端之间的附加数据缩减或图像生成组件。假设系统 C 允许任意非聚合用户查询 Q，他们将定期需要将大型查询结果从数据库传输到外部数据缩减组件。这可能会消耗大量的系统内部带宽并严重影响整体性能，因为数据传输是成本最高的操作之一。

以数据为中心的系统。我们的可视化系统（D 型）可以直接在数据引擎内运行昂贵的数据缩减操作，并且仍然实现与富客户端可视化系统（C 型）提供的相同级别的交互性。我们的系统使用额外的数据缩减运算符重写原始查询 Q，生成新的查询 QR。当执行新查询时，数据引擎可以联合优化单个查询图中的所有运算符，并且最终（物理）运算符都可以直接访问共享的内存中数据，而不需要额外的、昂贵的数据传输。

7.2 数据缩减

下面我们概述了常见的数据缩减方法以及它们与可视化的关系。

量化。许多可视化系统显式或隐式地将连续时间序列数据减少为离散值，例如通过生成图像，或简单地通过四舍五入数据，例如仅保留两位小数。舍入函数是一种满射函数，不允许正确再现原始数据。在我们的系统中，我们还考虑有损、基于舍入的缩减，甚至可以将其建模为关系查询，从而促进以数据为中心的计算。

时间序列表示。关于时间序列表示的工作有很多[9]，特别是数据挖掘任务[11]。与我们的目标类似，大多数方法的目标是获得完整时间序列的更小的表示。在许多情况下，这是通过将时间序列（水平）分割为等距或基于分布的时间间隔并计算每个间隔的聚合值（平均值）来实现的[18]。然后，通过将聚合映射到有限的字母表（例如，基于值的（垂直）分布）来进一步减少。结果是，例如，近似原始时间序列的字符序列或线段列表（参见第 5 节）。然后通过在数据挖掘任务中使用它来测试表示的有效性，例如时间序列相似性匹配[29]。我们的方法的主要区别在于我们关注关系运算符并结合可视化的语义。现有的方法都没有讨论线栅格化的相关方面，从而促进我们方法的高质量和数据效率。

离线聚合和概要。传统上，OLAP 多维数据集中的时态业务数据的聚合粒度非常粗。聚合级别的数量受到限制，例如年、月和日，并且聚合函数也受到限制，例如计数、平均值、总和、最小值和最大值。出于可视化的目的，这种预先聚合的数据可能不能很好地表示原始数据，特别是在考虑时间分辨率为几毫秒的大量时间序列数据时。通过提供（分层或遗忘）数据概要可以部分缓解该问题 [7, 13]。然而，概要技术再次依赖于常见的时间序列降维技术[11]，因此容易出现近似误差。在这方面，我们看到了面向可视化的数据概要系统的开发，该系统使用所提出的 M4 聚合来提供无错误的可视化，这是未来工作的一个具有挑战性的主题。

在线聚合和流媒体。尽管本文重点关注静态数据的聚合，但我们的工作最初是由高速流数据的交互式、实时可视化的需求驱动的[16]。事实上，我们可以将 M4 聚合应用于在线聚合，即在 O(n) 中并在输入流上的单次传递中导出四个极值元组。自定义 M4 实现可以扫描输入数据中的极值元组而不是极值，从而避免后续连接，如关系 M4 所要求的（参见第 4.2 节）。

数据压缩。我们目前只考虑应用层面的数据缩减。任何额外的传输层数据缩减技术，例如数据包压缩或数值数据的专门压缩 [20, 11]，都是对我们的数据缩减的补充。

内容改编。我们的方法类似于一般的内容适应[21]，广泛用于基于网络的系统中的图像、视频和文本。内容适应是我们向关系方法扩展的基本思想之一，特别关注线条可视化的语义。

统计方法。统计数据库[1]可以提供近似结果。它们为用户查询提供高度简化的近似答案。然而，这些答案不能很好地代表用于线可视化目的的原始数据，因为它们应用了简单的随机或系统抽样，如第 4 节中所讨论的。理论上，统计数据库可以用我们的方法进行扩展，以服务于例如 M4或 MinMax 查询结果作为近似答案。

7.3 可视化驱动的数据缩减

Burtini 等人已经部分描述了使用可视化参数来减少数据。 [3]，他们使用可视化的宽度和高度来定义某些时间序列压缩技术的参数。然而，他们描述了 C 型客户端-服务器系统（参见图 16），在数据库外部应用数据缩减。在我们的系统中，我们通过查询重写的方式将所有数据处理下放到数据库中。此外，他们使用 w 组的平均聚合，即仅 1·w 个元组，作为基线，并且不考虑原始时间序列的可视化。因此，它们过度简化了实际问题，并且生成的折线图将丢失垂直极值的重要细节。他们没有适当地讨论光栅化线可视化的语义。

8 结论

在本文中，我们介绍了一种可视化驱动的查询重写技术，该技术有助于以数据为中心的时间序列降维。我们展示了如何将所有与可视化相关的查询封装到附加数据缩减运算符中的 RDBMS。特别是，我们考虑了基于聚合的数据缩减技术，并描述了它们如何与建议的查询重写集成。

我们的方法专注于折线图，作为时间序列可视化的主要形式，利用线栅格化的语义来驱动大容量时间序列数据的数据缩减。我们引入了新颖的 M4 聚合，它从与折线图像素列相对应的时间跨度中选择最小、最大、第一个和最后一个元组。使用 M4，我们能够将数据量减少两个数量级，将延迟减少一个数量级，同时确保像素完美的线条可视化。

未来，我们希望将当前对线条可视化的关注扩展到其他形式的可视化，例如条形图、散点图和空间填充可视化。我们的目标是提供一个考虑可视化渲染语义的数据缩减通用框架。我们希望这篇深入的、跨学科的数据库和计算机图形研究论文能够激励其他研究人员调查这两个领域之间的界限。