欢迎收藏Star我的Machine Learning Blog:https://github.com/purepisces/Wenqing-Machine_Learning_Blog。如果收藏star, 有问题可以随时与我交流, 谢谢大家!
预测系统的分类指标(精确率、召回率和 F1 值)
简介
让我们来谈谈预测系统的分类指标以及对精确率、召回率和F1分数的直观解释。每当我们设计预测系统时,无论是统计模型还是复杂的神经网络,我们都希望看到它的表现如何。我们希望准确了解输出的质量,不仅如此,我们还希望能够将它们与其他当代或最先进的系统进行比较,以证明我们的方法更优。
制定这样的比较并不简单。我们必须从多个角度提出质量问题,这需要一个良好的指标来量化输出的质量,使它们能够直接与其他方法进行比较,并确保输入不变性。对于输入不变性,这意味着处理特定类型数据的数据集或模型不应在任何其他类型的问题上具有偏见的优势。
输入不变性意味着无论模型处理的数据类型或问题是什么,指标都应公平地评估性能。

基本定义
在开始讨论指标之前,我们必须先了解一些基本的类别定义,我们可以将输出分组到这些类别中。
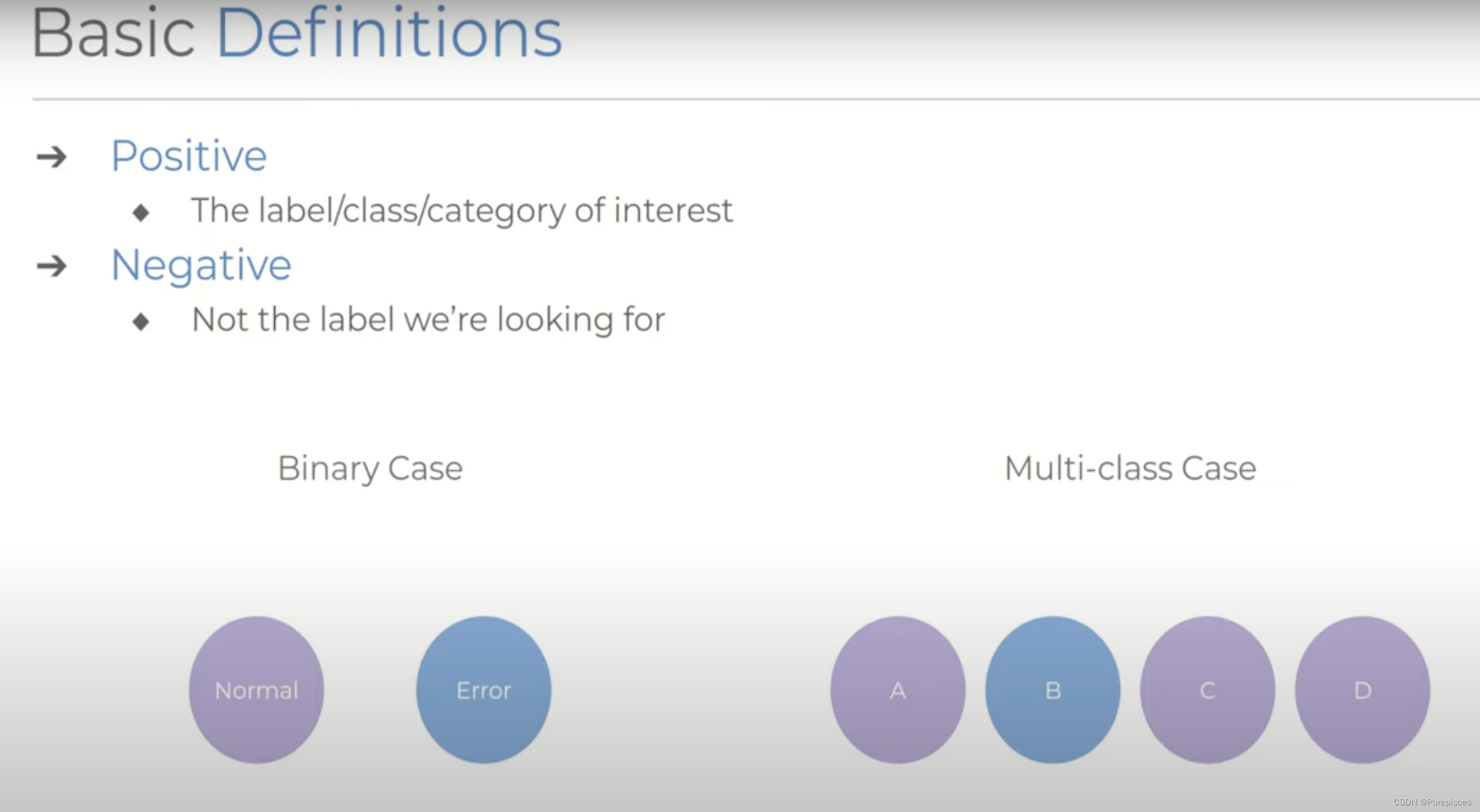
假设我们有一个系统,它对对象的类别进行预测,我们称 正例 为我们感兴趣的标签或类别。
- 例1:检测数据集中的错误。如果我们感兴趣的是测量识别错误情况的性能,我们会将其归类为正例,正常操作为负例。
- 例2:将项目分类为a、b、c和d四种不同类别。如果我们想测量与类别b有关的性能,那么在这种情况下,b是正例,其他任何(a、c和d)都是负例。
关键点在于,我们所有的指标都是针对我们选择定义为正例的类别。随着我们探索不同的指标,这一区别变得重要和明显,特别是对于多类别系统。
正例非常关键,因为我们将讨论的所有指标都是针对我们选择定义为正例的类别。这意味着我们计算的性能度量将取决于我们认为的正例是什么。
在多类别系统中(即有两个以上的类别),定义正例变得尤为重要和明显。每个类别都可以单独作为正例进行评估,这会影响最终的指标。
预测类别
基于这些定义,我们可以将对某些数据所做的预测进一步划分为四个有用的组:
- 真正例(TP):当标签为正且我们预测为正时。
- 假正例(FP):当标签为负且我们预测为正时。
- 真负例(TN):当标签为负且我们预测为负时。
- 假负例(FN):当标签为正且我们预测为负时。
这些值通常表示为每个类别中的预测数量或相对于所有预测的百分比。
真正例、假正例、真负例和假负例的数量可以表示为原始数字或作为系统所做总预测数的百分比。

准确率
我们将从最基本的指标开始,并正式定义什么是准确率。几乎每个人都应该对这一概念有近乎本能的理解。为了测量我们系统的准确率,我们计算正确答案的数量,并将其表示为我们给出的所有答案的一部分。更正式地,通过我们之前的定义,我们的系统的准确率是由整个预测集中的真正例和真负例的数量给出的。
Accuracy = Total Correct Guesses Total Guesses = T P + T N T P + T N + F P + F N \text{Accuracy} = \frac{\text{Total Correct Guesses}}{\text{Total Guesses}} = \frac{TP + TN}{TP + TN + FP + FN} Accuracy=Total GuessesTotal Correct Guesses=TP+TN+FP+FNTP+TN
准确率基本上告诉我们在所有的猜测中我们有多少答案是正确的,值得注意的是,这没有考虑猜测是关于正标签还是负标签。但是在测量性能时,单纯的准确率有一个明显的问题,这在处理偏差数据集时变得明显。
偏差示例
假设我们有一个数据集,其中几乎所有的标签都是负的,只有百分之一是正的。如果模型决定只输出负预测,并且不做任何正预测,它仍然会被计算为有99%的准确率。这不仅仅是一个玩具示例。在疾病检测或预测系统故障等场景中,正常情况通常会大大超过任何异常情况。即使是具有较轻偏差的数据集,其性能指标也可能以这种方式被扭曲,只是稍微更微妙一些。
指标偏差
偏差:偏差是指模型性能指标的扭曲或失真。这可能发生在指标未能准确反映模型的真实性能时,通常是由于数据集不平衡。
微妙偏差:在具有较轻不平衡的数据集中(正负案例的分布不是极端偏差但仍不平衡),准确率指标的扭曲可能不会立即显现出来。这种微妙的偏差意味着准确率指标仍然可能给出一个错误的乐观视图。
轻度不平衡数据集
在轻度不平衡的数据集中,像准确率这样的性能指标的扭曲不像在高度不平衡的情况下那样明显,因为准确率仍然相对较高,但不平衡不足以使扭曲显而易见。
为什么它不那么明显
- 相对较高的准确率:在轻度不平衡的数据集中,80%的准确率不会立即显示出问题,因为它看起来相当不错。
- 不太极端的不平衡:不平衡程度较轻,因此准确率指标看起来不像在高度不平衡的情况下那样具有误导性高。
- 隐藏的糟糕表现:模型未能识别正例被更多的正确识别的负例所掩盖,使得准确率的扭曲在乍一看不那么明显。

精确率
这时精确率这样的指标就派上用场了。精确率是衡量你对我们感兴趣的标签,即正例的猜测有多准确。我们通过将正确的正例猜测数量除以所有的正例猜测数量来计算它。正式地,是真正例的数量除以真正例加假正例的数量。
Precision = Correct Positive Guesses Total Positive Guesses = T P T P + F P \text{Precision} = \frac{\text{Correct Positive Guesses}}{\text{Total Positive Guesses}} = \frac{TP}{TP + FP} Precision=Total Positive GuessesCorrect Positive Guesses=TP+FPTP
优化这个指标的系统的目标是尽可能少地在猜测正标签时犯错误。回到一个系统只会猜测所有东西都是负例的例子,我们会看到精确率评分会惩罚模型,因为它未能猜测任何正标签,因此得分为零。
精确率的局限性
精确率仍然不能完全反映全貌,因为它不考虑任何负标签。一个模型可以通过非常少的正预测并在这些少数情况下是正确的来获得高精确率。例如,如果它只做一个正预测,并且该预测是正确的:
Precision = 1 1 = 1 或 100 percent \text{Precision} = \frac{1}{1} = 1 \text{ 或 } 100 \ \text{percent} Precision=11=1 或 100 percent
这个高精确率分数是误导性的,因为模型可能没有做足够的正预测,以在现实世界的场景中变得有用。

召回率
现在我们有了召回率,它类似于精确率的对应指标。不同的是它将负标签纳入了方程。它询问你在所有存在的正标签中找到了多少正标签,几乎直接解决了精确率的问题。这个方程归结为正确预测的正标签数量除以你正确预测的正标签数量加上你预测错误的正标签数量。
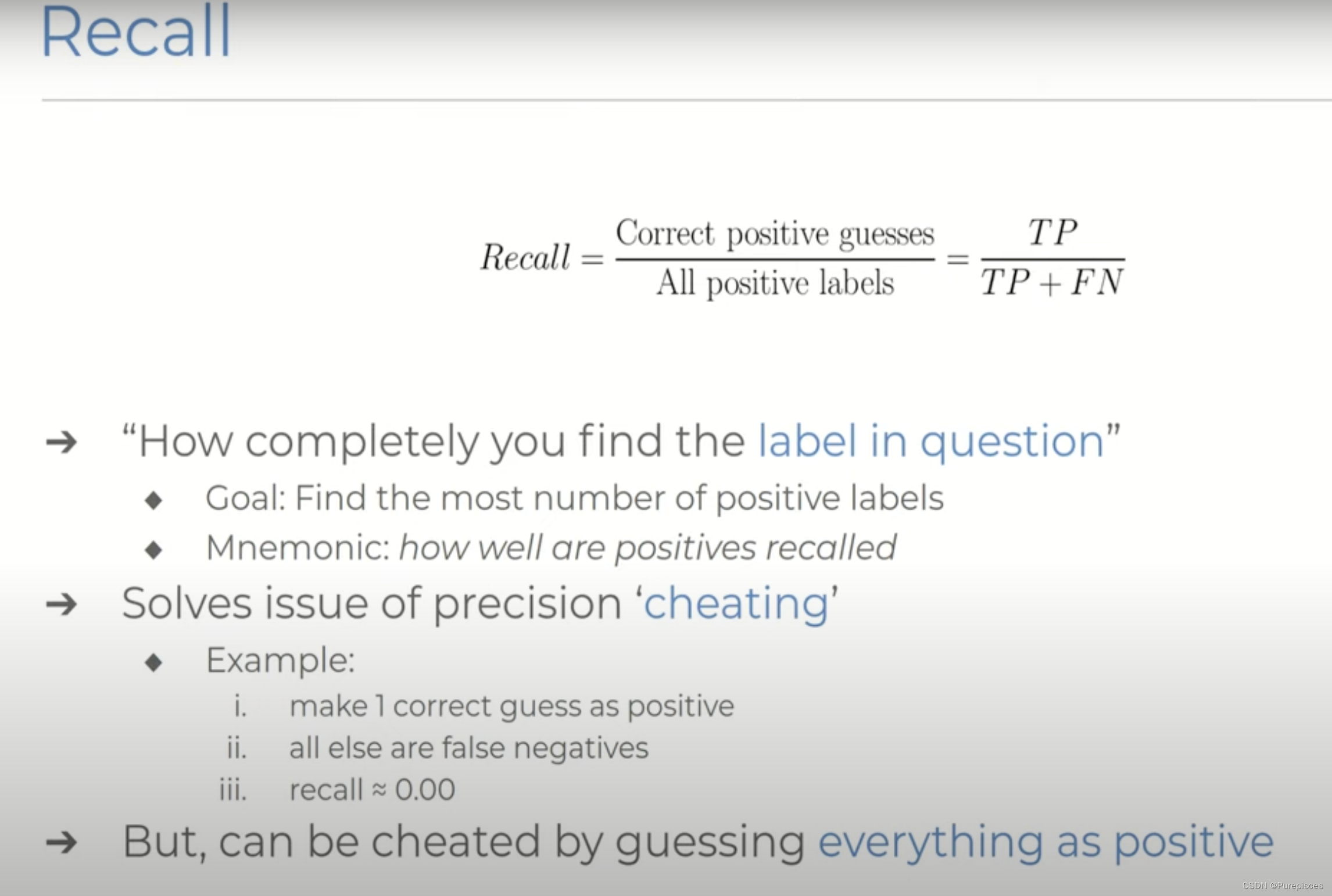
Recall = Correct Positive Guesses All Positive Labels = T P T P + F N \text{Recall} = \frac{\text{Correct Positive Guesses}}{\text{All Positive Labels}} = \frac{TP}{TP + FN} Recall=All Positive LabelsCorrect Positive Guesses=TP+FNTP
系统的目标是尽可能找到所有存在的正标签。
召回率的局限性
召回率仍然有一个问题,那就是通过自由地将任何事物标记为正例来扭曲分数。在极端情况下,只需将所有事物标记为正例就不会有任何假负例,从而获得完美的召回率分数。
Recall = TP TP + FN = 10 10 + 0 = 1 或 100 percent \text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}} = \frac{10}{10 + 0} = 1 \text{ 或 } 100 \ \text{percent} Recall=TP+FNTP=10+010=1 或 100 percent
为什么召回率是精确率的对应指标
精确率 vs. 召回率:
- 精确率:精确率衡量预测的正例中有多少实际上是正例。它关注正预测的准确性。
- 召回率 :召回率衡量实际正例中有多少被模型正确识别。它关注正预测的完整性。
由于精确率和召回率关注模型性能的不同方面,它们被认为是对应指标。提高其中一个有时会导致另一个的下降,因此它们相互平衡。
平衡精确率和召回率
现在应该很清楚,仅仅依靠精确率和召回率都有一些严重的缺陷,但事实上,一种指标防止了对另一种指标的作弊。为了获得100%的召回率,将导致精确率为零,反之亦然。通过这种方式,这两个指标相互补充,提出了一个问题:我们是否可以设计一个系统同时优化这两个分数。我们希望将预测的质量和完整性结合成一个分数。
虽然精确率关注正预测的正确性,但召回率关注正预测的完整性。
精确率和召回率之间的权衡:
当你调整将实例分类为正例的阈值时,会对精确率和召回率产生影响,通常是相反的方向:
提高精确率:
为了提高精确率,你可能会设置更高的阈值来将实例分类为正例。这意味着模型在标记正例时会更加保守,从而减少假正例(FP)。然而,这种保守性也意味着它可能会错过一些真正例(TP),从而降低召回率。
示例: 一个分类电子邮件为垃圾邮件的模型可能非常保守,只有在非常确定时才将电子邮件标记为垃圾邮件。这减少了非垃圾邮件被错误标记为垃圾邮件的数量(高精确率),但可能会错过一些实际的垃圾邮件(低召回率)。提高召回率:
为了提高召回率,你可能会设置更低的阈值来将实例分类为正例。这使得模型在标记正例时更加宽松,从而减少假负例(FN)。然而,这种宽松性增加了将非正例标记为正例的可能性,从而降低精确率。
示例: 同样的垃圾邮件分类器可能会更宽松地标记电子邮件为垃圾邮件,捕捉更多的实际垃圾邮件(高召回率),但也会错误地标记更多非垃圾邮件(低精确率)。

F1分数
这就是F1分数的作用。F1分数定义为精确率和召回率的调和平均数。该分数基本上询问预测的质量有多好以及我们从数据集中预测标签的完整性。重要的是,F1分数并不简单地使用算术平均数来组合分数。事实上,这对于我们之前讨论的所谓作弊情况会是相当不利的。调和平均数将分数偏向两个组成分数中较低的一个,这实际上惩罚了精确率和召回率彼此之间的严重不一致,并正确反映了当它们中的任何一个接近零时的情况。
F1 = 2 ⋅ Precision ⋅ Recall Precision + Recall = 2 ⋅ T P 2 ⋅ T P + F P + F N \text{F1} = 2 \cdot \frac{\text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}} = 2 \cdot \frac{TP}{2 \cdot TP + FP + FN} F1=2⋅Precision+RecallPrecision⋅Recall=2⋅2⋅TP+FP+FNTP
为什么F1分数不使用算术平均数?
考虑以下场景:
- 数据集: 10个正例和90个负例
- 模型预测: 预测所有为正例
结果预测为:
- 真正例(TP): 10
- 假正例(FP): 90
- 真负例(TN): 0
- 假负例(FN): 0
计算精确率和召回率:
- 精确率: T P T P + F P = 10 10 + 90 = 0.1 \frac{TP}{TP + FP} = \frac{10}{10 + 90} = 0.1 TP+FPTP=10+9010=0.1
- 召回率: T P T P + F N = 10 10 + 0 = 1 \frac{TP}{TP + FN} = \frac{10}{10 + 0} = 1 TP+FNTP=10+010=1
精确率和召回率的算术平均数为:
0.1 + 1 2 = 0.55 \frac{0.1 + 1}{2} = 0.55 20.1+1=0.55
这个结果误导性地表明了中等表现。然而,作为精确率和召回率的调和平均数,F1分数计算如下:
F 1 = 2 × 0.1 × 1 0.1 + 1 ≈ 0.18 F1 = 2 \times \frac{0.1 \times 1}{0.1 + 1} \approx 0.18 F1=2×0.1+10.1×1≈0.18
这表明F1分数通过惩罚精确率和召回率之间的极端不平衡,更准确地反映了模型的糟糕表现。

结论
F1分数是我们比较系统的最常用指标之一,在大多数情况下,它是衡量模型性能的良好指标。然而,在一些情况下,尤其是处理多类别系统时,它并不那么适用,因为对于每个不同类别的性能同样重要。此外,该指标在计算中不包含真负例,因为精确率和召回率分别不包括它们。
通常在二分类问题中,一个类别是主要关注的。这通常是正类,例如检测欺诈、识别疾病或识别垃圾邮件。示例:在疾病检测中,主要关注的是识别疾病病例(正类)。错过一个疾病病例(假负例)通常比错误地将一个健康人识别为疾病患者(假正例)更为严重。
在多类别分类中,有两个以上的类别,并且每个类别的性能同样重要。示例:在图像分类任务中,类别如猫、狗和鸟,将猫错误分类为狗与将狗错误分类为鸟同样重要。
