[从0开始轨迹预测][NMS]：NMS的应用（目标检测、轨迹预测）

非极大值抑制（Non-Maximum Suppression，简称NMS）是一种在计算机视觉中广泛应用的算法，主要用于消除冗余和重叠的边界框。在目标检测 任务中，尤其是在使用诸如R-CNN系列的算法时，会产生大量的候选区域，而这些区域可能存在大量的重叠。为了解决这个问题，使用NMS算法来保留最有可能的区域，同时抑制其他冗余或重叠的区域。

1. NMS在目标检测领域的应用

非极大值抑制在目标检测领域的基本原理和步骤如下：

对于每个类别，按照预测框的置信度进行排序，将置信度最高的预测框作为基准。
从剩余的预测框中选择一个与基准框的重叠面积最大的框，如果其重叠面积大于一定的阈值，则将其删除。
对于剩余的预测框，重复步骤2，直到所有的重叠面积都小于阈值，或者没有被删除的框剩余为止。

通过这样的方式，NMS可以过滤掉所有与基准框重叠面积大于阈值的冗余框，从而实现检测结果的优化。值得注意的是，NMS的阈值通常需要根据具体的数据集和应用场景进行调整，以兼顾准确性和召回率。

python 复制代码

# NMS Python 简单实现
import numpy as np

def nms(dets, thresh):
    x1 = dets[:, 0]
    y1 = dets[:, 1]
    x2 = dets[:, 2]
    y2 = dets[:, 3]
    scores = dets[:, 4]

    areas = (x2 - x1 + 1) * (y2 - y1 + 1)
    order = scores.argsort()[::-1]

    keep = []
    while order.size > 0:
        i = order[0]
        keep.append(i)

        xx1 = np.maximum(x1[i], x1[order[1:]])
        yy1 = np.maximum(y1[i], y1[order[1:]])
        xx2 = np.minimum(x2[i], x2[order[1:]])
        yy2 = np.minimum(y2[i], y2[order[1:]])

        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        inter = w * h
        ovr = inter / (areas[i] + areas[order[1:]] - inter)

        inds = np.where(ovr <= thresh)[0]
        order = order[inds + 1]

    return keep

这段代码首先计算所有候选框的面积和分数，然后按照分数对候选框进行排序。然后，它进入一个循环，每次循环中，它都会选择当前分数最高的框，并将其添加到保留列表中。然后，它会计算这个框与其他所有框的重叠区域，并计算这些重叠区域与各自框的面积之比（即IoU）。如果这个比值大于给定的阈值，那么就会将对应的框从候选列表中删除。这个过程会一直重复，直到所有的框都被处理完毕。

2. NMS在轨迹预测领域的应用

NMS在轨迹预测中的应用，主要是用来处理预测结果中的冗余和重叠的轨迹，对于一些方法，模型预测出大量的候选轨迹，这些轨迹可能存在大量的重叠。为了解决这个问题，可以使用上述NMS算法来保留最有可能的轨迹，同时抑制其他冗余或重叠的轨迹。

假设对某个场景中的某辆车使用模型预测了64条或更多的轨迹，以很好地捕获多模态性，同时每条轨迹对应一个置信度，所有轨迹置信度总和为1。但最终输出时，我们一般仅输出6条轨迹（下游 or 打榜需求），如果直接选择置信度最高的6条轨迹会存在问题，比如说这六条轨迹靠的很近，无法体现多模态性。因此，我们需要使用NMS来选择最终的轨迹：

将轨迹按照置信度从高到低排序。
计算每两条轨迹之间最后一个点的距离，会产生一个距离矩阵。
依次按照置信度高低选取轨迹，比如第一次选择排名第一的轨迹，后面再选择轨迹时需要跟已经选择的所有判断距离是否大于某个阈值，如果小于该阈值，说明存在已选的轨迹与当前要被选择的轨迹很类似，则放弃选择该轨迹。

这样，通过NMS，我们可以从大量的预测轨迹中选择出最具代表性的轨迹，从而提高轨迹预测的效果。

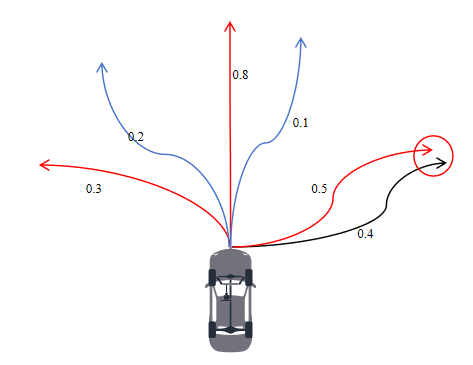
从图中6条轨迹中选择出3条，如果按照置信度来选，应该选择0.8，0.5，0.4的轨迹，但由于0.5和0.4两条轨迹靠的太近（小于某个阈值）因此最终选择的轨迹为0.8，0.5，0.3三条轨迹。

python 复制代码

def batch_nms(pred_trajs, pred_scores, dist_thresh, num_ret_modes=6):
    """

    Args:
        pred_trajs (batch_size, num_modes, num_timestamps, 7)
        pred_scores (batch_size, num_modes):
        dist_thresh (float):
        num_ret_modes (int, optional): Defaults to 6.

    Returns:
        ret_trajs (batch_size, num_ret_modes, num_timestamps, 5)
        ret_scores (batch_size, num_ret_modes)
        ret_idxs (batch_size, num_ret_modes)
    """
    
    batch_size, num_modes, num_timestamps, num_feat_dim = pred_trajs.shape

    sorted_idxs = pred_scores.argsort(dim=-1, descending=True)
    bs_idxs_full = torch.arange(batch_size).type_as(sorted_idxs)[:, None].repeat(1, num_modes)
    sorted_pred_scores = pred_scores[bs_idxs_full, sorted_idxs]  # 对score从大到小排序
    sorted_pred_trajs = pred_trajs[bs_idxs_full, sorted_idxs]  # (batch_size, num_modes, num_timestamps, 7)
    sorted_pred_goals = sorted_pred_trajs[:, :, -1, :]  # (batch_size, num_modes, 7)  最后一个点

    dist = (sorted_pred_goals[:, :, None, 0:2] - sorted_pred_goals[:, None, :, 0:2]).norm(dim=-1)  # 64*64 的距离矩阵
    point_cover_mask = (dist < dist_thresh)

    point_val = sorted_pred_scores.clone()  # (batch_size, N)
    point_val_selected = torch.zeros_like(point_val)  # (batch_size, N)

    ret_idxs = sorted_idxs.new_zeros(batch_size, num_ret_modes).long()
    ret_trajs = sorted_pred_trajs.new_zeros(batch_size, num_ret_modes, num_timestamps, num_feat_dim)
    ret_scores = sorted_pred_trajs.new_zeros(batch_size, num_ret_modes)
    bs_idxs = torch.arange(batch_size).type_as(ret_idxs)

    for k in range(num_ret_modes):
        cur_idx = point_val.argmax(dim=-1) # (batch_size)
        ret_idxs[:, k] = cur_idx

        new_cover_mask = point_cover_mask[bs_idxs, cur_idx]  # (batch_size, N)
        point_val = point_val * (~new_cover_mask).float()  # (batch_size, N)
        point_val_selected[bs_idxs, cur_idx] = -1
        point_val += point_val_selected

        ret_trajs[:, k] = sorted_pred_trajs[bs_idxs, cur_idx]
        ret_scores[:, k] = sorted_pred_scores[bs_idxs, cur_idx]

    bs_idxs = torch.arange(batch_size).type_as(sorted_idxs)[:, None].repeat(1, num_ret_modes)

    ret_idxs = sorted_idxs[bs_idxs, ret_idxs]
    return ret_trajs, ret_scores, ret_idxs