代码随想录Day70（图论Part06）

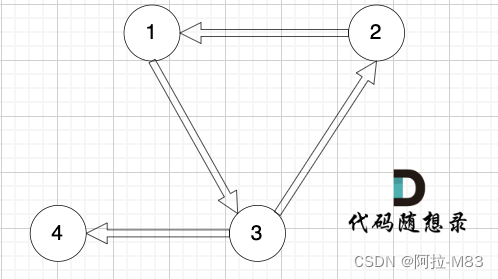
108.冗余连接

题目：108. 冗余连接 (kamacoder.com)

思路：每次更新输出的边，来保证删除的是输入中最后出现的那条边。关键是，我要知道哪条边可以删除，而且是在join的时候就判断

尝试（难得AC）

java 复制代码

import java.util.Scanner;

public class Main {
    private static int[] father;
    private static int s1 =0;
    private static int t1 =0;
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        int n = scanner.nextInt(); // 节点数量

        // 初始化并查集
        father = new int[n + 1];
        init(n);


        // 读取边并构建并查集
        for (int i = 0; i < n; i++) {
            int s = scanner.nextInt();
            int t = scanner.nextInt();
            join(s, t);
        }
        System.out.println(s1+" "+t1);
        

    }

    // 并查集初始化
    private static void init(int n) {
        for (int i = 1; i <= n; i++) {
            father[i] = i;
        }
    }

    // 并查集里寻根的过程
    private static int find(int u) {
        if (u != father[u]) {
            father[u] = find(father[u]);
        }
        return father[u];
    }

    // 判断 u 和 v 是否找到同一个根
    private static boolean isSame(int u, int v) {
        return find(u) == find(v);
    }

    // 将 v -> u 这条边加入并查集
    private static void join(int u, int v) {
        int rootU = find(u);
        int rootV = find(v);
        if (rootU != rootV) {
            father[rootV] = rootU;
        }else{
            s1 = u;
            t1 = v;
        }
    }
}

小结

基于【寻找存在的路径】代码改造，如果发现输入的（s，t）指向同一个根，说明是冗余连接，通过s1，t1每次join的时候更新

109.冗余连接||

题目：109. 冗余连接II (kamacoder.com)

思路：按照题目的意思，至少有一条边是可以删除的，我想通过fa数组，找到fa中最少被指向的元素，删掉该边，或者是说，输出该边

在遍历father数组时，还需要记录是哪条边，或许可以用set来存储

尝试（标题4）

java 复制代码

import java.util.*;

class Main {
    public static int[] father;
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        
        father = new int[n + 1];
        init(n);
        
        for (int i = 0; i < n; i++) { // 修正循环范围
            int s = scanner.nextInt();
            int t = scanner.nextInt();
            join(s, t);
        }
        
        int[] count = new int[n + 1];
        Map<Integer, Integer> map = new HashMap<>(); // 使用 Map
        
        for (int i = 1; i <= n; i++) { // 修正循环范围
            int root = find(i); // 确保父节点是根节点
            count[root]++;
            map.put(i, root);
        }
        
        for (int i = 1; i <= n; i++) { // 修正循环范围
            if (count[i] == 1) {
                System.out.println(map.get(i) + " " + i);
            }
        }
    }
    
    public static void init(int n) {
        for (int i = 1; i <= n; i++) {
            father[i] = i;
        }
    }
    
    public static int find(int u) {
        if (u != father[u]) {
            father[u] = find(father[u]);
        }
        return father[u];
    }
    
    public static void join(int u, int v) {
        int rootU = find(u);
        int rootV = find(v);
        if (rootU != rootV) {
            father[rootU] = rootV;
        }
    }
}

答案

java 复制代码

import java.util.*;

public class Main {
    public static int n;
    public static int[] father;
    public static int[] inDegree;
    
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        
        father = new int[n + 1];
        inDegree = new int[n + 1];
        
        List<int[]> edges = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            int s = scanner.nextInt();
            int t = scanner.nextInt();
            inDegree[t]++;
            edges.add(new int[]{s, t});
        }
        
        List<Integer> vec = new ArrayList<>(); // 记录入度为2的边（如果有的话就两条边）
        // 找入度为2的节点所对应的边，注意要倒序，因为优先删除最后出现的一条边
        for (int i = n - 1; i >= 0; i--) {
            if (inDegree[edges.get(i)[1]] == 2) {
                vec.add(i);
            }
        }
        if (!vec.isEmpty()) {
            // 放在vec里的边已经按照倒序放的，所以这里就优先删vec.get(0)这条边
            if (isTreeAfterRemoveEdge(edges, vec.get(0))) {
                System.out.println(edges.get(vec.get(0))[0] + " " + edges.get(vec.get(0))[1]);
            } else {
                System.out.println(edges.get(vec.get(1))[0] + " " + edges.get(vec.get(1))[1]);
            }
            return;
        }
        
        // 处理情况三
        // 明确没有入度为2的情况，那么一定有有向环，找到构成环的边返回就可以了
        getRemoveEdge(edges);
    }
    
    // 并查集初始化
    public static void init() {
        for (int i = 1; i <= n; ++i) {
            father[i] = i;
        }
    }
    
    // 并查集里寻根的过程
    public static int find(int u) {
        return u == father[u] ? u : (father[u] = find(father[u]));
    }
    
    // 将v->u 这条边加入并查集
    public static void join(int u, int v) {
        u = find(u);
        v = find(v);
        if (u == v) return;
        father[v] = u;
    }
    
    // 判断 u 和 v是否找到同一个根
    public static boolean same(int u, int v) {
        u = find(u);
        v = find(v);
        return u == v;
    }
    
    // 在有向图里找到删除的那条边，使其变成树
    public static void getRemoveEdge(List<int[]> edges) {
        init(); // 初始化并查集
        for (int i = 0; i < n; i++) { // 遍历所有的边
            if (same(edges.get(i)[0], edges.get(i)[1])) { // 构成有向环了，就是要删除的边
                System.out.println(edges.get(i)[0] + " " + edges.get(i)[1]);
                return;
            } else {
                join(edges.get(i)[0], edges.get(i)[1]);
            }
        }
    }
    
    // 删一条边之后判断是不是树
    public static boolean isTreeAfterRemoveEdge(List<int[]> edges, int deleteEdge) {
        init(); // 初始化并查集
        for (int i = 0; i < n; i++) {
            if (i == deleteEdge) continue;
            if (same(edges.get(i)[0], edges.get(i)[1])) { // 构成有向环了，一定不是树
                return false;
            }
            join(edges.get(i)[0], edges.get(i)[1]);
        }
        return true;
    }
}

小结

要考虑的情况有三种

有入度为2的节点
- 删除前，先判断删除后，本图能否成为有向树
- 删哪个都可以时，就选择顺序靠后的删除

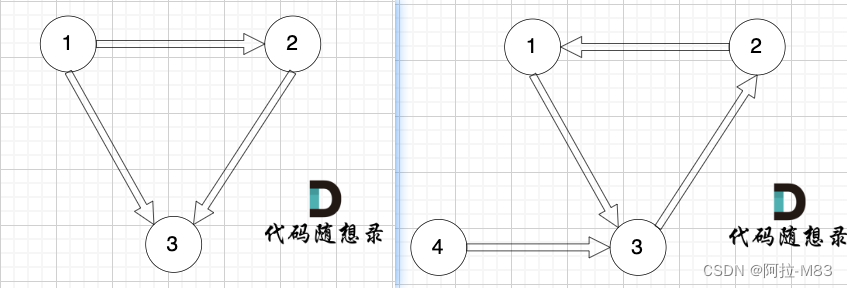
没有入度为2的节点
- 图中有环，删掉构成环的边