一、引言
基金是一种非常受欢迎的投资工具，由于其具有风险分散、专业管理等特点，越来越多的投资者选择将资金投入基金市场。然而，基金的表现却受到很多因素的影响，如股票市场的整体表现、基金管理人员的能力、基金规模、基金管理费率等。因此，对基金的投资回报率进行研究和预测，对于投资者来说具有非常重要的意义。。。。
二、研究综述
近些年,开放式基金的规模逐年增加,已经逐渐成为中国金融市场重要组成部分。基金经理作为基金投资管理的主要负责人,其投资风险行为对于基金的长期业绩的稳定性具有重要影响作用。针对基金经理的投资风险行为的机理分析和预测,可以给投资者和监管者的决策提供参考依据,对于开放式基金的长期良性地发展具有重要意义。国内外大多数学者,采用基金业绩的波动,即基金业绩的标准差,作为基金经理投资风险的衡量标准。研究发现,基金经理会根据自己历史的相对排名对将来的投资风险进行调整。。。。
三、理论
多元线性回归具有非常广泛的应用范围，但在实 际预测中对存在类别变量设置不充分或多重共线性 问题，导致统计模型缺乏精度和稳健性。由此，本文 对如何精准且高效的排除多重共线性影响，并合理地 将分类变量转化为虚拟变量，提升多元线性回归模型 精度作了进一步探索，并将其应用于基金预测上。。。。
ARIMA模型的全称是求和自回归移动平均（autoregressive integrated moving average）模型，简记为ARIMA(p,d,q)模型，是最常见的时间序列预测分析方法。利用历史数据可以预测未来的情况。。。。
四、实证分析
基金是华安中证光伏产业交易型开放型指数证券投资基金（159618）。本次分析的数据从2022年4月25日到2023年4月28日，一共包括248条数据。接下来进行数据的展示：
python
data1<- read.csv("JJSJ.csv")
data1
#####Descriptive statistical analysis
summary(data1)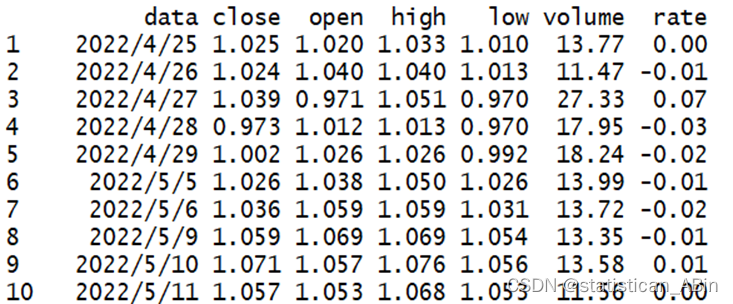
数据中包括了数据日期（data）、收盘价(close)、开盘(open)价、最高点(high)、最低点(low)、交易量volume以及最后的涨幅(rate)。
接下来使用summary()函数对数据做一个整体性描述。具体描述性统计如下，其中包括了各个变量的最大值、最小值、中位数、1/4分位数和3/4分位数等，如图所示。
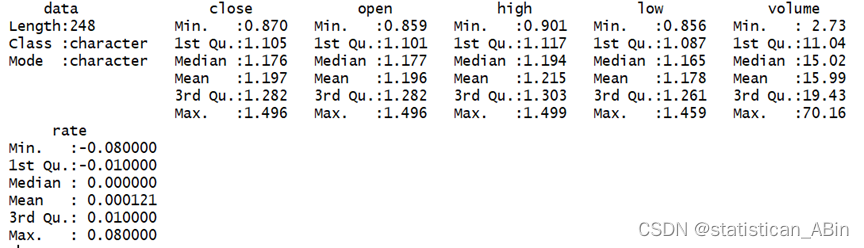
接下来进行数据的可视化展示：
我们首先画出基金收盘价的柱状图查看
R
head(price,n=10)
barplot(head(price,n=100),xlab="data",ylab="close_price",col="pink",main="Fund closing price",border="white")
接下来画出基金开盘价的折线图
从以上两幅图我们大致可以看出，随着大体趋势的变化，基金收盘价在逐步上升，而基金开盘价在逐步下降。接下来画出所有特征的箱线图来查看
R
par(mfrow = c(3, 2))
boxplot(data1$open, main = "Fund opening price",col = "lightblue", border = "blue")
boxplot(data1$high, main = "Fund's highest point price",col = "lightblue", border = "blue")
boxplot(data1$low, main = "The lowest point price of the fund",col = "lightblue", border = "blue")
boxplot(data1$close, main = "Fund closing price",col = "lightblue", border = "blue")
boxplot(data1$volume, main = "Fund trading volume",col = "lightblue", border = "blue")
boxplot(data1$rate, main = "Fund change rate",col = "lightblue", border = "blue")
随后我们通过相关系数热力图和相关系数具体结果来进行分析：
R
library(ggcorrplot)
corr = cor(data1[, c(2:7)])
p.mat <- cor_pmat(data1[, c(2:7)], use = "complete", method = "pearson")
ggcorrplot(corr, hc.order = TRUE,colors = c("red", "green","blue"), type = "lower", lab = TRUE, p.mat = p.mat,
insig = "blank")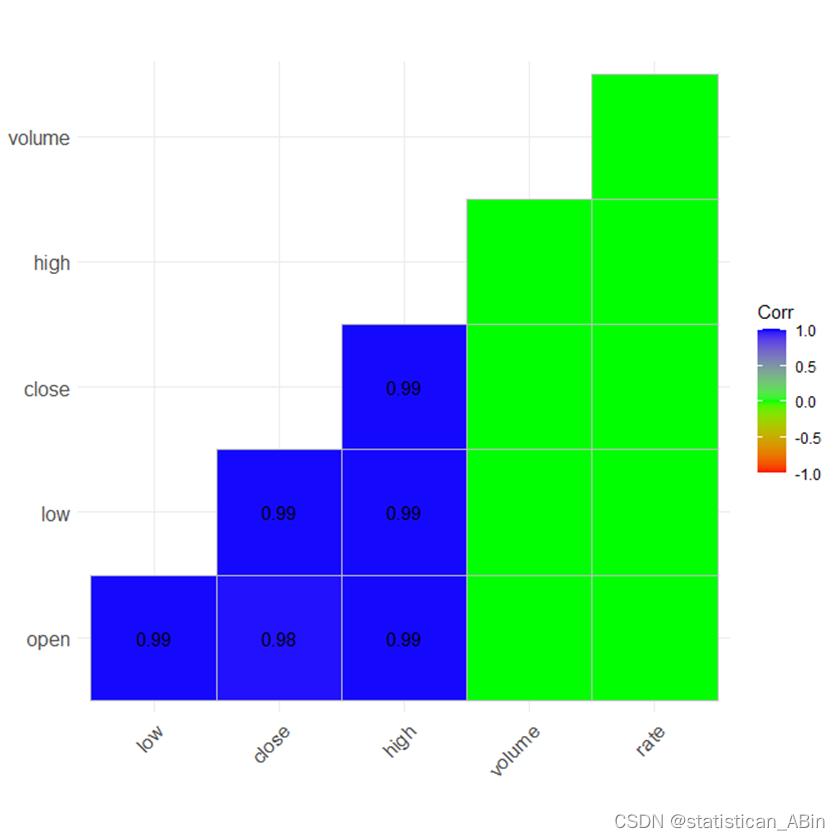
从图6可以看出，收盘价与最高点、最低点以及开盘价最为相关，与其他特征暂时没有那么强的相关性。接下来绘制数据集中各个变量之间的散点图、直方图和密度图等：
从上面的结果我们可以看出与之前的热力图的结果是一致的。接下来正式进入多元线性回归。我们将close作为"y"，其他全部当作特征。
R
##Stepwise regression
fit1 <- step(fit,direction = "backward")
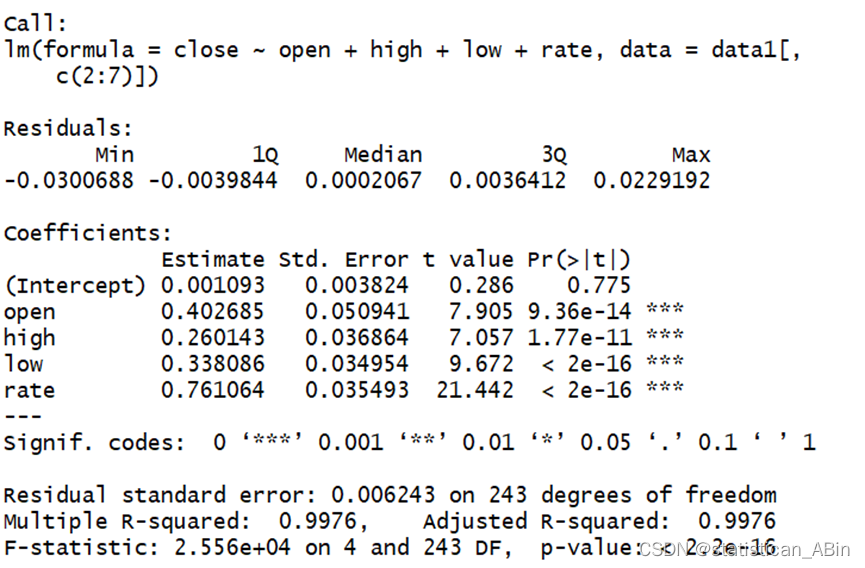
summary(fit1)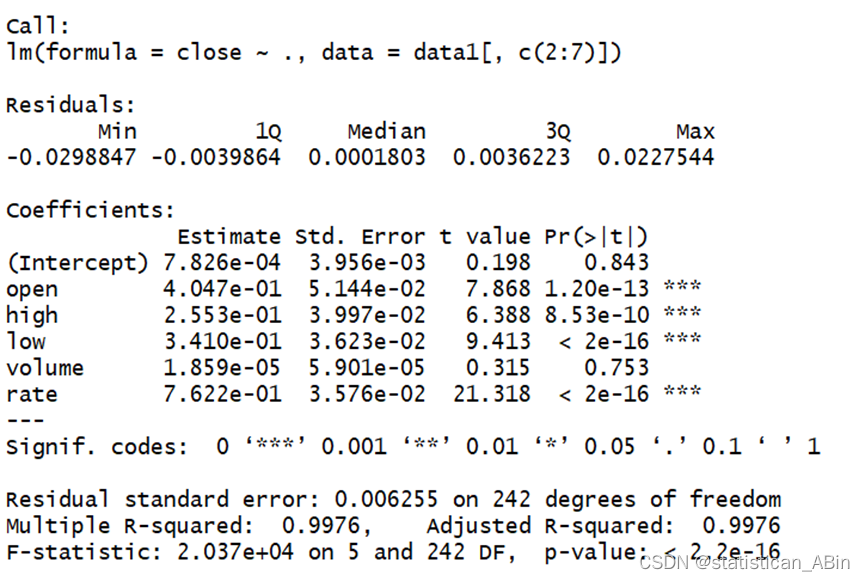
从回归结果来看，开盘价，最低最高点价格以及涨幅都是显著性的。接下来进行逐步回归，查看AIC值：
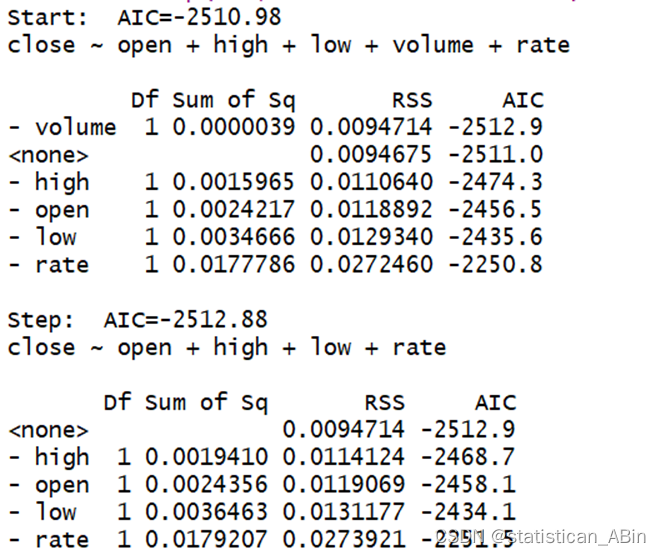
从图中可以看出，我们剔除了volume变量。随后进行相应的检验：
异方差检验
R
#Heteroscedasticity test
library(foreign)
library(zoo)
lmtest::bptest(fit1)
###Autocorrelation test DW is generally used for time series data
library(lmtest)
dwtest(fit)异方差检验结果
|--------------------------------------|
| Stufentsized Breusch-Pagan test |
| Data: fit2_step |
| BP= 29.157, df=4 , p_value=7.265e-06 |
自相关检验结果
|----------------------------------------------------------------|
| Durbin-Watson test |
| Data: fit |
| DW = 2.1237, p-value = 0.8051 |
| alternative hypothesis: true autocorrelation is greater than 0 |
多重共线性检验
|-------------------------------------------|
| open high low rate |
| 271.732170 144.403137 119.023976 3.668331 |
模型的残差也进行正态性检验
接下来直接画出残差图来看
R
par(mfrow=c(2,2))
plot(fit1)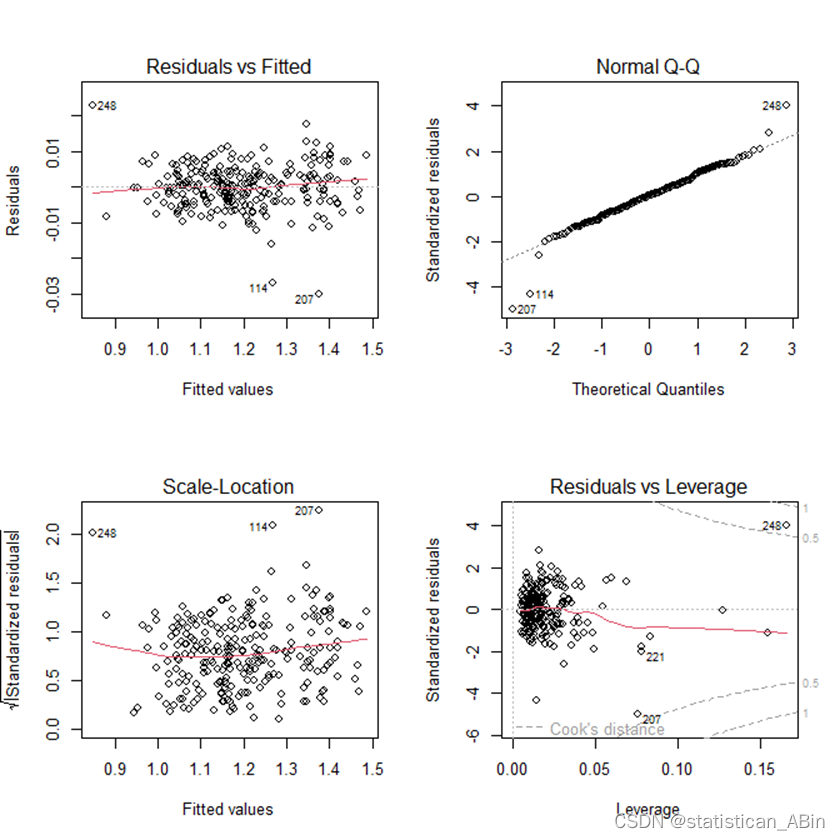
接下来针对close进行时间序列分析和预测：
R
#White noise test
for(i in 1:3) print(Box.test(HL,type = "Ljung-Box",lag=6*i))
par(mfrow = c(1, 2))
acf(HL,main='ACF',lag.max = 12)
pacf(HL,main='PACF',lag.max = 12)表 时间序列数据纯随机检验
|-----------------|---------------|-------------|
| 滞后期数 | 卡方统计量 | P值 |
| 滞后6期P值 | 1200.3 | 0.000 |
| 滞后12期P值 滞后18期P值 | 2065.9 2658.4 | 0.000 0.000 |
随后画出自相关图和偏自相关图查看：
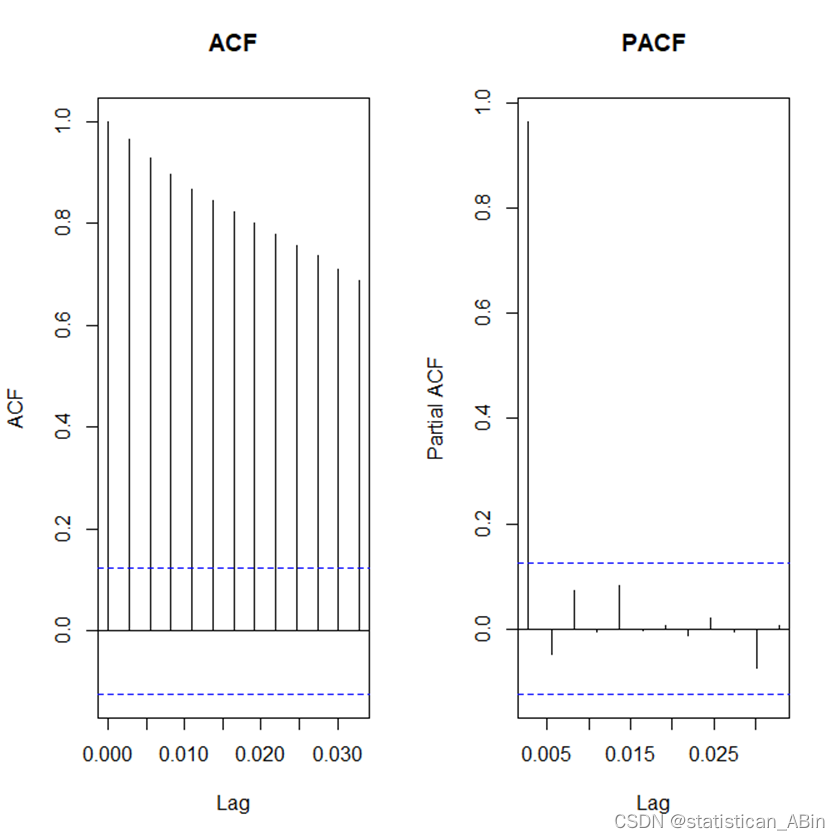
下面进行ADF检验，查看其平稳性：
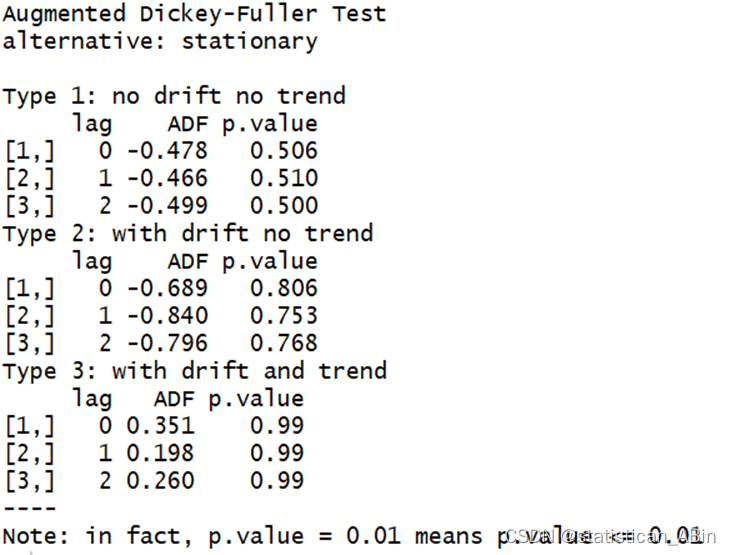从结果看来，序列数据并不平稳，需要进行差分测试，在差分测试后需要对序列数据进行二阶差分：
随后运用auto.arima()函数自动定阶：
R
###Automatic ranking
auto.arima(HL)
###Model fitting
HL.fit<-auto.arima(HL)
HL.fit
R
arima<-auto.arima(HL,trace=T)
accuracy(HL.fit)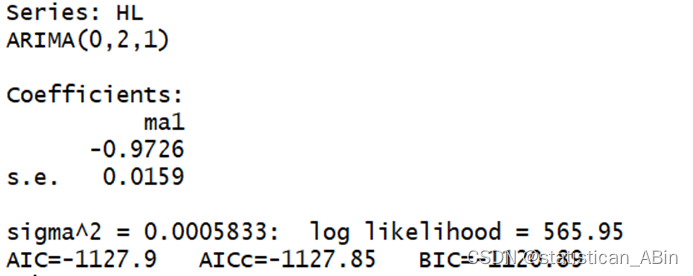
接下来进行模型比较和选择：
在模型选择完成之后还是需要进行相应的检验
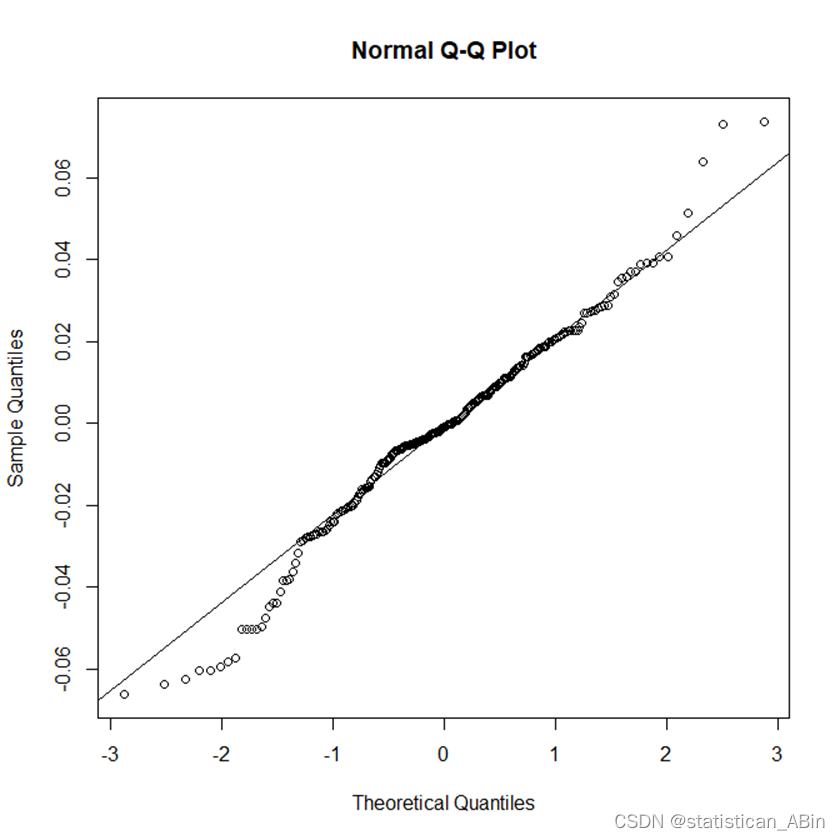
残差检验
|-----------------------------------------------|
| Box-Ljung test |
| data: HL.fit$residuals |
| X-squared = 0.21185, df = 1, p-value = 0.6453 |
接下来进行模型预测结果及可视化
R
###Model prediction 15 periods
per_HL<-forecast(HL.fit,h=15)
per_HL
plot(per_HL)
L1<-per_HL$fitted-1.96*sqrt(HL.fit $sigma2)
U1<-per_HL$fitted+1.96*sqrt(HL.fit $sigma2)
L2<-ts(per_HL$lower[,2])
U2<-ts(per_HL$upper[,2])
c1<-min(HL,L1,L2)
c2<-max(HL,L2,U2)
plot(HL,type = "p",pch=8,ylim = c(c1,c2))
lines(per_HL$fitted,col=2,lwd=2)
lines(per_HL$mean,col=2,lwd=2)
lines(L1,col=4,lty=2)
lines(L2,col=4,lty=2)
lines(U1,col=4,lty=2)
lines(U2,col=4,lty=2)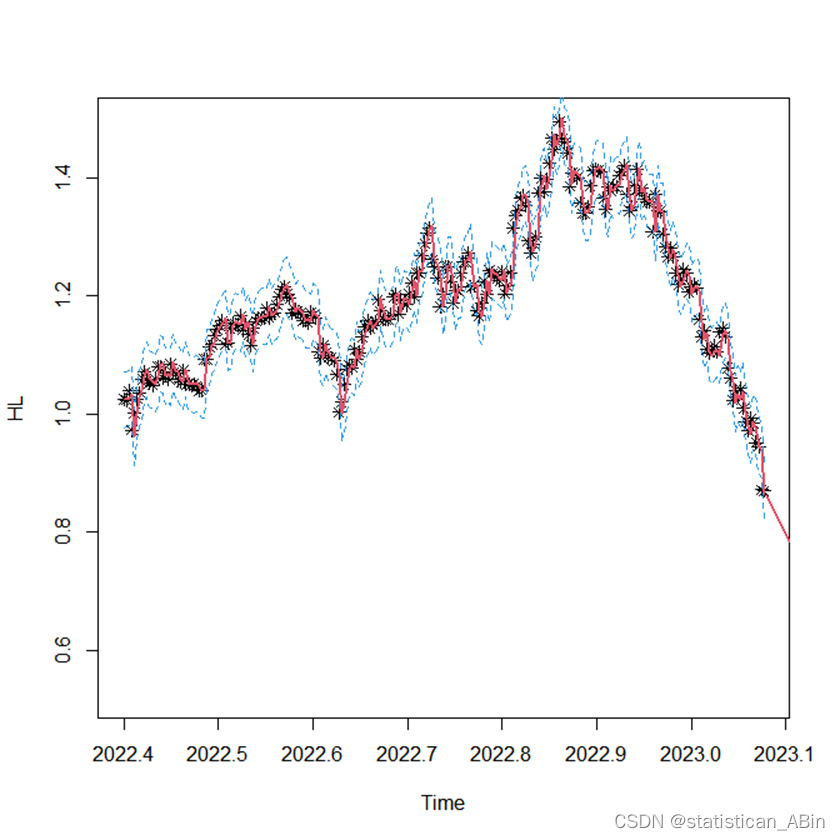
从上面具体数据和15期预测可视化我们都能看见，随着时间的变化，该基金的整体收盘价是逐渐下降的。
五、结论
本文使用了多元线性回归和时间序列预测方法对基金的表现进行研究和预测。具体步骤如下：
数据收集，多元线性回归分析：我们使用多元线性回归模型对基金的表现进行了分析，找出对基金收盘价影响最大的因素。时间序列预测：我们使用时间序列分析方法对基金的未来表现进行预测，包括基金的趋势和周期等。
参考文献：
- 徐聪. 基金经理投资风险行为机理分析和预测[D].东北大学,2014.
- 李盈盈.上海养老保险基金良性运营计算机仿真研究[J].科技信息,2014(01):62-63+106.
- 吴君槐,张丽萍.城乡居民医保整合背景下基于GM(1,1)模型的基金预测研究[J].中国集体经济,2022,No.718(26):103-107.
创作不易，希望大家多点赞关注评论！！！（类似代码或报告定制可以私信）