69. x 的平方根（简单）

69. x 的平方根

[1. 题目描述](#1. 题目描述)
2.详细题解
3.代码实现
- [3.1 Python](#3.1 Python)
- - 方法一：逐个遍历
  - 方法二：二分查找
- [3.2 Java](#3.2 Java)

1. 题目描述

2.详细题解

不能使用系统内置的函数，寻找某个数（假定为x）的算术平方根，并返回算术平方根的整数部分，最直观的方法是从0依次开始尝试所有小于等于x的数（假定为y），当y*y的积小于等于x时，继续遍历下一个数，直至y*y的积首次大于x时，此时y-1即为x的算术平方根的整数部分，如Python方法一逐个遍历实现。

上述方法遍历的过程中，每次仅能排除判断一个数字是否满足，有没有办法一次性判断或者排除多个数字呢？这就是二分查找算法，简单的说，即待查数据需有序，每次判断时折中取中间值进行对比，以判断目标值可能存在的那一半，从而快速定位目标值，每次判断可以排除一半的空间大小。具体算法如下：

Step1：前置条件：个已排序的数组 arr 和待查找的元素 target。；
Step2：初始化：两个指针 left 和 right，分别指向数组的起始和结束位置；
Step3：计算中间元素的索引： mid = (left + right) / 2；
Step4：比较中间元素 arr $mid$ 与 target；
如果 arr $mid$ == target，则找到目标值，返回 mid，程序结束；
如果 arr $mid$ < target，则目标值可能在 mid 的右侧，更新 left = mid + 1；
如果 arr $mid$ > target，则目标值可能在 mid 的左侧，更新 right = mid - 1；
Step5：当 left <= right 时，循环执行Step3_Step4.

对于此题，是计算算术平方根的整数部分，因此等价于寻找首次平方之和大于x的数，该数减1即为x的算术平方根（假定x的算术平方根为y.z,其中y为整数部分，z为小数部分，y*y的结果是小于x，而(y+1）*(y+1)是大于x的）。因此，针对此题，二分查找算法在返回值方面有一点点不同，应当返回最后的右指针指向的值，为什么呢？因为right为最后一次mid值大于x时减1的值，其它的mid值均小于x，故最后一次大于x的mid值减1即为目标整数，即right。实现详见Python方法二和Java实现。

3.代码实现

3.1 Python

方法一：逐个遍历

python 复制代码

class Solution:
    def mySqrt(self, x: int) -> int:
        left = 0
        while left * left <= x:
            left += 1
        return left-1

方法二：二分查找

python 复制代码

class Solution:
    def mySqrt(self, x: int) -> int:
        left, right = 0, x//2
        while left <= right:
            mid = (left + right) // 2
            mul = mid * mid
            if mul == x:
                return mid
            elif mul < x:
                left = mid + 1
            else:
                right = mid - 1
        return right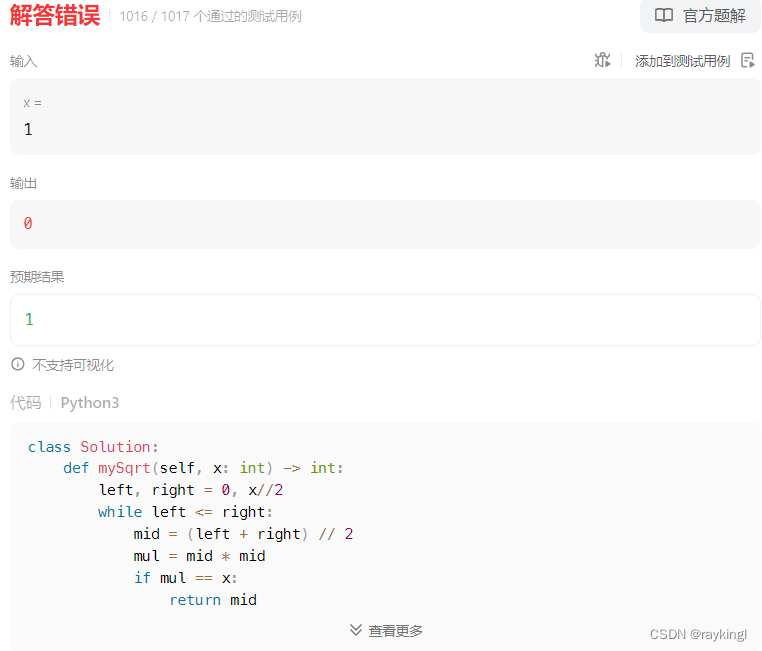

此时未通过x=1的测试用例，此时预期结果为1但返回0，仔细观察代码，right初始值为2整数x，对于1，结果为0，因此初始化出现了问题，优化如下：

python 复制代码

class Solution:
    def mySqrt(self, x: int) -> int:
        left, right = 0, x//2+1
        while left <= right:
            mid = (left + right) // 2
            mul = mid * mid
            if mul == x:
                return mid
            elif mul < x:
                left = mid + 1
            else:
                right = mid - 1
        return right

3.2 Java

java 复制代码

class Solution {
    public int mySqrt(int x) {
        int left = 0, right = x / 2 + 1;
        while (left <= right){
            int mid = (left + right) / 2;
            int mul = mid * mid;
            if (mul == x){return mid;}
            else if (mul < x){left = mid +1;}
            else{right = mid - 1;}
        }
        return right;
    }
}

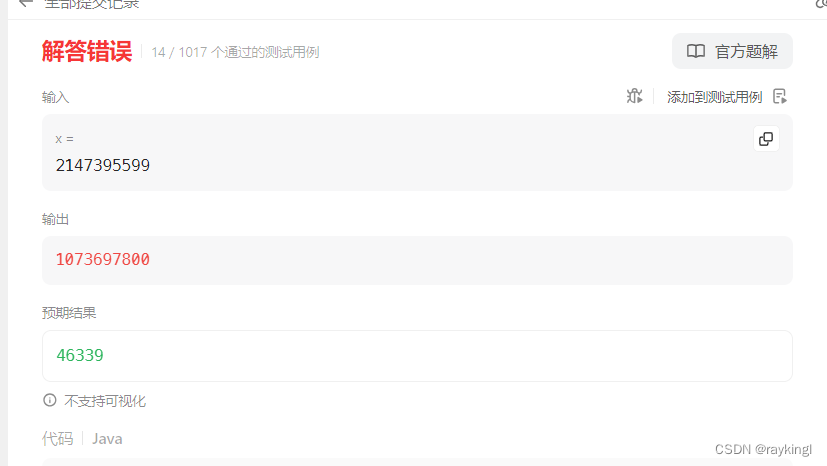
对于测试案例x=2147395599运行错误，直接返回了right初始值的结果，说明一直触发的是中间值平方小于x，这明显是错误的，考虑到Java是严格声明和定义数据类型的，因此错误在于内存溢出，超出Java的int类型的取值范围，故中间值使用long整型，优化如下：

java 复制代码

class Solution {
    public int mySqrt(int x) {
        int left = 0, right = (int)(x / 2 + 1);
        while (left <= right){
            int mid = (int) (left + right) / 2;
            long mul = (long)mid * mid;
            if (mul == x){
                return mid;
            }else if (mul < x){
                left = mid + 1;
            }else{
                right = mid - 1;
            }
        }
        return right;
    }
}

执行用时不必过于纠结，对比可以发现，对于python和java完全相同的编写，java的时间一般是优于python的；至于编写的代码的执行用时击败多少对手，执行用时和网络环境、当前提交代码人数等均有关系，可以尝试完全相同的代码多次执行用时也不是完全相同，只要确保自己代码的算法时间复杂度满足相应要求即可，也可以通过点击分布图查看其它coder的code。