论文阅读【时间序列】DSformer

arxive: DSformer: A Double Sampling Transformer for Multivariate Time Series Long-term Prediction

github: MTST

分类：多变量时间序列（Multivariate time series）

核心观点

多变量时间序列3个维度信息

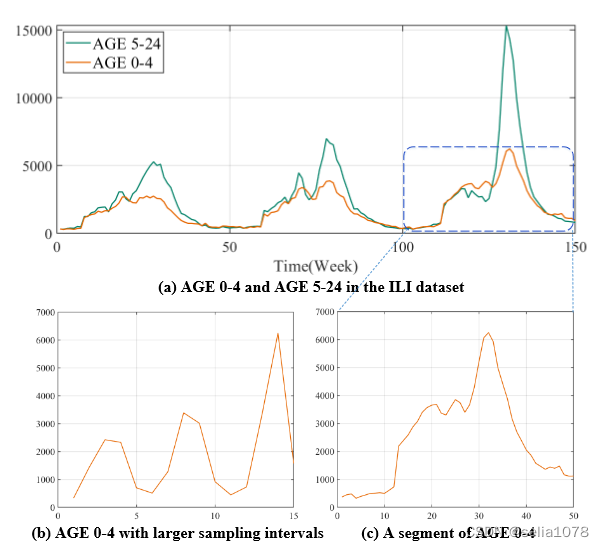
变量间关联（Variable correlation）：如Fig. 1(a)所示，不同变量具有相似的变化趋势 → \rightarrow → Variable Attention
全局信息（Global information）：如Fig. 1(b)所示，从全局来看，序列显示出一定的周期性 → \rightarrow → Down Sampling
局部信息（Local information）：如Fig. 1©所示，局部信息 → \rightarrow → Piecewise Sampling

个人观点：全局信息更多指周期项，局部信息更多指趋势项

整体框架

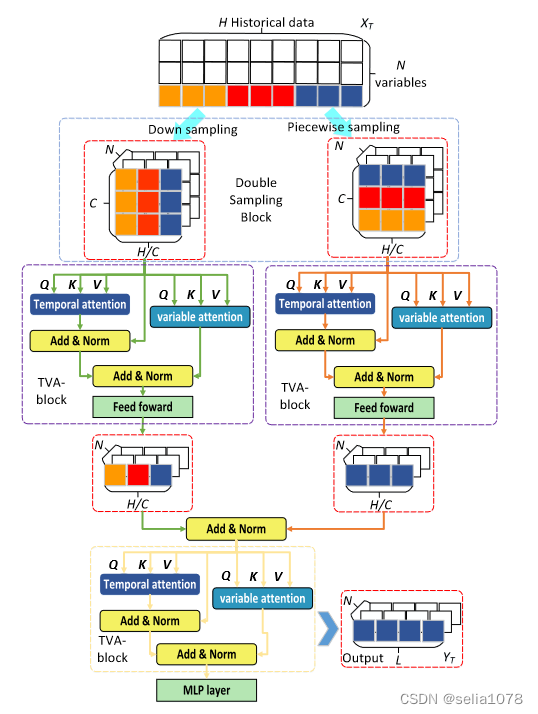
符号	含义
N	变量数
H	输入序列长度
L	输出序列长度
C	切分子序列数量

N 为变量数，H为输入序列长度，C是切分子序列的数量。

输入序列 X ∈ R N ∗ H X \in R^{N*H} X∈RN∗H，经过Down sampling得到 X d s ∈ R N ∗ C ∗ H C X_{ds} \in R ^{N * C * \frac{H}{C}} Xds∈RN∗C∗CH，经过Picewise Sampling得到 X p s ∈ R N ∗ C ∗ H C X_{ps} \in R ^{N * C * \frac{H}{C}} Xps∈RN∗C∗CH。

在TVA-block中进行Variable Attention和Temporal Attention。其中Temporal Attention中 Q ∈ R N ∗ C ∗ H C Q \in R ^{N * C * \frac{H}{C}} Q∈RN∗C∗CH, K ∈ R N ∗ H C ∗ C K \in R ^{N * \frac{H}{C} *C} K∈RN∗CH∗C；Variable Attention中 Q ∈ R H C ∗ C ∗ N Q \in R ^{\frac{H}{C} * C * N} Q∈RCH∗C∗N, K ∈ R ∗ H C ∗ N ∗ C K \in R ^{ * \frac{H}{C} *N *C} K∈R∗CH∗N∗C。

Temporal Attention是子序列之间，通过比较同一变量子序列的相似度计算注意力，Variable Attention是不同子序列之间，通过比较同一位置各个变量的相似度计算注意力。

随后，Temporal Attention和Variable Attention输出 X ′ ∈ R N ∗ C ∗ H C X' \in R ^{N * C * \frac{H}{C}} X′∈RN∗C∗CH被FFN压缩成 X ′ ∈ R N ∗ H C X' \in R ^{N * \frac{H}{C}} X′∈RN∗CH，然后相加。

最后，经过一个TVA-block整理来自不同视角的信息（Down sampling和Picewise Sampling）和MLP得到输出。

采样过程

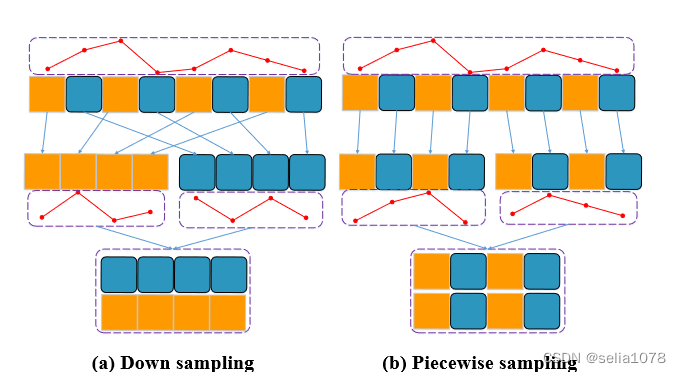
两种采样方式的区别在于如何将切分后的子序列重新排列。

Down Sampling: 每隔几个点取一个，用来捕获全局信息
X d s j = $x j , x j + H C , x j + 2 * H C , . . . , x j + ( C - 1 ) * H C$ X^j_{ds} = $x_j, x_{j+\\frac{H}{C}}, x_{j+2\*\\frac{H}{C}},..., x_{j+(C-1)\*\\frac{H}{C}}$ Xdsj= $xj,xj+CH,xj+2*CH,...,xj+(C-1)*CH$
Piecewise Sampling:
X p s j = $x 1 + ( j - 1 ) * C , x 2 + ( j - 1 ) * C , x 3 + ( j - 1 ) * C , . . . , x j * C$ X^j_{ps} = $x_{1+(j-1)\*C}, x_{2+(j-1)\*C}, x_{3+(j-1)\*C},..., x_{j\*C}$ Xpsj= $x1+(j-1)*C,x2+(j-1)*C,x3+(j-1)*C,...,xj*C$

TVA block

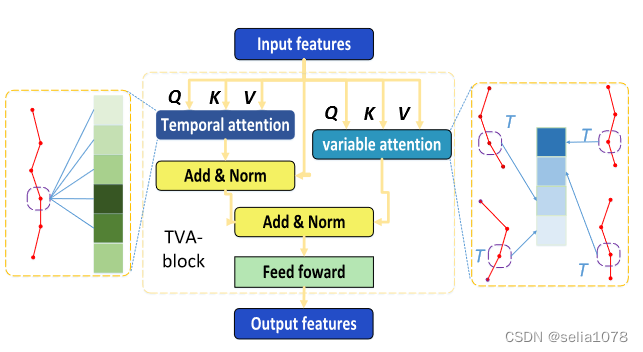
两种attention的主要区别在于X的维度变化：

Temporal Attention： Q ∈ R N ∗ C ∗ H C Q \isin R^{N * C * \frac{H}{C}} Q∈RN∗C∗CH, K ∈ R N ∗ H C ∗ C K \isin R^{N * \frac{H}{C} * C} K∈RN∗CH∗C
Variable Attention： Q ∈ R H C ∗ C ∗ N Q \isin R^{ \frac{H}{C} * C * N} Q∈RCH∗C∗N, K ∈ R H C ∗ N ∗ C K \isin R^{ \frac{H}{C} * N * C} K∈RCH∗N∗C