【Python机器学习】模型评估与改进——多分类指标

多分类问题的所有指标基本是上都来自于二分类问题，但是要对所有类别进行平均。多分类的精度被定义为正确分类的样本所占的比例。同样，如果类别是不平衡的，精度并不是很好的评估度量。

想象一个三分类问题，其中85%的数据点属于类别A，10%属于类别B，5%属于类别C。那么85%的精度并不能说明什么

一般来说，多分类结果比二分类结果更难理解。除了精度，常用的工具有混淆矩阵和分类报告。

下面应用于digits数据集中10中不同的手写数字进行分类的任务：

python 复制代码

from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix

digits=load_digits()
X_train,X_test,y_train,y_test=train_test_split(digits.data,digits.target,random_state=0)
lr=LogisticRegression().fit(X_train,y_train)

pred=lr.predict(X_test)
print('精度：{:.3f}'.format(lr.score(X_test,y_test)))
confusion=confusion_matrix(y_test,pred)
print('混淆矩阵：\n{}'.format(confusion))

模型精度为95.1%，这表示已经做得相当好了。混淆矩阵为我们提供了更多细节。而二分类相同，每一行对应真实标签，每一列对应于预测标签。

下图给出了更加明确的图像：

python 复制代码

scores_image=mglearn.tools.heatmap(
    confusion_matrix(y_test,pred)
    ,xlabel='预测表情'
    ,ylabel='真实标签'
    ,xticklabels=digits.target_names
    ,yticklabels=digits.target_names
    ,cmap=plt.cm.gray_r
    ,fmt='%d'
)
plt.title('混淆矩阵')
plt.gca().invert_yaxis()
plt.show()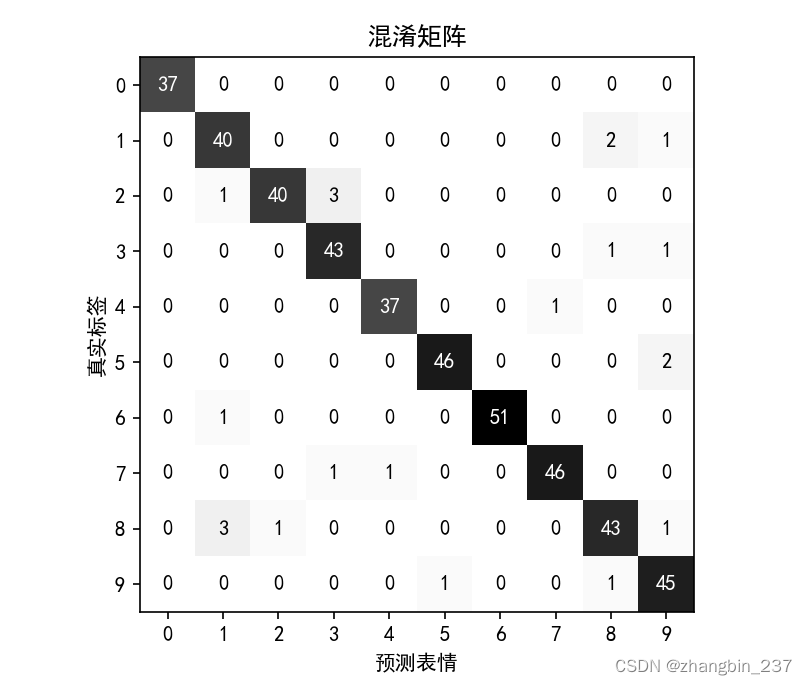

对于第一个类别（0），它包含37个样本，所有样本都被划为类别0，并且没有其他数字被误分类为类别0。

利用classification_report函数，我们可以计算每个类别的准确率、召回率和f-分数：

python 复制代码

print(classification_report(y_test,pred))

可以看到，类别0的准确率和召回率都是完美的100%，因为这个类别中没有混淆。另一方面，对于类别7，准确率为100%，这是因为没有其他类别被误分类为7，而类别6没有假反例，所以召回率为100%。还可以看到，类别8和类别3的表现特别不好。

对于多分类问题中的不平衡数据集，最常用的指标就是多分类版本的f-分数。多分类f-分数背后的思想是：对每个类别计算一个二分类f-分数，其中该类别为正类，其他所有类别为反类，然后使用以下策略之一对这些按照类别f-分数进行平均：

1、"宏"平均：计算未加权的按类别f-分数。它对所有类别给出相同的权重，无论类别中的样本量大小；

2、"加权"平均：以每个类别的支持作为权重来计算按类别f-分数的平均值。分类报告中给出的就是这个值；

3、"微"平均：计算所有类别中假正例、假反例和真正例的总数，然后利用这些计数来计算准确率、召回率和f-分数。

如果对每个样本等同看待，那么推荐使用"微"平均分数，如果对每个类别等同看待，那么使用"宏"平均分数：

python 复制代码

print('微平均f1分数：{:.3f}'.format(f1_score(y_test,pred,average='micro')))
print('宏平均f1分数：{:.3f}'.format(f1_score(y_test,pred,average='macro')))