打卡Day9
- 1.151.翻转字符串里的单词
- 2.右旋字符串
- [3.28. 实现 strStr()](#3.28. 实现 strStr())
- 4.459.重复的子字符串
1.151.翻转字符串里的单词
题目链接:翻转字符串里的单词
文档讲解: 代码随想录
思路:首先,移除多余的空格;然后,将整体字符串反转;最后,将单个单词反转。
在python中,字符串是不可变类型,因此,需要将其转变成list,再使用join函数将其再转变为字符串,因此,空间复杂度不是O(1)。
python
class Solution(object):
def reverseWords(self, s):
"""
:type s: str
:rtype: str
"""
#删除前后空白
s.strip()
#将整个字符串反转
s = s[::-1]
#将单词反转
s = " ".join(word[::-1] for word in s.split())
return s
python
class Solution(object):
def reverseWords(self, s):
"""
:type s: str
:rtype: str
"""
word = s.split()
left, right = 0, len(word) - 1
while left < right:
word[left], word[right] = word[right], word[left]
left += 1
right -= 1
return ' '.join(word)
python
class Solution(object):
def reverseWords(self, s):
"""
:type s: str
:rtype: str
"""
word = s.split()
word = word[::-1]
return ' '.join(word) 面试的时候最好还是不要用内置的split函数,所以我在力扣的解答里找到了一个不用split函数的答案。
思路:首先,删掉首位空格。然后,需要定义一个新列表来存储从s中倒序取到的单词。接着,定义两个指针 i 和 j,初始位置在s的末尾,左移 i 直至 s[i] 不为空格,此时需要存储的单词就是 s[i+1:j+1];继续左移 i 以寻找下一个单词,当遍历到 s[i] 不为空格时,令 j=i,重复左移 i。最后,使用 join 函数拼接字符串。
python
class Solution(object):
def reverseWords(self, s):
"""
:type s: str
:rtype: str
"""
#删掉首尾空格
s = s.strip()
i = j = len(s) - 1
res = []
while i >= 0:
while i >= 0 and s[i] != ' ':
i -= 1
res.append(s[i + 1: j + 1])
while s[i] == ' ':
i -= 1
j = i
return ' '.join(res)2.右旋字符串
题目链接:右旋字符串
文档讲解: 代码随想录
python
k = int(input())
s = input()
s = s[-k:] + s[:-k]
print(s)
python
k = int(input())
s = input()
s = s[lens(s) - k:] + s[:len(s) - k]
print(s)卡码网是需要有输入有输出的。
3.28. 实现 strStr()
题目链接:实现 strStr()
文档讲解: 代码随想录
暴力解法:
python
class Solution(object):
def strStr(self, haystack, needle):
"""
:type haystack: str
:type needle: str
:rtype: int
"""
m, n = len(haystack), len(needle)
for i in range(m):
if haystack[i:i+n] == needle:
return i
return -1KMP算法用来判断一个字符串是否出现在另一个字符串中。
前缀表不减一
python
class Solution:
def getNext(self, next: list[int], s: str) -> None:
j = 0
next[0] = 0
for i in range(1, len(s)):
while j > 0 and s[i] != s[j]:
j = next[j - 1]
if s[i] == s[j]:
j += 1
next[i] = j
def strStr(self, haystack: str, needle: str) -> int:
if len(needle) == 0:
return 0
next = [0] * len(needle)
self.getNext(next, needle)
j = 0
for i in range(len(haystack)):
while j > 0 and haystack[i] != needle[j]:
j = next[j - 1]
if haystack[i] == needle[j]:
j += 1
if j == len(needle):
return i - len(needle) + 1
return -1前缀表减一
python
class Solution:
def getNext(self, next: list[int], s: str) -> None:
j = -1
next[0] = -1
for i in range(1, len(s)):
while j >= 0 and s[i] != s[j + 1]:
j = next[j]
if s[i] == s[j + 1]:
j += 1
next[i] = j
def strStr(self, haystack: str, needle: str) -> int:
if len(needle) == 0:
return 0
next = [0] * len(needle)
self.getNext(next, needle)
j = -1
for i in range(len(haystack)):
while j > 0 and haystack[i] != needle[j + 1]:
j = next[j]
if haystack[i] == needle[j + 1]:
j += 1
if j == len(needle) - 1:
return i - len(needle) + 1
return -14.459.重复的子字符串
题目链接:重复的子字符串
文档讲解: 代码随想录
除了暴力求解外,还有两种解法。
(1)移动匹配,字符串是由重复的子字符串组成,则s+s,一定还存在一个s。在判断s+s拼接的字符串中是否出现一个s的时候,要刨除s+s的首字符和尾字符,以避免在s+s中搜索出原来的s。
.find(s) 是字符串方法,用于查找子字符串 s 在字符串 ss 中的第一次出现的位置索引。如果找到了,则返回该子字符串第一次出现的索引值;如果没有找到,则返回 -1。
python
class Solution(object):
def repeatedSubstringPattern(self, s):
"""
:type s: str
:rtype: bool
"""
if len(s) <= 1:
return False
ss = s[1:] + s[:-1]
return ss.find(s) != -1(2)KMP算法
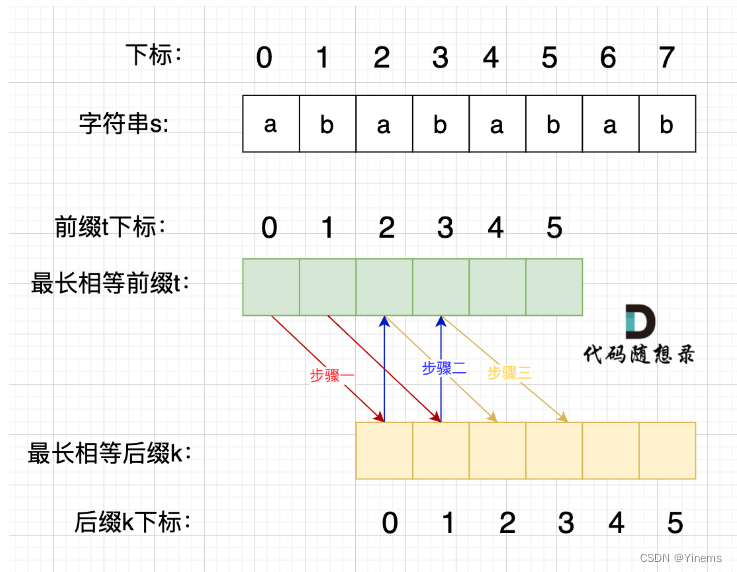
在由重复子串组成的字符串中,最长相等前后缀不包含的子串就是最小重复子串。
t0 = k0, t1 = k1,因此 t01 = k01。
t2 = k0, t3 = k1,因此 t23 = k01。
t2 = k2, t3 = k3,因此 t23 = k23.
循环往下,可以证明。
判断方法:数组长度减去最长相同前后缀的长度相当于是第一个周期的长度,也就是一个周期的长度,如果这个周期可以被整除,就说明整个数组就是这个周期的循环。
假设 s 是由 n 个重复子字符串 x 构成的,s 的最长相等前后缀一定不包含 s 本身,则一定是由 n-1 个 x 构成的。最长最长相等前后缀的长度为 next[len(s) - 1] + 1,则一个周期的长度为 len(s) - (next[len(s) - 1] + 1)。
python
#前缀表减一
class Solution:
def repeatedSubstringPattern(self, s: str) -> bool:
if len(s) == 0:
return False
net = [0] * len(s)
self.getNext(net, s)
if net[- 1] != -1 and len(s) % (len(s) - (net[- 1] + 1)) == 0:
return True
return False
def getNext(self, net: list[int], s:str) -> None:
j = -1
net[0] = -1
for i in range(1, len(s)):
while j >= 0 and s[j + 1] != s[i]:
j = net[j]
if s[j + 1] == s[i]:
j += 1
net[i] = j
python
#前缀表不减一
class Solution:
def repeatedSubstringPattern(self, s: str) -> bool:
if len(s) == 0:
return False
net = [0] * len(s)
self.getNext(net, s)
if net[- 1] != 0 and len(s) % (len(s) - (net[- 1])) == 0:
return True
return False
def getNext(self, net: list[int], s:str) -> None:
j = 0
net[0] = 0
for i in range(1, len(s)):
while j > 0 and s[j] != s[i]:
j = net[j - 1]
if s[j] == s[i]:
j += 1
net[i] = j