文章目录
一、部分题目
2018年高教社杯全国大学生数学建模竞赛题目
A题 高压油管的压力控制
燃油进入和喷出高压油管是许多燃油发动机工作的基础,图 1 给出了某高压 燃油系统的工作原理,燃油经过高压油泵从 A 处进入高压油管,再由喷口 B 喷 出。燃油进入和喷出的间歇性工作过程会导致高压油管内压力的变化,使得所喷 出的燃油量出现偏差,从而影响发动机的工作效率。
请建立数学模型解决以下问题
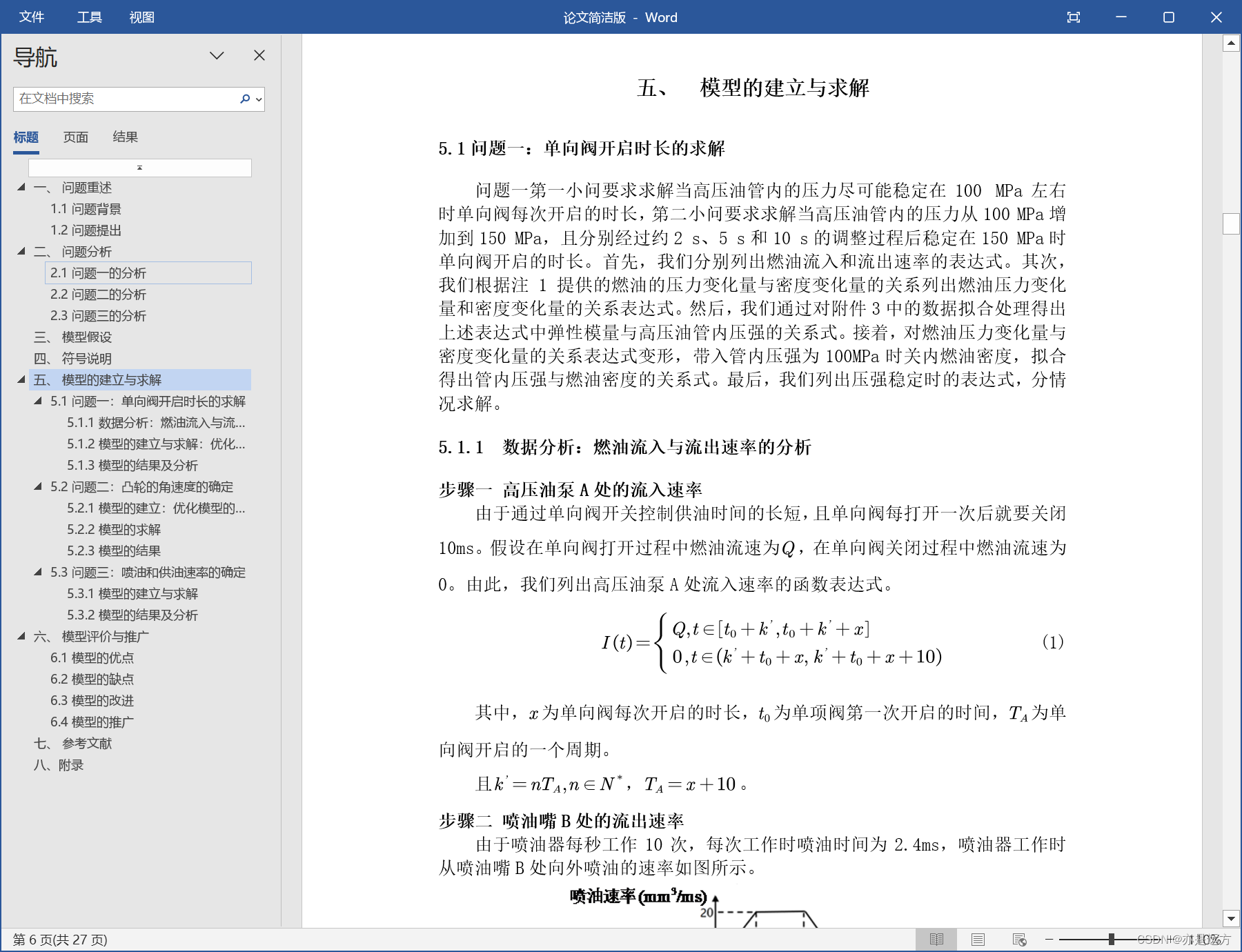
问题1 某型号高压油管的内腔长度为 500mm,内直径为 10mm,供油入口 A 处小孔的直径为 1.4mm,通过单向阀开关控制供油时间的长短,单向阀每打开 一次后就要关闭 10ms。喷油器每秒工作 10 次,每次工作时喷油时间为 2.4ms, 喷油器工作时从喷油嘴 B 处向外喷油的速率如图 2 所示。高压油泵在入口 A 处 提供的压力恒为 160 MPa,高压油管内的初始压力为 100 MPa。如果要将高压油 管内的压力尽可能稳定在 100 MPa 左右,如何设置单向阀每次开启的时长?如 果要将高压油管内的压力从 100 MPa 增加到 150 MPa,且分别经过约 2 s、5 s 和 10 s 的调整过程后稳定在 150 MPa,单向阀开启的时长应如何调整?
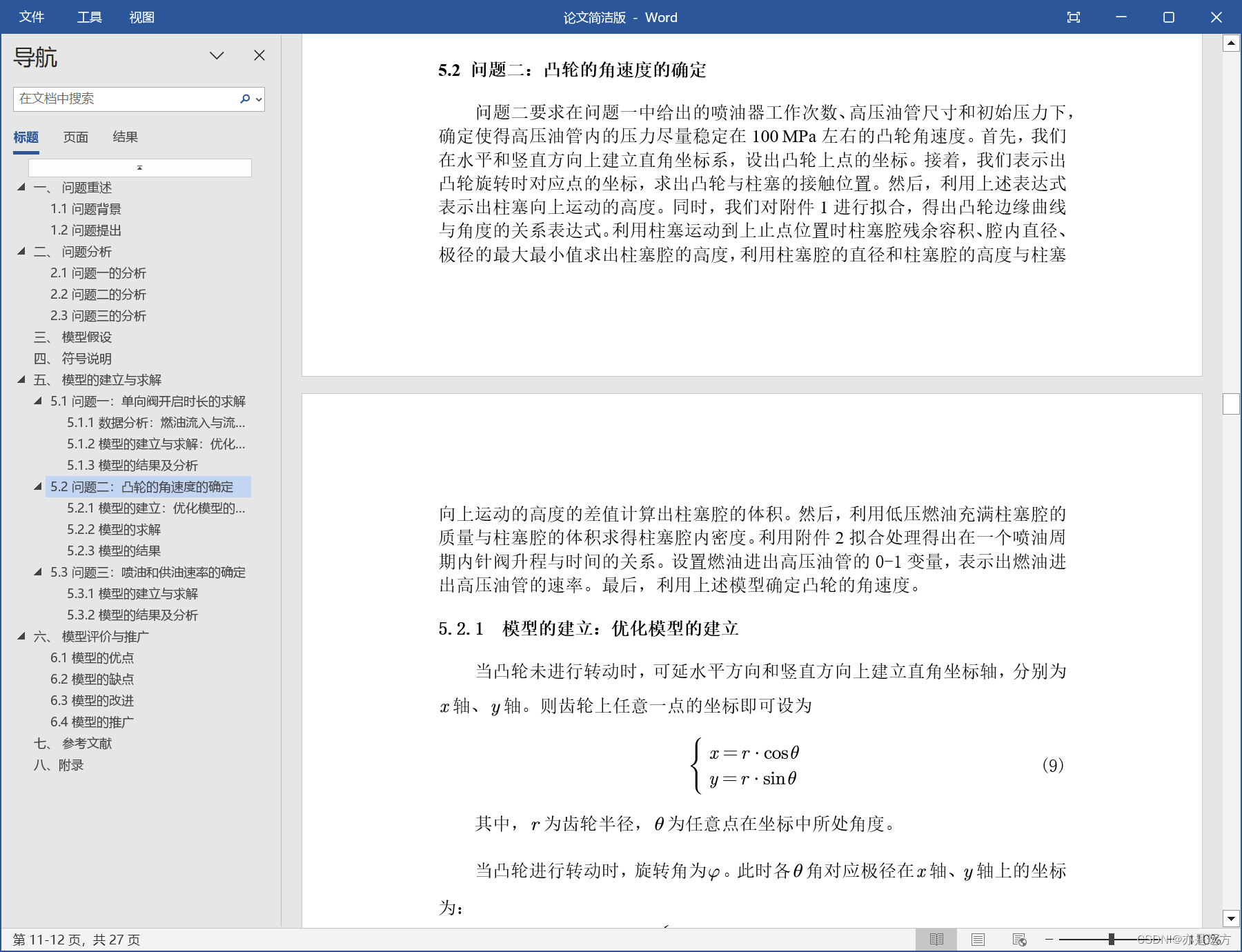
问题2 在实际工作过程中,高压油管A处的燃油来自高压油泵的柱塞腔出口, 喷油由喷油嘴的针阀控制。高压油泵柱塞的压油过程如图3所示,凸轮驱动柱塞 上下运动,凸轮边缘曲线与角度的关系见附件1。柱塞向上运动时压缩柱塞腔内 的燃油,当柱塞腔内的压力大于高压油管内的压力时,柱塞腔与高压油管连接的 单向阀开启,燃油进入高压油管内。柱塞腔内直径为5mm,柱塞运动到上止点位 置时,柱塞腔残余容积为20mm3。柱塞运动到下止点时,低压燃油会充满柱塞腔 (包括残余容积),低压燃油的压力为0.5 MPa。喷油器喷嘴结构如图4所示,针 阀直径为2.5mm、密封座是半角为9°的圆锥,最下端喷孔的直径为1.4mm。针阀 升程为0时,针阀关闭;针阀升程大于0时,针阀开启,燃油向喷孔流动,通过喷 孔喷出。在一个喷油周期内针阀升程与时间的关系由附件2给出。在问题1中给出 的喷油器工作次数、高压油管尺寸和初始压力下,确定凸轮的角速度,使得高压 油管内的压力尽量稳定在100 MPa左
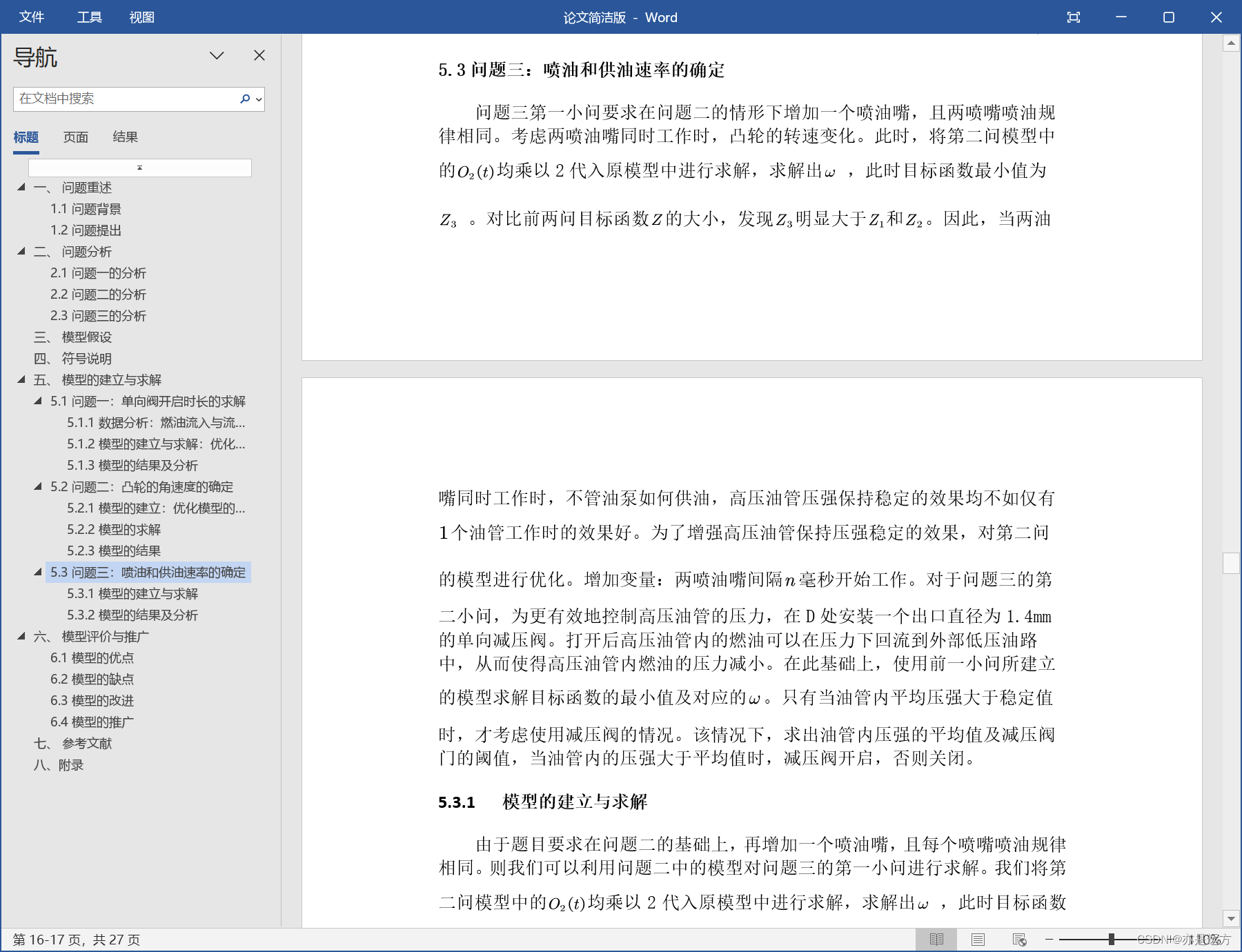
问题3在问题2的基础上,再增加一个喷油嘴,每个喷嘴喷油规律相同,喷 油和供油策略应如何调整?为了更有效地控制高压油管的压力,现计划在D处安 装一个单向减压阀(图5)。单向减压阀出口为直径为1.4mm的圆,打开后高压油 管内的燃油可以在压力下回流到外部低压油路中,从而使得高压油管内燃油的压 力减小。请给出高压油泵和减压阀的控制方案。
二、部分论文
三、部分源代码
问题1
(1)绘制弹性模量与压力函数图
c
x=xlsread('附件3-弹性模量与压力.xlsx','Sheet1','A2:A402');
y=xlsread('附件3-弹性模量与压力.xlsx','Sheet1','B2:B402');
figure('color','w');
scatter(x,y,'ro');
hold on;
y2=0.0001*x.^3-0.001082*x.^2+5.474*x+1532;
scatter(x,y2,'g.');
axis([0,205,1500,3400]);
xlabel('压力(MPa)');
ylabel('弹性模量(MPa)');
legend('原数据图像(加粗)','拟合函数图像');
box off;(2)求最优单次开阀时间
c
clear,clc;
C=0.85;
A=0.49*pi;%小孔面积
V=12500*pi;%油管体积
tstep=0.02;%确定步长
z=zeros(1,length(0.01:0.01:5));%储存稳定目标值
pos1=1; %z的下标
%遍历法探索可能解
for topen=0.01:0.01:5
Pyb=160; %油泵压力
Pyg=100; %油管压力
rouyb=0.8725; %油泵油密度
rouyg=0.85; %油管油密度
tclose=10; %闭阀时间
myg=rouyg*V; %起始油管油质量
P=zeros(1,length(0:tstep:2000)); %储存油管压力值
pos2=1; %P的下标
%迭代时间
for t=0:tstep:2000
%计算体积变化
Qin=State(t,topen,tclose)*C*A*sqrt(2*(Pyb-Pyg)/rouyb)*tstep;
Qout=py(t)*tstep;
myg=myg+(Qin-Qout)*rouyg; %计算油管油质量
rouyg=myg/V; %更新油管油密度
Pyg=y(rouyg); %更新油管油压力
P(pos2)=Pyg;
pos2=pos2+1;
end
z(pos1)=sum((100-Pyg).^2);
pos1=pos1+1;
end
[i,j]=min(z);
topen=j/100;
%密度转化为压力
function P=y(x)
P=17284.0015*x^2-27111.3456*x+10656.1125;
end
%单向阀状态
function flag=State(t,topen,tclose)
%topen为开阀时间,tclose为关阀时间
T=topen+tclose;%总周期
mt=mod(t,T); %放入第一周期
if mt<=topen %开阀
flag=1;
else
flag=0; %闭阀
end
end
%输入时间,输出喷油速率
function v=py(t)
nt=mod(t,100);%放入第一周期
if nt<=0.2
v=100*nt;
elseif nt<=2.2
v=20;
elseif nt<=2.4
v=240-100*nt;
else
v=0;
end
end问题二
(1)极径与极角关系
c
a=xlsread('附件3-弹性模量与压力.xlsx','Sheet1','A2:A629');
r=xlsread('附件3-弹性模量与压力.xlsx','Sheet1','B2:B629');
y=-0.06315*a.^4+0.7934*a.^3-2.647*a.^2+0.9696*a+7.09;
figure('color','w');
plot(a,r,'r:','Linewidth',3);
hold on;
plot(a,y,'b-');
axis([0,6.27,2,8]);
xlabel('极角(rad)');
ylabel('极径(mm)');
box off;(2)求最优凸轮角速度
c
clear,clc;
C=0.85;
A=0.49*pi;%小孔面积
V=12500*pi;%油管体积
d1=2.5;
d3=1.4;
s1=0.25*pi*d1^2; %针阀面积
s3=0.25*pi*d3^2; %圆锥缺口圆环面积
L=0.5*d1/tan(pi/20); %初始针阀底端到圆锥缺口高度
tstep=0.02;%确定步长
z=zeros(1,length(0.0001:0.0001:0.05));%储存稳定目标值
pos1=1; %z的下标
%遍历法探索可能解
for w=0.0001:0.0001:0.05
Pyb=0.5; %油泵压力
Pyg=100; %油管压力
rouyg=0.85; %油管油密度
myg=rouyg*V; %起始油管油质量
P=zeros(1,length(0:tstep:2000)); %储存油管压力值
pos2=1; %P的下标
%迭代时间
for t=0:tstep:2000
rouyb=0.7919*17.896/(17.896-H(w,t));
Pyb=y(rouyb);%此时油泵油压力
r2=(L+h(t))*tan(pi/20);
s2=pi*r2^2; %针阀底端与圆锥相切处圆环的面积
B=min(s2-s1,s3); %流出面积
%计算体积变化
Qin=State1(Pyb,Pyg)*C*A*sqrt(2*(Pyb-Pyg)/rouyb)*tstep;
Qout=State2(t)*C*B*sqrt(2*(Pyg-0.1)/Y(Pyg))*tstep;
myg=myg+(Qin-Qout)*rouyg; %计算油管油质量
rouyg=myg/V; %更新油管油密度
Pyg=y(rouyg); %更新油管油压力
P(pos2)=Pyg;
pos2=pos2+1;
end
z(1,pos1)=sum((100-P).^2);
pos1=pos1+1;
end
[i,j]=min(z);
mubiao=j/10000;
%密度转化为压力
function P=y(x)
P=17284.0015*x^2-27111.3456*x+10656.1125;
end
%压力转化为密度
function rou=Y(x1)
rou=-1.68e-6*x1^2+0.0006374*x1+0.7916;
end
%极角化极径
function jj=r(a)
jj=-0.06315*a^4+0.7934*a^3-2.647*a^2+0.9696*a+7.09;
end
%单向阀状态
function flag1=State1(Pyb,Pyg)
if Pyb>Pyg %开阀
flag1=1;
else
flag1=0; %闭阀
end
end
%喷口状态
function flag2=State2(t)
nt=mod(t,100);%放入第一周期
if nt<2.45 %喷出
flag2=1;
else
flag2=0; %不喷出
end
end
%计算活塞上升高度
function HT=H(w,t)
u=zeros(1,length(0:0.1:2*pi));
pos3=1;
for a=0:0.1:2*pi
u(1,pos3)=r(a)*sin(w*t+a);
pos3=pos3+1;
end
HT=max(u)-2.143;
end
%针阀上升高度
function hp=h(t)
kt=mod(t,100);%放入一个周期
if kt<0.45
hp=2.016*exp(-((t-0.4551)/0.1661)^2);
elseif kt<=2
hp=2;
elseif kt<2.45
hp=2.016*exp(-((-(t-2.45)-0.4551)/0.1661)^2);
else
hp=0;
end
end