1.离散型分布
1.1 两点分布(伯努利分布/贝努利分布/0-1分布)
称随机变量 \(X\) 服从参数为 \(p\) 的伯努利分布,如果它分别以概率 \(p\) 和 \(1-p\) 取 1 和 0 为值。
\[P(X=k)=p^k(1-p)^{1-k}, \quad k=0,1\\ X\sim B(1,p)\\ E(X)=p\\ D(X)=p(1-p) \]
1.2 二项分布
n次独立的伯努利试验。如果事件发生的概率是 \(p\),n次独立重复试验中发生k次的概率是(有放回抽样)
\[P(X=k)=\mathrm C_n^k p^k(1-p)^{n-k},\quad k=0,1,...,n\\ X\sim B(n,p)\\ E(X)=np\\ D(X)=np(1-p) \]
有 \(n\) 件产品,其中 \(m\) 件次品 (\(m<n\)),从中不放回地任意抽取 \(k\) 件产品和有放回地任意抽取 \(k\) 件产品,在这两种抽取方法中每次抽出次品的概率相同,都为 \(\frac{m}{n}\),抽得次品数的期望值也相同,都为 \(k\frac{m}{n}\),但抽到的次品数的分布列不同,方差不同(超几何分布与二项分布)
关于为什么不放回抽样,每次抽到次品的概率都是 \(\frac{m}{n}\),因为不放回抽样,每次抽样,都是与前些次的抽样相关的。
第一次抽样,抽中次品的概率为 \(\frac{m}{n}\),
第二次抽样,抽中次品的概率为 \(\frac{m}{n}\times\frac{m-1}{n-1}+\frac{n-m}{n}\times\frac{m}{n-1}=\frac{m}{n}\),
第三次抽样,抽中次品的概率为
\(\frac{m}{n}\times\frac{m-1}{n-1}\times\frac{m-2}{n-2}+\frac{m}{n}\times\frac{n-m}{n-1}\times\frac{m-1}{n-2}+\frac{n-m}{n}\times\frac{m}{n-1}\times\frac{m-1}{n-2}+\frac{n-m}{n}\times\frac{n-m-1}{n-1}\times\frac{m}{n-2}\),经过计算可得仍为 \(\frac{m}{n}\)
1.3 几何分布
在n次伯努利试验中,试验k次才第一次成功的概率。几何分布是帕斯卡分布当 \(r=1\) 时的特例
\[P(X=k)=(1-p)^{k-1}p,\quad k=1,2,...\\ X \sim GE(p)\\ E(X)=\frac{1}{p}\\ D(X)=\frac{1-p}{p^2} \]
例:某产品的合格率为0.05,则首次查到不合格品的检查次数 \(X\sim GE(0.05)\)
1.4 帕斯卡分布(负二项分布)
在重复独立的伯努利试验中,设每次试验成功的概率为 \(p\),若将试验进行到出现 \(r\) (\(r\) 为常数) 次成功为止,以随机变量 \(X\) 表示所需试验次数,
\[P(X=k)=\mathrm C_{k-1}^{r-1}p^r(1-p)^{k-r}, \quad k=r,r+1,...\\ E(X)=\frac{r}{p} \]
(当 \(r\) 是整数时,负二项分布又称帕斯卡分布)
1.5 超几何分布
从 N 个物件中抽出 n 个物件,成功抽出指定种类的物件的次数(不放回抽样)。
\(X\sim H(N,M,n)\)
产品抽样检查中,假定在 N 件产品中有 M 件不合格品,即不合格率为 \(\frac{M}{N}\),在产品中随机抽 n 件进行检查,发现 k 件不合格品的概率为
\[P(X=k)=\frac{\mathrm C_M^k \mathrm C_{N-M}^{n-k}}{\mathrm C_N^n},\quad k=0,1,...,min\{n,M\}\\ E(X)=\frac{nM}{N}\\ D(X)=n\frac{M}{N}(1-\frac{M}{N})\frac{N-m}{N-1} \]
1.6 泊松分布
泊松分布适用于描述单位时间内随机事件发生的次数,泊松分布的参数 \(\lambda\) 是单位时间内随机事件的平均发生次数。
\[P(X=k)=\frac{\lambda^k}{k!}e^{-\lambda}, \quad k=0,1,...\\ E(X)=\lambda\\ D(X)=\lambda \]
特征函数:\(\Psi(t)=\exp\{\lambda(e^{it}-1)\}\)
2.连续型分布
2.1 均匀分布 \(U(a,b)\)
密度函数:
\[f(x)=\left\{ \begin{aligned} &\frac{1}{b-a}&,&\quad a<x<b \\ &0&,&\quad 其他 \end{aligned} \right. \]
分布函数:
\[F(x)=\left\{ \begin{aligned} &0&,&\quad x<a \\ &\frac{x-a}{b-a}&,&\quad a\leq x < b\\ &1&,&\quad x\geq b \end{aligned} \right. \]
期望和方差:
\[E(X)=\frac{a+b}{2}\\ D(X)=\frac{(b-a)^2}{12} \]
2.2 指数分布 \(E(\lambda)\)
\[f(x)=\left\{ \begin{aligned} &\lambda e^{-\lambda x} &,&\quad x>0 \\ &0&,&\quad 其他 \end{aligned} \right. \]
\[F(x)=\left\{ \begin{aligned} &0&,&\quad x<0\\ &1-e^{-\lambda x} &,&\quad x\geq0 \\ \end{aligned} \right. \]
\[E(X)=\frac 1\lambda\\ D(X)=\frac {1}{\lambda^2} \]
2.3 正态分布 \(N(\mu, \sigma^2)\)
\[f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}},\quad -\infty <x<+\infty\\ F(x)=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^x e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt\\ \]
\[E(X)=\mu\\ D(X)=\sigma^2 \]
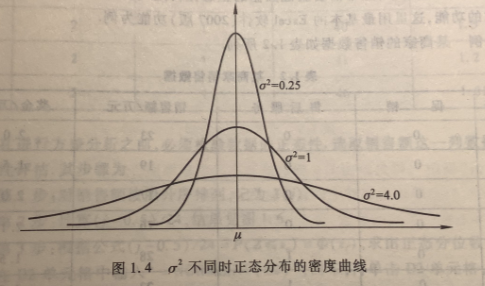
一般来说,正态分布的密度曲线是以为中心,在 \(\mu\) 的两侧呈对称的形状,曲线的形状像一个钟的剖面,故称为钟形曲线。 \(\sigma\) 越大,密度曲线的峰度越低; \(\sigma\) 越小,密度曲线的峰度越高。无论参数 \(\mu\) 和 \(\sigma\) 取何值,密度曲线下所覆盖的面积均于 1。 正态分布的密度曲线见图 1.4 。
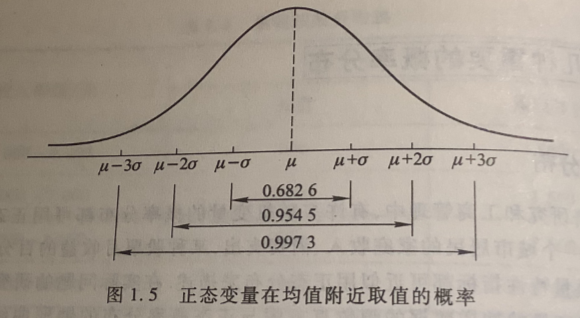
正态分布曲线下,位于\(\mu\pm \sigma, \mu\pm 2\sigma, \mu\pm 3\sigma\) 之间的面积分别约占总面积的 68.26%,95.45%, 99.73%, 如 图 1.5 所示 。
当总体概率分布为正态分布时,作为从中抽出的样本,其统计量的样本概率分布有卡方分布,t分布,F分布等。因此正态分布成为计量经济学乃至统计学中最重要的概念之一。
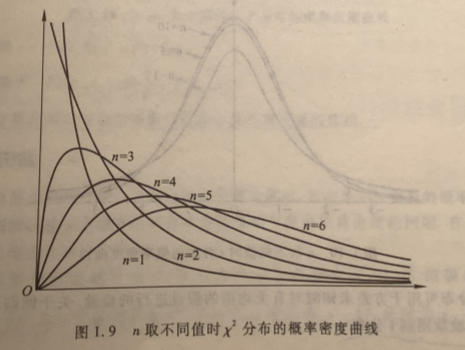
2.4 \(\chi^2\)分布
如果从标准正态分布 \(N(0,1)\) 的总体中得到 n 个独立的随机变量分别为 \(X_1, X_2, ..., X_n\),则由 \(\sum_{i=1}^n X_i^2\) 得到的分布称作自由度为 n 的 \(\chi^2\) 分布,记为 \(X\sim \chi^2(n)\).
期望和方差:
\[E(X)=n\\ D(X)=2n \]
\(\chi^2\) 分布的加法定理. 设 \(X_1, X_2, ..., X_k\) 是相互独立的随机变量,且 \(X_i\sim \chi^2(n_i), i=1,2,...,k\),则
\[\sum_{i=1}^k X_i \sim \chi^2(n_1+n_2+...+n_k). \]
\(\chi^2\)分布与 \(N(0,1)\) 分布之间有如下关系:
设 \(X_1, X_2, ..., X_n\) 是相互独立的随机变量,并且 \(X_i\sim N(0,1), i=1,2,...,n\),则
\[\sum_{i=1}^n X_i^2\sim \chi^2(n). \]
2.5 t分布
设随机变量 \(X\sim N(0,1), Y\sim \chi^2(n)\),X 与 Y 相互独立,则随机变量
\[t=\frac{X}{\sqrt{Y/n}} \]
遵从自由度为n的t分布,记为 \(t=\frac{X}{\sqrt{Y/n}}\sim t(n)\).
期望和方差:
当n>2时,\(E(t)=0, D(t)=\frac{n}{n-2}\).
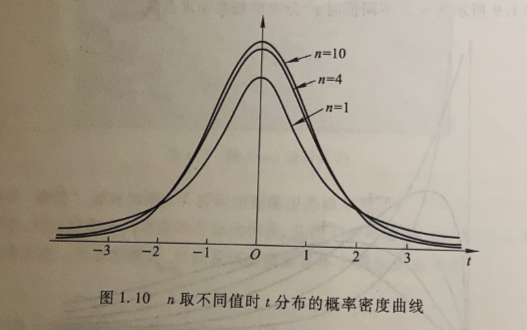
当n<30时,t分布的分散程度比标准正态分布大,密度函数曲线比较平缓,随着n的增大,t分布逐渐接近标准正态分布;当 \(n\rightarrow\infty\)时,t分布渐进标准正态分布
t分布可用于方差未知时对有关均值的假设进行检验。关于回归系数的显著性检验就用到 t分布。
2.6 F分布
设随机变量 \(X\sim \chi^2(n_1), Y\sim \chi^2(n_2)\),且X与Y相互独立,则称随机变量
\[F=\frac{X/n_1}{Y/n_2} \]
遵从自由度为 \((n_1,n_2)\) 的F分布,记作 \(F\sim F(n_1,n2)\).
F分布的形状为正偏态分布,随着 \(n_1,n_2\) 的增大,其概率密度曲线的偏斜度虽有所减缓却仍保持偏态分布,并不以正态分布为其极限分布形式。
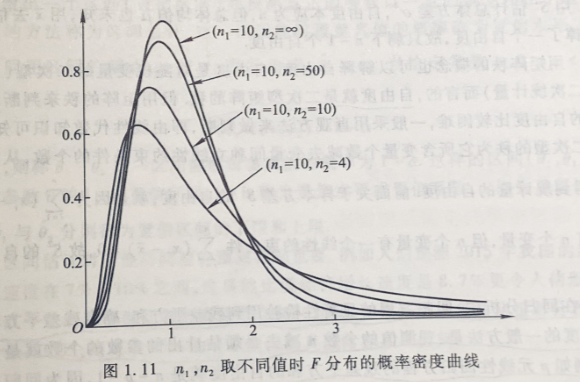
如果 \(t\sim t(n)\),则 \(t^2\sim F(1,n)\);
如果 \(F\sim F(n_1,n_2)\),则 \(\frac1F \sim F(n_2, n_1)\).
F分布在回归方程的显著性检验中具有重要作用