这篇文章是 2022 ECCV 的一篇文章,是旷视科技的一篇文章,针对图像恢复任务各种网络结构进行了梳理,最后总结出一种非常简单却高效的网络结构,这个网络结构甚至不需要非线性激活函数。
文章一开始就提到,虽然在图像复原领域,可以看到非常明显的进步和提升,但是这些算法框架的复杂性也随之增加。这篇文章重新思考了算法框架的设计,提出了一种非常简单的基线算法框架,这个基线算法框架不仅效果上可以超越当前的一些 SOTA 方法,而且运算效率也非常高。文章为了进一步简化这个基线模型,甚至将其中的非线性激活函数,比如 Sigmoid,ReLU,GELU,Softmax 等都可以等效替换成简单的线性相乘,最终文章提出了一个非常简单高效的基线算法框架,称为 NAFNet,全称叫 Nonlinear Activation Free Network,这个算法框架在多个图像复原任务上都以极低的运算代价取得与 SOTA 相当甚至超越 SOTA 的效果。如图 1 所示:
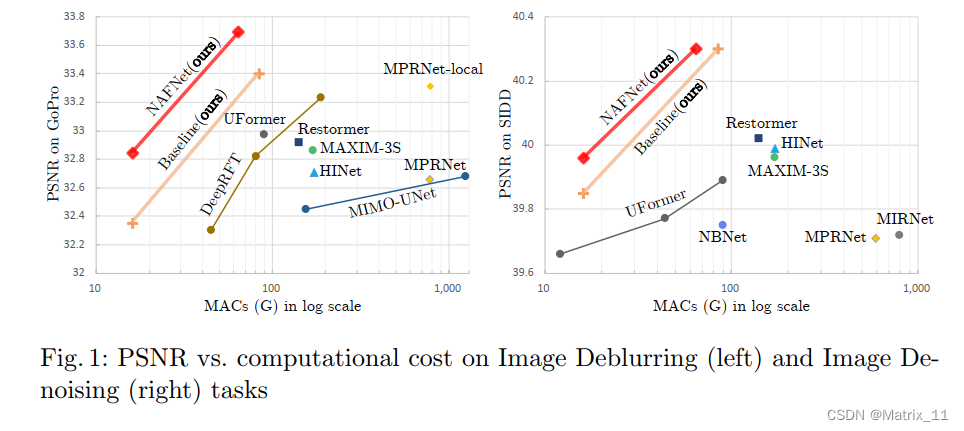
- 图1
图像恢复任务就是将一张退化的图像(比如模糊,有噪)恢复成清晰图像,目前这类图像恢复任务基本都是基于深度学习的方法在做了,这类方法也取得了越来越好的复原效果,指标也越刷越高,绝大多数的深度学习方法,都是基于一个经典的架构,UNet,将多个 blocks 叠加成一个 U 型,中间还会带着 skip 的连接,在这个经典架构的基础上,衍生出很多变体,这些变体带来了处理效果的提升,也导致了模型的复杂度随之增加,这篇文章将模型的复杂度分为两种,一种是 block 之间的复杂度,一种是 block 内的复杂度。
-
Inter-block Complexity,一般都是多阶段的网络结构,后面阶段的网络结构会对前面阶段的输出进行 refine,每个阶段都是一个 U 型的结构,这种多阶段的设计,是想把一个困难的任务,拆分成几个简单的子任务。
-
Intra-block Complexity,有很多工作会聚焦在 block 之间的设计,文章作者也列举了一些例子。比如有的工作会将 attention 机制进行简化,用 channel attention 代替常规的 spatial attention。此外,gated liner units 和 depthwise 卷积也比较常见。还有的工作是设计了基于窗口的多头注意力机制。不过本文作者想说明的是,提升系统复杂度不是唯一的提升性能的方法,有的时候一些简单的设计也能取得 SOTA 的表现。
Build A Simple Baseline
接下来,文章开始介绍,如何构建一个足够简单的基线结构,文章作者构建的原则就是奥卡姆剃刀原则:如无必要,勿增实体 ,不过文章也说了,必要性的判断依据是实验经验。文章将模型的运算量限制在 16GMACs,对应的输入图像大小为 256 x 256。然后主要评估的图像复原任务是降噪和去模糊。文章中用到的网络结构,是最简单的 U 型结构,如图 2C 所示
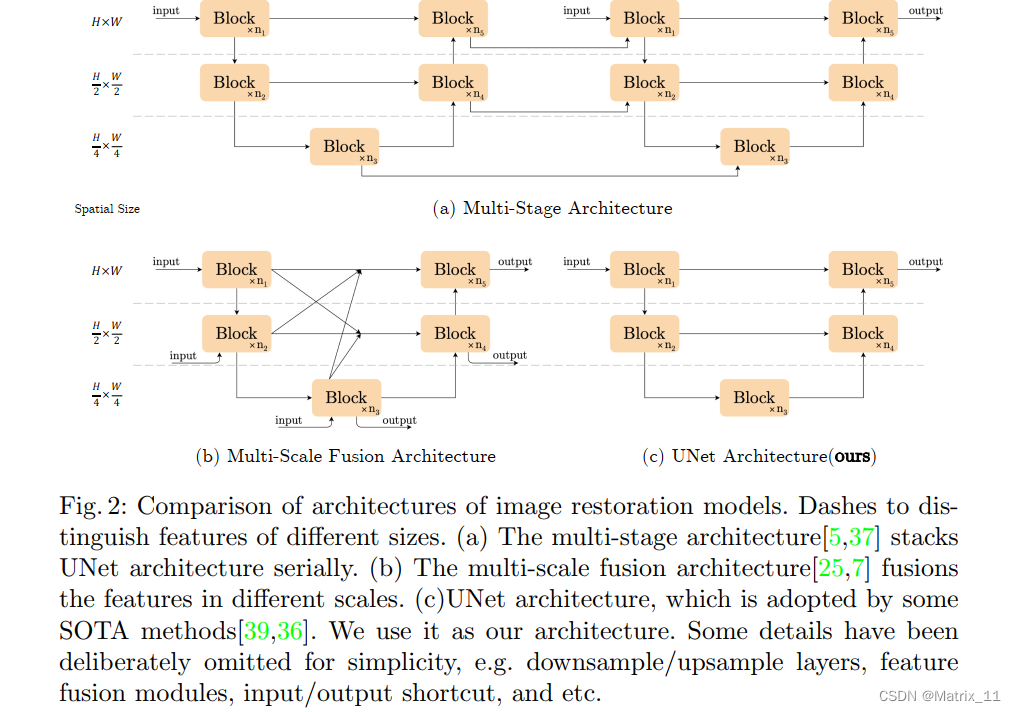
- 图 2
神经网络一般都是由 block 叠加而成的,文章用最简单的 residual block 构成基础模型 PlainNet,如图 3b 所示;
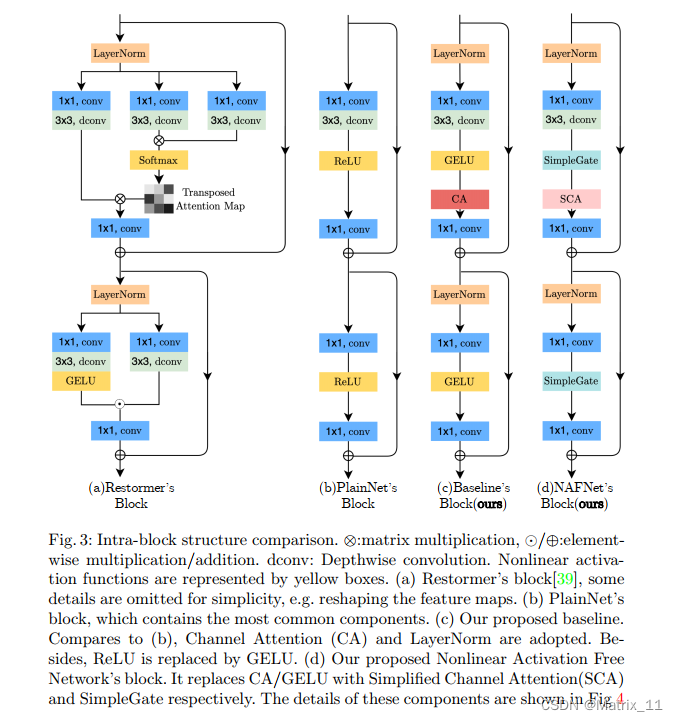
- 图 3
文章接下来对 PlainNet 中的主要模块进行了讨论,包括 Normalization, Activation 以及 Attention 机制。
Normalization
现在已经有好几种不同的 Normalization 的方法,包括 batch Normalization, instance Normalization, layer Normalization 等,不同的任务,不同的网络结构,这些 Normalization 的方法发挥的作用可能也不一样。所以文章作者经过比较,最后采用了 layer Normalization 这种方法。
Activation
对于激活函数,relu 是大家经常用的一种激活函数,不过,现在也逐渐发展出来了一些其它的激活函数类型,文章提到了 GELU,实验证明,用 GELU 比用 gelu 的效果要好:
Attention
随着 transformer 结构在 CV 领域的逐渐盛行,attention 机制也变得越来越常用,文章中也用到了 attention 机制,不过与原始的 transformer 中的 attention 机制不同,文章中用到的是 channel attention,而且是经过进一步简化的 channel attention,具体结构如图 4a 所示:
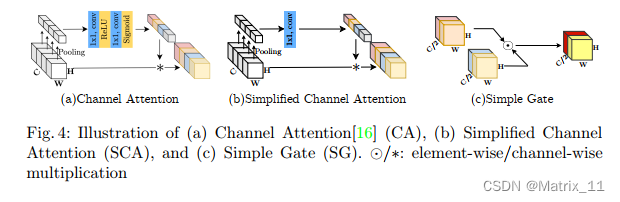
- 图 4
文章后面还会对 4a 的结构做进一步的简化。
Nonlinear Activation Free Network
上面的 PlainNet 运算复杂度相比之前的一些结构,已经降低了很多,但是依然可以取得 SOTA 的效果,不过文章作者并没有满足,他们认为这个网络结构可以进一步的简化,甚至可以去掉非线性激活函数,首先,文章作者分析了一些方法之后,发现 Gated Linear Units (GLU) 这个激活函数被经常用到, 所以对这个函数的性质做进一步的分析。
Gated Linear Units 的形式如下所示:
G a t e ( X , f , g , σ ) = f ( X ) ⊙ σ ( g ( X ) ) (1) Gate(\mathbf{X}, f, g, \sigma) = f(\mathbf{X}) \odot \sigma(g(\mathbf{X})) \tag{1} Gate(X,f,g,σ)=f(X)⊙σ(g(X))(1)
其中 X X X 表示 feature map, f , g f, g f,g 表示线性变换, σ \sigma σ 表示一个非线性激活函数,比如 Sigmoid, ⊙ \odot ⊙ 表示元素乘积。如果把 GLU 放入网络结构,效果可以进一步提升,但是运算复杂度也会增加,这不是文章作者想看到的,所以他们对基线网络结构中的 activation GELU 进行了改进:
G E L U ( x ) = x ϕ ( x ) (2) GELU(x) = x \phi(x) \tag{2} GELU(x)=xϕ(x)(2)
其中 ϕ \phi ϕ 表示标准正态分布的累积分布函数,一般 GELU 可以估计成如下形式:
gelu ( x ) = 0.5 x ∗ ( 1 + tanh ( 2 / π ∗ ( x + 0.044715 ∗ x 3 ) ) ) (3) \text{gelu}(x) = 0.5 x \ast (1 + \tanh(\sqrt{2/\pi} \ast (x + 0.044715 \ast x^{3} ))) \tag{3} gelu(x)=0.5x∗(1+tanh(2/π ∗(x+0.044715∗x3)))(3)
从公式 (1) 和公式 (2),可以注意到,GELU 是 GLU 一种特殊情况,如果 f , g f, g f,g 取恒等变换, σ \sigma σ 取 ϕ \phi ϕ,那 GLU 就变成 GELU 了,从这种相似性,文章作者猜测 GLU 可以看成是一类广义的激活函数,或许可以替换其它的激活函数。进一步,文章作者认为 GLU 本身就包含非线性,即使去掉 σ \sigma σ 函数, G a t e ( X ) = f ( X ) ⊙ g ( X ) Gate(\mathbf{X}) = f(\mathbf{X}) \odot g(\mathbf{X}) Gate(X)=f(X)⊙g(X) 也包含了非线性,基于这些推论,文章作者提出了一种 GLU 的简化版,直接将 feature map 在 channel 层面平分成两部分,然后再直接相乘,如图4 c 所示,这个简化后的 GLU 称为 SimpleGate,与 GELU 相比,SimpleGate 只需要简单的乘法就可以实现:
S i m p l e G a t e ( X , Y ) = X ⊙ Y (4) SimpleGate(\mathbf{X}, \mathbf{Y}) = \mathbf{X} \odot \mathbf{Y} \tag{4} SimpleGate(X,Y)=X⊙Y(4)
模块的具体结构如图 4c 所示,通过这个替换,网络的表现进一步有提升,到目前为止,网络中还剩下的非线性函数就是 channel attention 中的 Sigmoid 以及 ReLU 了。
在前面的 PlainNet 中,采用了 channel attention 的机制,如图 4a 所示,这种机制同样可以捕获到全局信息,同时保持运算的高效,它将空间信息在channel 维度先进行压缩,然后利用一个 MLP 去计算 channel attention,作为每个 feature map 的权重,再与之前的 feature map 相乘:
C A ( X ) = X ∗ σ ( W 2 max ( 0 , W 1 p o o l ( X ) ) ) (5) CA(\mathbf{X}) = \mathbf{X} \ast \sigma(W_{2} \max (0, W_{1} pool(\mathbf{X}))) \tag{5} CA(X)=X∗σ(W2max(0,W1pool(X)))(5)
其中, X \mathbf{X} X 表示 feature map,pool 表示全局平均池化操作, σ \sigma σ 表示 Sigmoid 函数, W 1 , W 2 W_1, W_2 W1,W2 表示全连接层,如果将 channel attention 的计算看成是一个函数,那么公式 (5) 可以写成:
C A ( X ) = X ∗ Φ ( X ) (6) CA(\mathbf{X}) = \mathbf{X} \ast \Phi(\mathbf{X}) \tag{6} CA(X)=X∗Φ(X)(6)
可以看到,公式 6 与公式 1 很像,受此启发,文章作者也推测 channel attention 可能也是 GLU 的一种特殊形式,或许也可以进行类似的简化,文章将 channel attention 最终简化成如下所示:
S C A ( X ) = X ∗ W p o o l ( X ) (7) SCA(\mathbf{X}) = \mathbf{X} \ast W pool(\mathbf{X}) \tag{7} SCA(X)=X∗Wpool(X)(7)
模块的具体结构如图 4b 所示,相比 4a 的结构,4b 去掉了 Sigmoid 以及 ReLU,全连接也减少了一层
基于 PlainNet, 文章将其中的 GELU 以及 channel attention 做了简化,最终得到了一个不含非线性激活函数的轻量级网络,称为 NAFNet。
文章最后给出了很多实验对比,说明 NAFNet 在保持低运算代价的同时,还能保持很好的效果指标,真有点大道至简,大巧若拙的感觉了。