特征值究竟体现了矩阵的什么特征?
简单来说就是x经过矩阵A映射后和自己平行
希尔伯特第一次提出eigenvalue,这里的eigen就是自己的 。所以eigenvalue也称作本征值
特征值和特征向量刻画了矩阵变换空间的特征
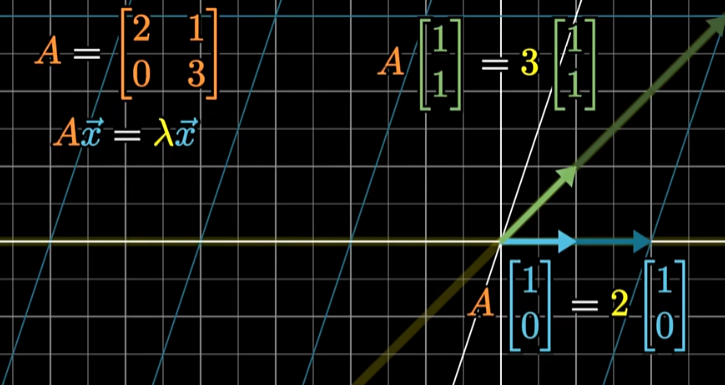
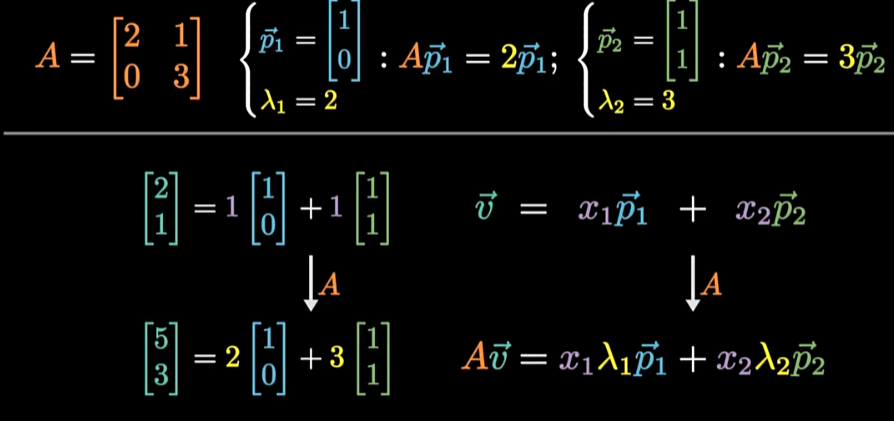
对平面上的任意向量可以如法炮制,把他在特征向量的坐标系下分解。分别在每个轴上伸缩,再用平行四边形法则加起来。就可以轻松确定任何一个向量被映射后到底在哪里。
可以说,矩阵特征向量的变化很好的描述了矩阵对空间的影响
将以上总结为3步
-
把向量分解为特征向量的线性组合
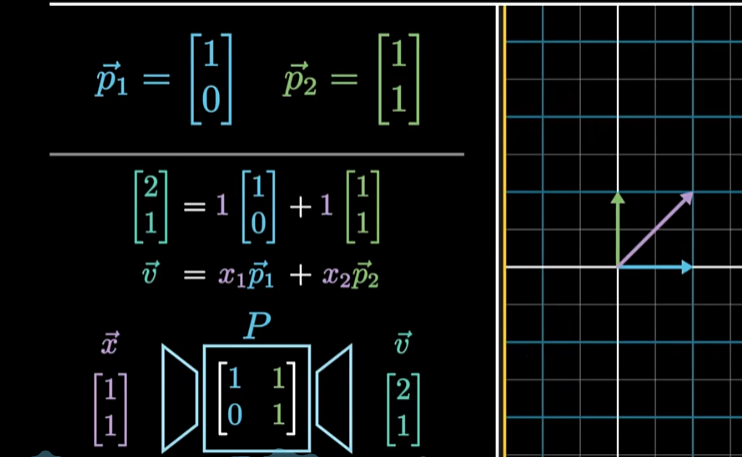
-
根据特征值分别缩放每个特征向量,两个特征值分别是2和3,所以两个系数就变成了两倍和三倍
-
重新将这些特征向量组合起来,将变换后的这些组合的系数向量使用线性映射P再变回去,就得到了原始空间的最终结果
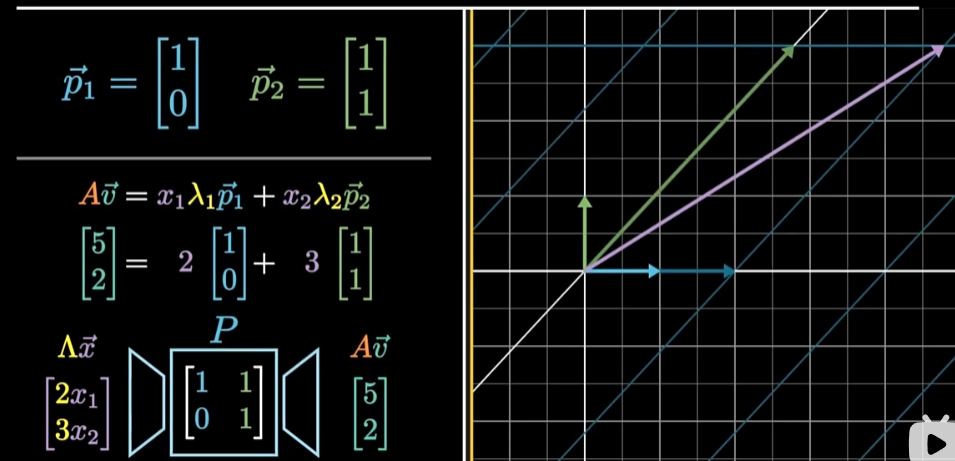
经过以上3步就得到了A作用于一个向量映射的整个过程。
我们为什么要费这么大的劲求这个分解呢?
- 计算简便
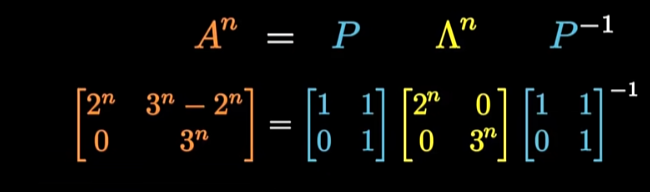
其中求特征值,利用特征多项式来求
线性空间当中几乎所有向量,经过某个线性映射的反复迭代以后,都会趋近于特征值最大的一个方向。
为什么要讲相似矩阵?
P这个矩阵承担着两个视角(默认视角和特征向量视角)之间的转换。
使用不同的视角 来观察同一个线性映射。会得到不同的矩阵,于是这些矩阵叫做相似矩阵
头尾两个矩阵,就是这两个视角的转移矩阵
这个映射具有的性质,就被所有能够用相似变换所观察到的其他矩阵所共有。在某些方向上,方向不变时,伸长的倍数是保持的。这就是为什么**所有相似矩阵,他们特征值的集合是一样的。**而特征向量不一样
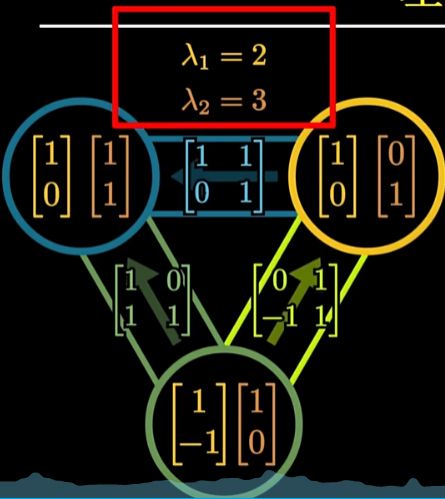
在特征向量的视角下,矩阵的迭代累乘变得特别简单,才使得我们可以用特征分解快速的计算出一个矩阵的幂次
一些结论
1.矩阵所有特征值的乘积等于行列式
2.几何重数不会超过代数重数
视频链接: