单链表 & 双指针 &
二叉树 & 心法
二叉树 & 「遍历」思维
二叉树 & 「分解问题」思维
二叉树 & 「遍历 + 分解问题」思维
二叉树的最大深度(hot100 & ACM)
题目内容
给定一个二叉树 root,输出其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
输入描述
一行包含二叉树的序列化数组,节点值之间用空格隔开,空节点用null表示。
输出描述
一个整数,表示最大深度。
样例
-
样例1:
输入:
3 9 20 null null 15 7输出:
3 -
样例2:
输入:
1 null 2输出:
2
提示
- 树中节点的数量在
[0, 10⁴]区间内。 -100 <= Node.val <= 100
二叉树 & 「后序位置」思维
写递归代码过程中发现,需要调用其他递归函数返回的结果时,就需要考虑后序遍历的思维来优化算法。
后序遍历传递可以传递子树的信息!
一旦你发现题目和子树有关,那大概率要给函数设置合理的定义和返回值,在后序位置写代码了。
652. 寻找重复的子树
- 序列化serialize操作可以记录每个节点的子树形状,将
TreeNode*序列化为string! - 要求返回结果不重复,就用
map<string, int>记录次数; - 需要用到
<string>的to_string(),以及 + 拼接字符串; - 利用序列化函数serialize函数后序位置,既先计算左右子树的序列化结果,利用后序遍历(左子树 + 右子树 + 根节点)性质,后序位置拼接左子树+ 右子树+根节点,得到当前节点的序列化结果!
- 然后检查map中 当前子树序列号结果出现的次数,如果
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
#include <string>
class Solution {
public:
unordered_map<string, int> TreeMap;
vector<TreeNode*> res;
vector<TreeNode*> findDuplicateSubtrees(TreeNode* root) {
serialize(root);
return res;
}
string serialize(TreeNode* root) {
if (root == nullptr) return "#";
// 先计算左右子树,后序位置做其他关键逻辑
string leftString = serialize(root->left);
string rightString = serialize(root->right);
// 左 + 右 + 根 拼接字符串
// string nowString = leftString + rightString + to_string(root->val); // 过不了root = [10,2,22,1,12,1,1] 会输出[[1],[22,1,1]] 正确是:[[1]]
string nowString = leftString + ',' + rightString + ',' + to_string(root->val);
// 出现次数freq? 第一次出现就加入res
int freq = TreeMap[nowString];
if (freq == 1) {
res.push_back(root);
}
//
TreeMap[nowString]++;
return nowString;
}
};左 + 右 + 根 拼接字符串 拼接时候要注意的是 加逗号!!
否则有的会过不了!具体看注释!
110. 平衡二叉树
判断二叉树是否平衡,平衡的定义是:所有节点的左右子树高度差不超过1。
前面计算二叉树深度的题,拍脑袋的思路是遍历一遍二叉树,对每个节点计算左右子树的高度,然后高度+1,但是计算左右子树的高度这一步本身也是需要遍历左右子树所有节点的,所以这里存在大量重复计算;后来我们想到利用后序位置利用上子树算出来的高度,这样自底向上,成功优化!
这道题也是一样,其实本质还是计算深度,后序位置不断返回深度,并且判断当前左右子树平衡否即可;
cpp
class Solution {
public:
bool isBalanced(TreeNode* root) {
checkBalanced(root);
return balance;
}
private:
bool balance = true;
// 输入一个节点,计算当前节点的深度,后序位置可以计算左右子树的深度,并且判断是否平衡,
// 不平衡时立刻返回!结束递归
int checkBalanced(TreeNode* root) {
if (root == nullptr) return 0;
if (!balance) return 1010; // 随便返回一个数,不平衡时立即返回
int leftTreeMaxDepth = checkBalanced(root->left);
int rightTreeMaxDepth = checkBalanced(root->right);
if (abs(leftTreeMaxDepth - rightTreeMaxDepth)) balance = false;
return 1 + max(leftTreeMaxDepth, rightTreeMaxDepth);
}508. 出现次数最多的子树元素和
寻找重复的子树 中我们后序位置记录当前节点的序列化结果,用map记录每种子树出现次数,当某颗子树第二次出现时就记入答案,保证不重复记录!
这道题更简单些,后序位置记录当前节点为根的树的元素和,记录所有元素和出现的频次,最后返回出现次数最多的元素和对应的根节点,区别在于这次要的是所有出现次数最多的元素和!
cpp
class Solution {
// sum -> count
unordered_map<int, int> SumtoCount;
public:
vector<int> findFrequentTreeSum(TreeNode* root) {
sumTree(root);
}
private:
// 计算以当前节点为根的二叉树所有节点之和
int sumTree(TreeNode* root) {
if (root == nullptr) return 0;
// 要利用后序位置,先递归左右子树,
int leftSum = sumTree(root->left);
int rightSum = sumTree(root->right);
int res = root->val + leftSum + rightSum;
// 后序位置要记录
SumtoCount[res]++;
return res;
}
};二叉树 & 「层序遍历」思维
102. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
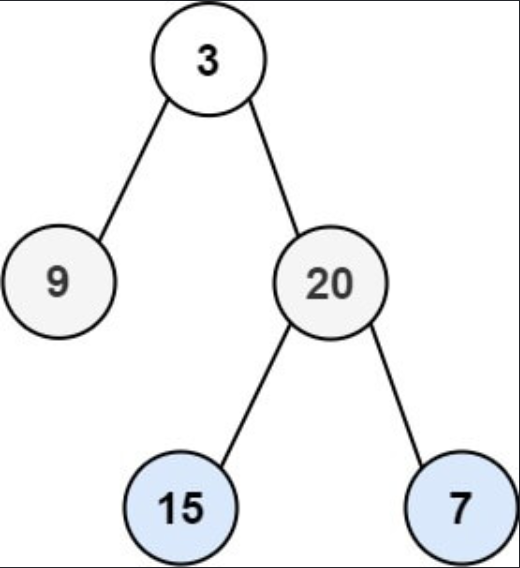
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> res;
if (root == nullptr) return res;
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
int thislevelNodeNum = q.size();
vector<int> thislevel;
for (int i = 0; i < thislevelNodeNum ;i++) {
TreeNode* curNode = q.front();
q.pop();
thislevel.push_back(curNode->val);
if (curNode->left != nullptr) q.push(curNode->left);
if (curNode->right != nullptr) q.push(curNode->right);
}
res.push_back(thislevel);
}
return res;
}
};107. 二叉树的层序遍历 II
这道题只需要改一行超简单。
如果是python,最后返回一个切片return result[::-1]不要太简单;
如果是cpp,要用迭代器插入到首部,像这样:
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> res;
if (root == nullptr) return res;
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
int thislevelNodeNum = q.size();
vector<int> thislevel;
for (int i = 0; i < thislevelNodeNum ;i++) {
TreeNode* curNode = q.front();
q.pop();
thislevel.push_back(curNode->val);
if (curNode->left != nullptr) q.push(curNode->left);
if (curNode->right != nullptr) q.push(curNode->right);
}
// res.push_back(thislevel);
// res.push_front(thislevel); 根本没有这东西呀!
res.insert(res.begin(), thislevel);
}
return res;
}
};另一种思路是DFS,这里简单写下:
python
from collections import deque
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:
# 特解:如果根节点为空 直接返回空列表
if not root:
return []
levels = []
def t(node, level):
if not node:
return
if len(levels) == level:
levels.append([])
levels[level].append(node.val)
t(node.left, level + 1)
t(node.right, level + 1)
t(root, 0)
return levels[::-1]103. 二叉树的锯齿形层序遍历
前两道题的杂交...无语的题,设置一个flag位控制当前层是从左往右还是从右往左即可。此外为了前后两种不同的添加方式,需要 用到队列,以及把队列添加到res时需要换成vector;
所以这道题既需要队列queue,也需要双端队列deque!
cpp
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> res;
if (root == nullptr) return res;
// 队列是一进一出,双端队列是两头都可以进出deque
queue<TreeNode*> q;
q.push(root);
bool flag = true;
while (!q.empty()) {
int level_size = q.size();
deque<int> level_dq;
for (int i = 0; i < level_size; i++) {
TreeNode* cur = q.front();
q.pop();
// 实现锯齿形 z形 遍历,dq中加入cur->val 并且 对应的左右子节点加入q
if (flag) { // 从左往右
level_dq.push_back(cur->val);
} else { // 从右往左
level_dq.push_front(cur->val);
}
// 将cur左右子节点加入队列q
if (cur->left != nullptr) q.push(cur->left);
if (cur->right != nullptr) q.push(cur->right);
}
// 这一层处理完,设置flag换方向
flag = !flag;
res.push_back(vector<int>(level_dq.begin(), level_dq.end()));
}
return res;
}
};