目录
一.基本思想
归并排序是采用分治法的一个非常典型的应用。它将已经有序的序列合并为完全有序的序列,即先使得每一个子序列有序,再让子序列之间有序。归并排序建立在归并操作上,以下动图能很好的演示归并排序中归并的过程:

但上图只展示了归并排序中归并的过程,没有对拆分过程的展示,接下来我将具体介绍归并排序的核心步骤。
已知对于两个已经有序的序列而言,使用p1和p2来比较,p1和p2中较小的一个一定就是当前最小的,放入临时数组tmp中,随后指向的p向后移动,再次进行比较,如此就能将两个有序的序列合并为一个有序序列,这就做到了排序。

然而,如何得到两个已经有序的序列呢?这是类似问题,与排序整个序列的主问题是类似的,很明显,已经可以猜到要使用递归来实现了,那么只需要将两个无序序列进行再次拆分,直到序列中仅剩一个数据,那么此时就可以看作是有序的了,这就是拆分过程。
拆分结束后,就进行归并,每两个已有序的序列合并到一起,再和其他已合并的序列进行合并,最终合并为一个序列,这就是排序后得到的最终结果,下图展示了整个过程:

具体应该如何拆分?拆分也是有讲究的,不注意会产生问题。一般都会想到取中分割,取序列左端为begin,右端为end,mid自然等于(begin+end)/2,那么就可以围绕mid拆分为左右两个序列,其中mid应该包含在左端,否则会造成死循环,也就是应该分为[begin,mid]和[mid+1,end],证明如下:

二.递归版本
cpp
//归并排序-主体
void _Merge(int* a, int* tmp, int begin, int end)
{
//结束条件
if (begin >= end)
return;
//拆分
int mid = (begin + end) / 2;
_Merge(a, tmp, begin, mid);
_Merge(a, tmp, mid + 1, end);
//归并
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
//归并排序
void Merge(int* a, int n)
{
//创建临时数组
int* tmp = (int*)malloc(sizeof(int) * n);
_Merge(a, tmp, 0, n - 1);
free(tmp);
tmp = NULL;
}三.非递归版本
对于非递归版本,就不用考虑拆分的过程了,直接将一个数组看作单个有序的状态开始归并。使用gap来模拟归并的过程,如下所示:

根据上述过程可以得到以下代码,但这样的写法却存在一些问题 ,不妨打印出来看看
cpp
//归并排序-主体-(非递归)
void Merge_NonR(int* a, int n)
{
//创建临时数组
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
//gap控制每组归并的数据个数
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + gap * 2 - 1;
printf("[%d %d],[%d,%d]", begin1, end1, begin2, end2);
int j = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
}
gap *= 2;
printf("\n");
}
}
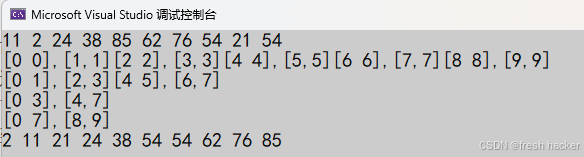
可以很明显的看到,在只有10个数据的时候(有效下标为0到9),发生了数组越界的问题 ,那么这就还需要在程序中加入对应的解决方法,从上图可以发现,只要是begin2(上图的10和12)出现了越界(大于等于n)那么后一个序列就是非法的,也就不用归并了,此时可以直接跳出循环直接到下一个gap,那么到最后一轮,end2是越界的(如上图15)此时8到9是有序的,只需要调整end2为9(即n-1)即可。完整实现的代码如下:
cpp
//归并排序-主体-(非递归)
void Merge_NonR(int* a, int n)
{
//创建临时数组
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
//gap控制每组归并的数据个数
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + gap * 2 - 1;
if (begin2 >= n)
break;
if (end2 >= n)
end2 = n - 1;
printf("[%d %d],[%d,%d]", begin1, end1, begin2, end2);
int j = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
}
gap *= 2;
printf("\n");
}
}四.特性总结
1.时间复杂度:O(N*logN)
依据二分往下递归,类似于二叉树,总共有LogN层,每层总的归并合计起来可以看作O(N),因此总的时间复杂度可以看作是:O(N*logN)
2.空间复杂度:O(N)
由于开辟了一个大小为N的额外数组,因此归并排序的空间复杂度为O(N)