前面分享了带置信区间的折线图和带置信区间的折线散点图的绘图教程:
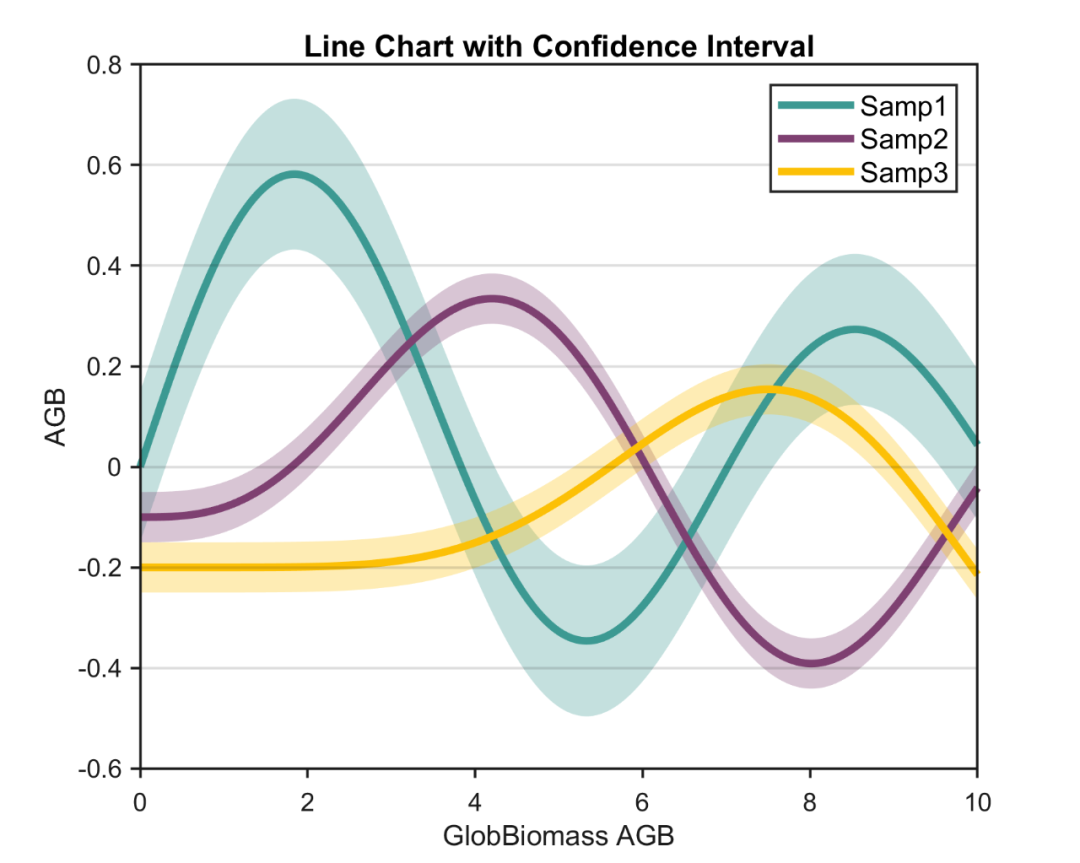
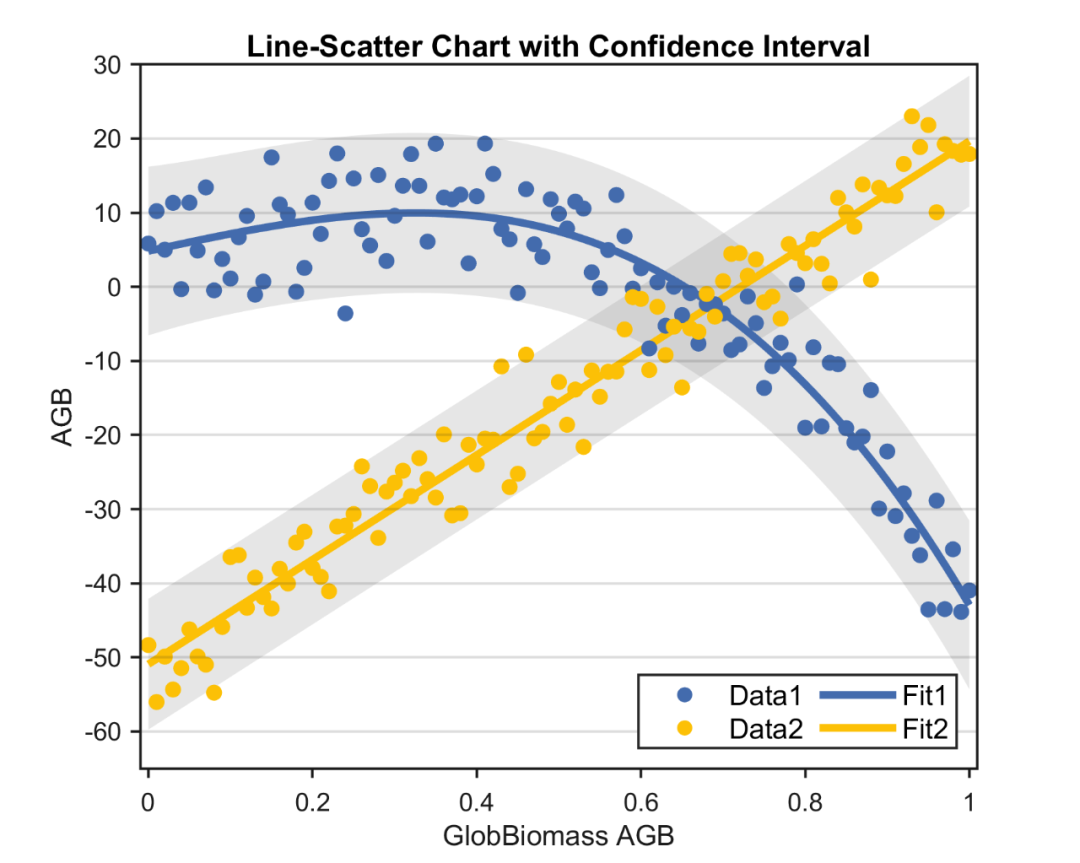
很多人表示,昆哥,图是很好看啦,但咱不会求置信区间啊,咋办嘞?
说实话,这种事情属于数据处理,一般都是在画图前解决的,所以我在教程中是不会体现的。
另一方面,数据处理工作涉及面太广,很多我自己用不到,也就不会深入研究,更谈不上出干货教程(但不影响画图)。
不过,最近这不学会ChatGPT了嘛,搞不定找他呗。
Matlab&ChatGPT计算置信区间
首先,为了防止他随便编个代码骗我,我从《Nature》论文中找到一幅带置信区间的折线散点图:
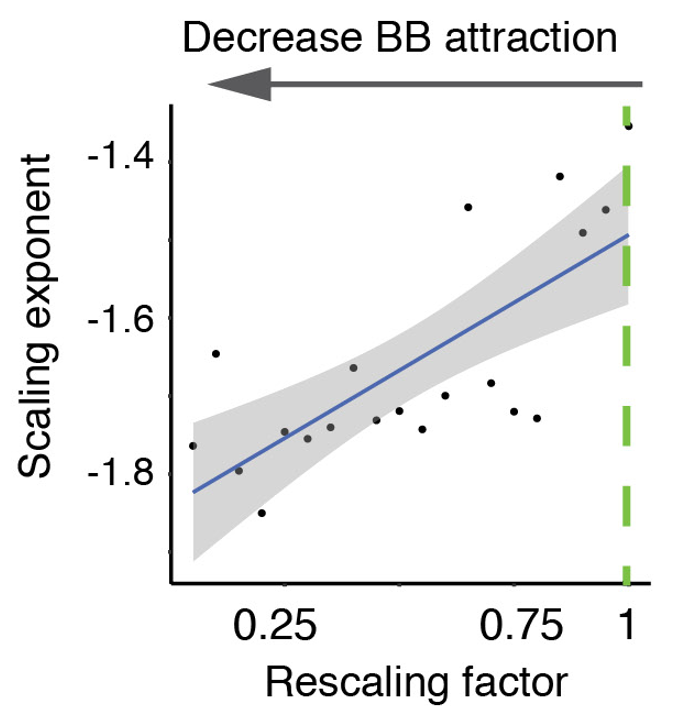
利用之前分享的图片数据提取工具,提取其中的离散点,作为原始数据,而图片本身作为验证信息,检验ChatGPT给出的结果是否正确。
然后,向ChatGPT中提问:

这是他给出的代码:
% 数据准备data = [0.046053 0.096491 0.14912 0.19518 0.24342 0.30044 0.3443 0.39474 0.44737 0.5 0.54825 0.59649 0.70175 0.74781 0.80044 0.64912 0.85088 1.0044 0.95175 0.90132; -1.7629 -1.6466 -1.7949 -1.8486 -1.7438 -1.754 -1.7412 -1.662 -1.731 -1.7195 -1.7412 -1.699 -1.6837 -1.7195 -1.7272 -1.4575 -1.4166 -1.3553 -1.4639 -1.4895];x = data(1, :);y = data(2, :);% 线性拟合[p, S] = polyfit(x, y, 1);% 计算拟合直线的y值y_fit = polyval(p, x);% 计算标准误差n = length(y); % 样本数量y_residual = y - y_fit; % 残差SSE = sum(y_residual.^2); % 残差平方和sy = sqrt(SSE / (n - 2)); % 残差标准差% 计算置信区间alpha = 0.05; % 置信水平 95%t_value = tinv(1 - alpha/2, n - 2); % 学生 t 分布临界值x_mean = mean(x); % x 的均值Sxx = sum((x - x_mean).^2); % x 的方差和delta = t_value * sy * sqrt(1/n + (x - x_mean).^2 / Sxx); % 置信区间% 可视化figure;plot(x, y, 'bo'); % 原始数据点hold on;plot(x, y_fit, 'r-', 'LineWidth', 2); % 拟合直线plot(x, y_fit + delta, 'r--', 'LineWidth', 1.5); % 上置信区间plot(x, y_fit - delta, 'r--', 'LineWidth', 1.5); % 下置信区间legend('原始数据', '拟合直线', '置信区间', 'Location', 'Best');xlabel('x');ylabel('y');title('带噪声离散点的线性拟合及其置信区间');hold off;将代码复制粘贴到Matlab,得到结果:
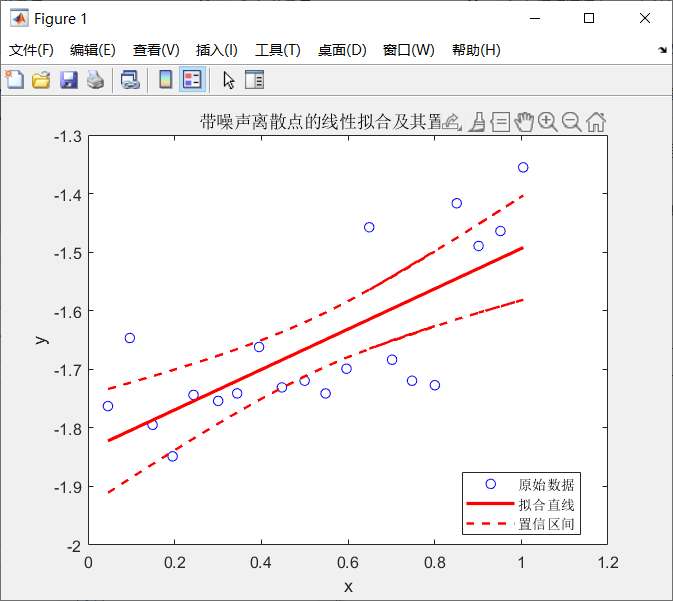
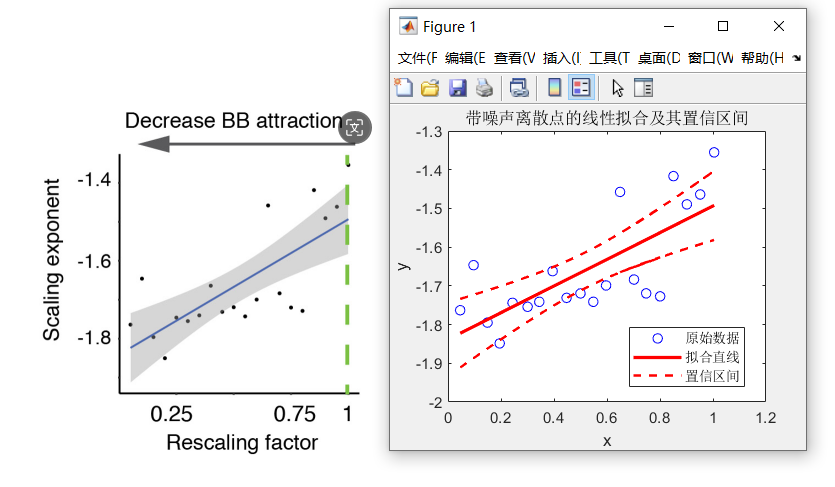
可以看到,除了图片比例之类的细节问题,结果图的整体趋势同验证图没啥区别,说明ChatGPT给的代码没问题。
简单调一下绘图细节:
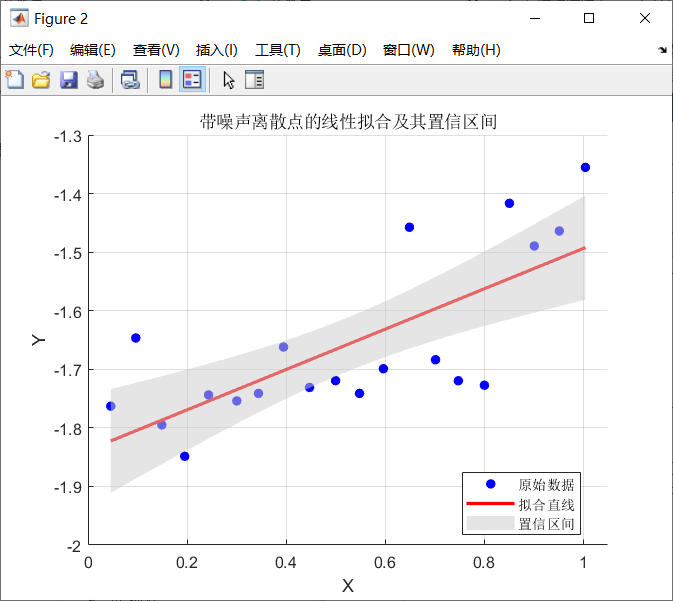
保险起见,我又问了一下置信区间的计算原理,这是他给出的答案:



找了一下网上相关内容,基本也是大差不差,说明他还是很靠谱的。
以上。