摘要:
1,Bellman-Ford 算法的介绍
2,Bellman-Ford 算法为什么可以解决有负权边的图
3,Bellman-Ford 算法为什么不能解决有负权回路的图
4,Bellman-Ford 算法的代码实现和负权回路的判断
5,Bellman-Ford 算法的代码优化
1,Bellman-Ford算法的介绍
贝尔曼-福特算法(Bellman-Ford algorithm)和迪杰斯特拉算法(Dijkstra)一样也是求单源点最短路径的,但Dijkstra算法不能解决有负权边的图,如果想要解决有负权边的图可以使用 Bellman-Ford 算法。
解题思路就是假设有一条边 [begin,end,value] ,如果 dis[begin] + value < dis[end] ,我们可以更新 dis[end] 的值为 dis[begin] + value ,如下图所示,0 到 2 的距离如果经过顶点 1 会更小。
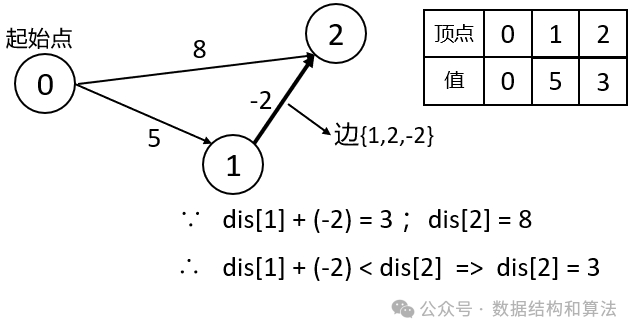
所以我们只需要枚举所有的边即可,代码如下:
go
for (int[] edge : edges) {// 遍历边。
int begin = edge[0];// 边的起点。
int end = edge[1];// 边的终点。
int value = edge[2];// 边的权值。
if (dis[begin] + value < dis[end])// 松弛。
dis[end] = dis[begin] + value;
}如果只枚举一遍的话,有可能只会更新和起始点邻接的点(也就是起始点直接指向的点),与起始点没有邻接的点可能没更新,也可能更新了,这个和边的更新顺序有关,如下图所示。
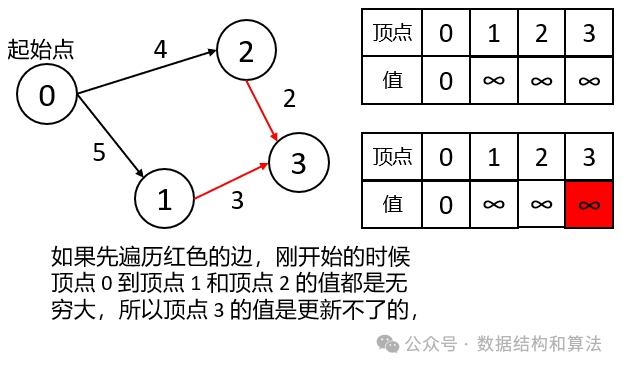
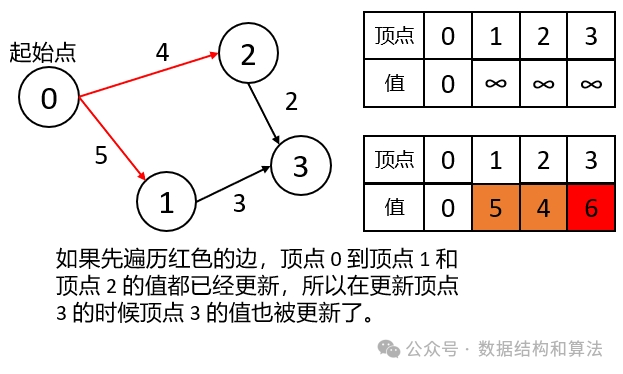
也就是说如果枚举一遍,至少可以更新从起始点通过一条边到达的点,枚举两遍至少可以更新从起始点通过两条边到达的点 ...... 。在一个含有 n 个顶点的图中,一个点最多只能有 n-1 条边和起始点相连。所以我们最多只需要枚举 n-1 次即可计算从起始点到其他所有点的距离。