文章目录
1.01方程组的几何解释
对于二元方程组:row picture
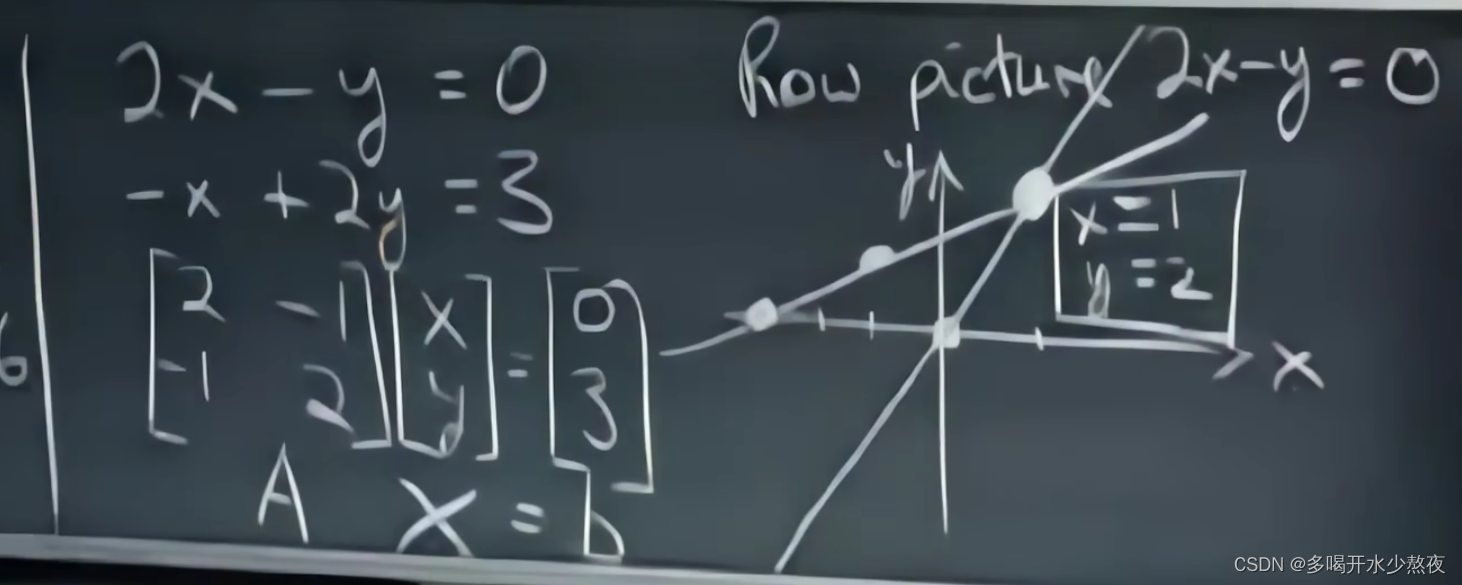
方程转化为矩阵 * 向量 = 向量的形式,并且二维三维可以用图像几何表示出来(解析几何)
用column picture进行表示(线性组合):
x [ 2 − 1 ] + y [ − 1 2 ] = [ 0 3 ] x\begin{bmatrix}2 \\ -1 \\ \end{bmatrix}+y\begin{bmatrix}-1 \\ 2 \\ \end{bmatrix}= \begin{bmatrix}0 \\ 3 \\ \end{bmatrix} \\ x[2−1]+y[−12]=[03]
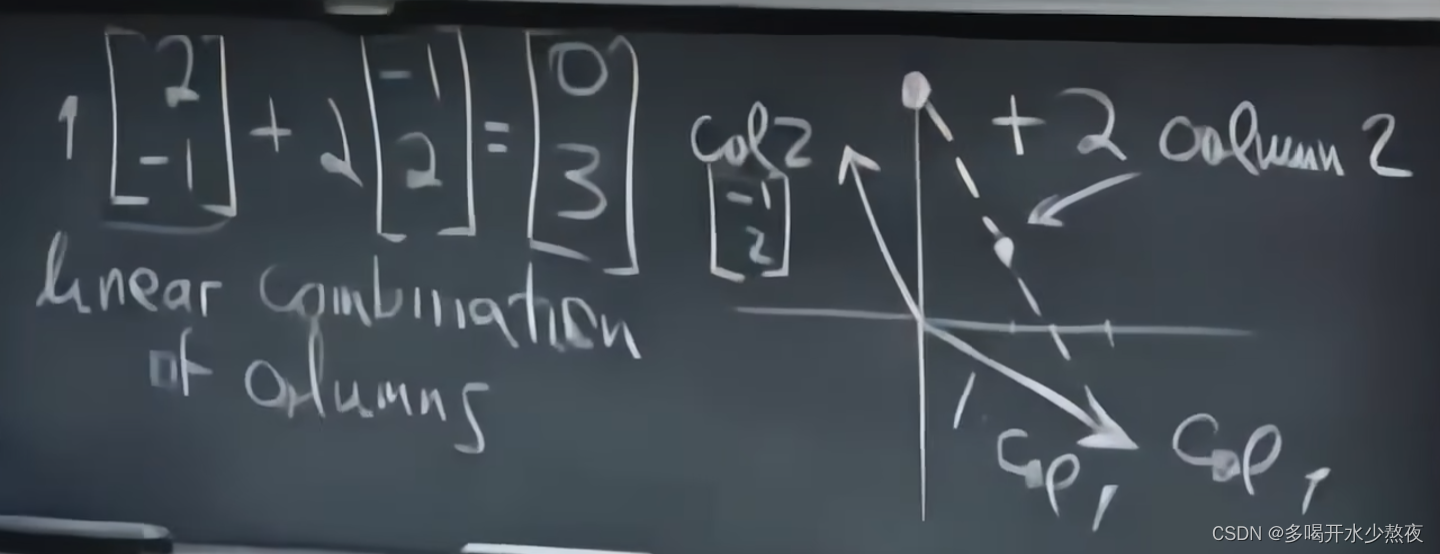
x=1,y=2,上述是用向量的角度进行求解。
任意两个不共线的非零向量能够表示平面中的任意向量
对于三元方程组:row picture
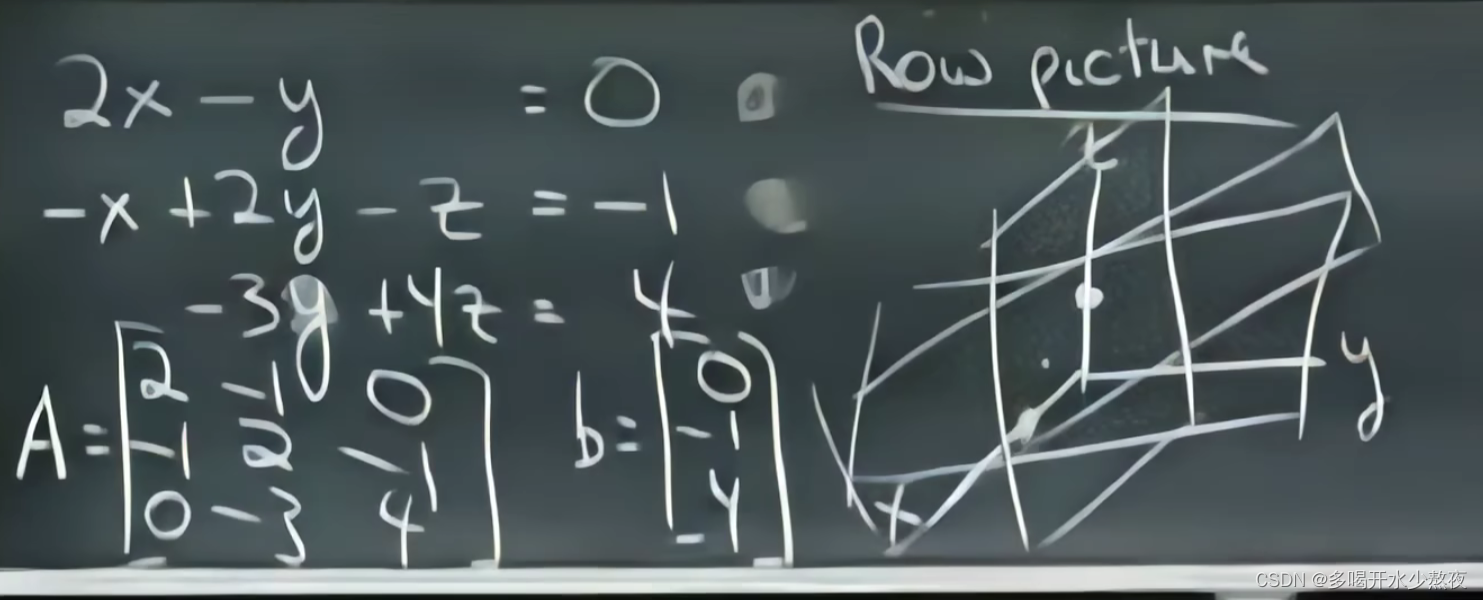
column picture(向量表示):
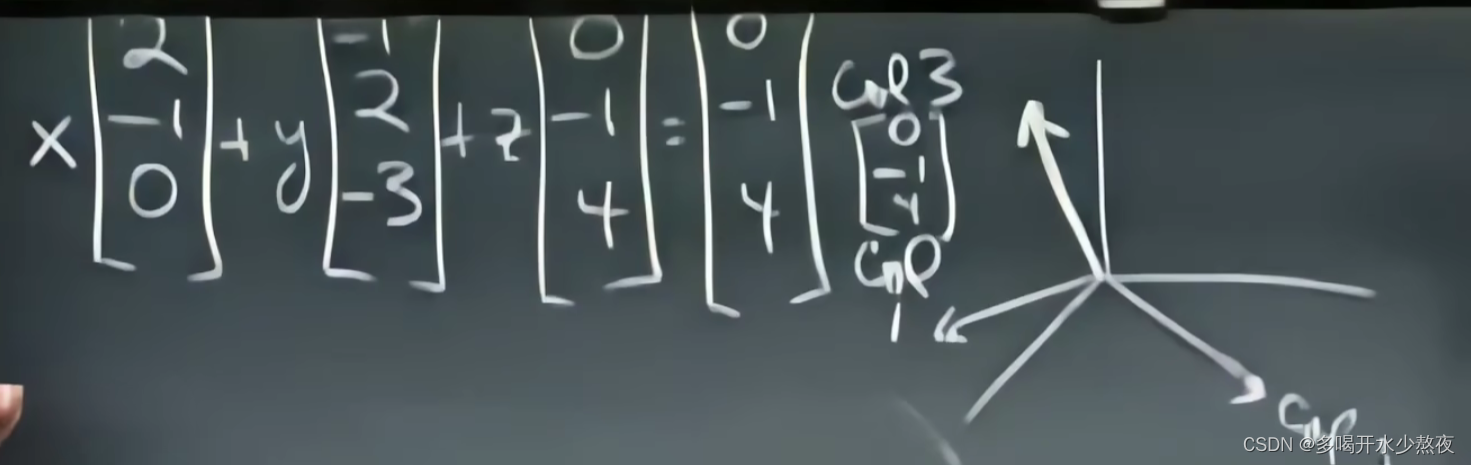
x=0,y=0,z=1
A x = b Ax=b Ax=b
是否对于任意b都有上式可解 = 列的线性组合是否能覆盖整个三维(n维)空间
非奇异矩阵/可逆矩阵可达到上面的要求(可逆矩阵被称为非奇异矩阵,因为可逆矩阵的行列式不为0,在数学中如果一个矩阵的行列式为0,则称这个矩阵为奇异矩阵。)
是3个向量都处于同一平面,即维度减一,所以涉及第三维度的向量b无法构造。
对于n个向量也是如果最后消解只有n-1维那也无解(一种平面只能覆盖n维空间的某n-1维平面,最后的求解也只能在这n-1维平面展开)。
方程组的矩阵形式:
A x = b ( A x 看做 A 各列的线性组合 ) Ax=b(Ax看做A各列的线性组合) Ax=b(Ax看做A各列的线性组合)
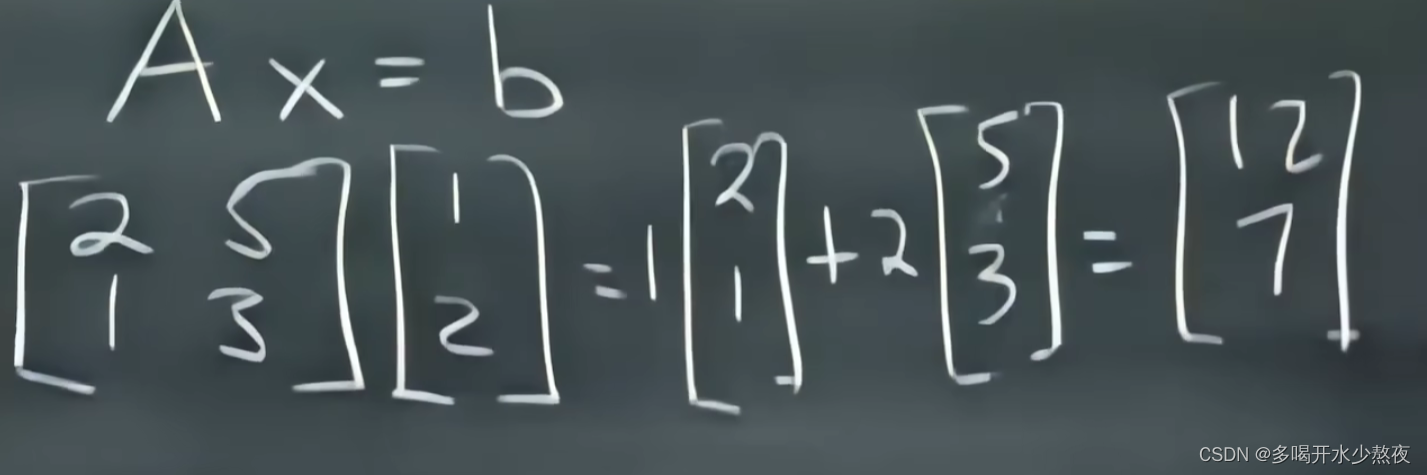
2.02矩阵消元
x + 2 y + z = 2 3 x + 8 y + z = 12 4 y + z = 2 A = [ 1 2 1 3 8 1 0 4 1 ] x+2y+z=2\\ 3x+8y+z=12\\ 4y+z=2\\ A=\begin{bmatrix}1 & 2 & 1 \\3 & 8 & 1 \\0 & 4 &1 \end{bmatrix} x+2y+z=23x+8y+z=124y+z=2A= 130284111
消元
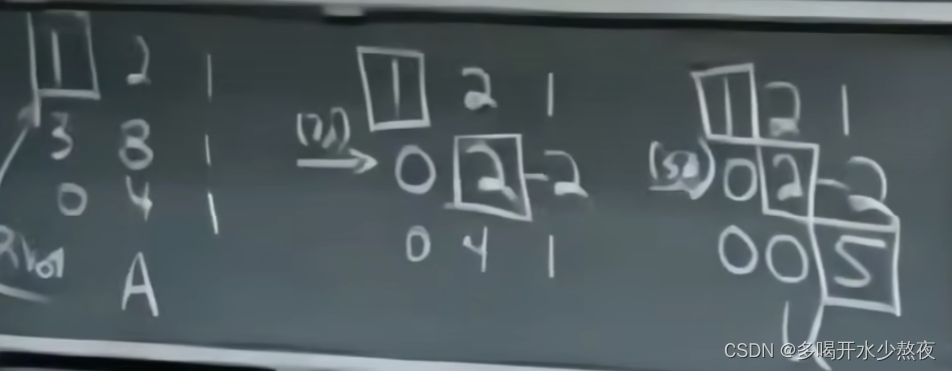
增广矩阵:Ab
回代(也就是加入b进行求解)

方程从上往下消元,从下往上回代求解
消元矩阵:
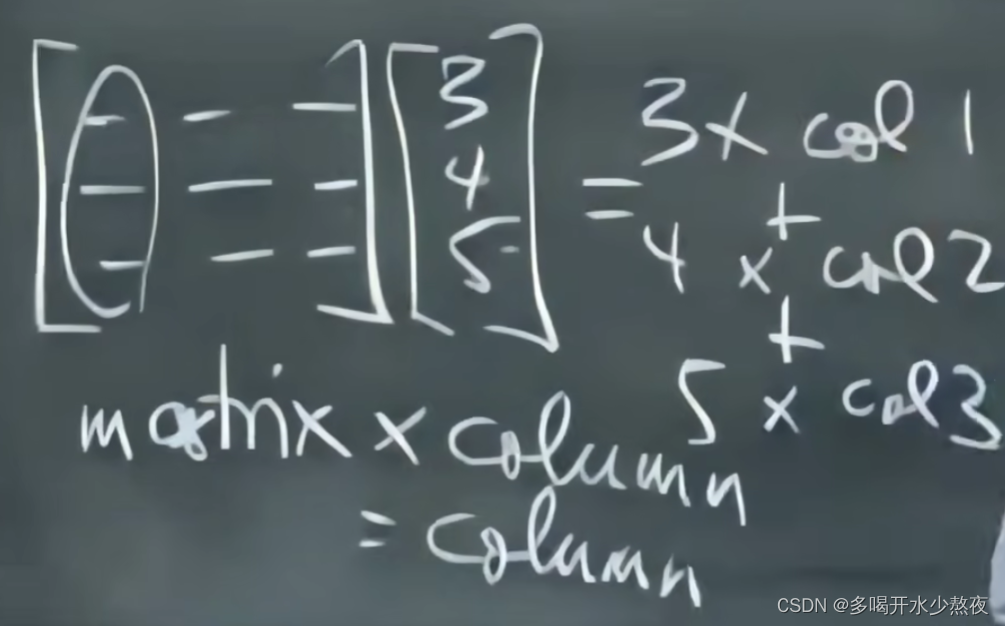
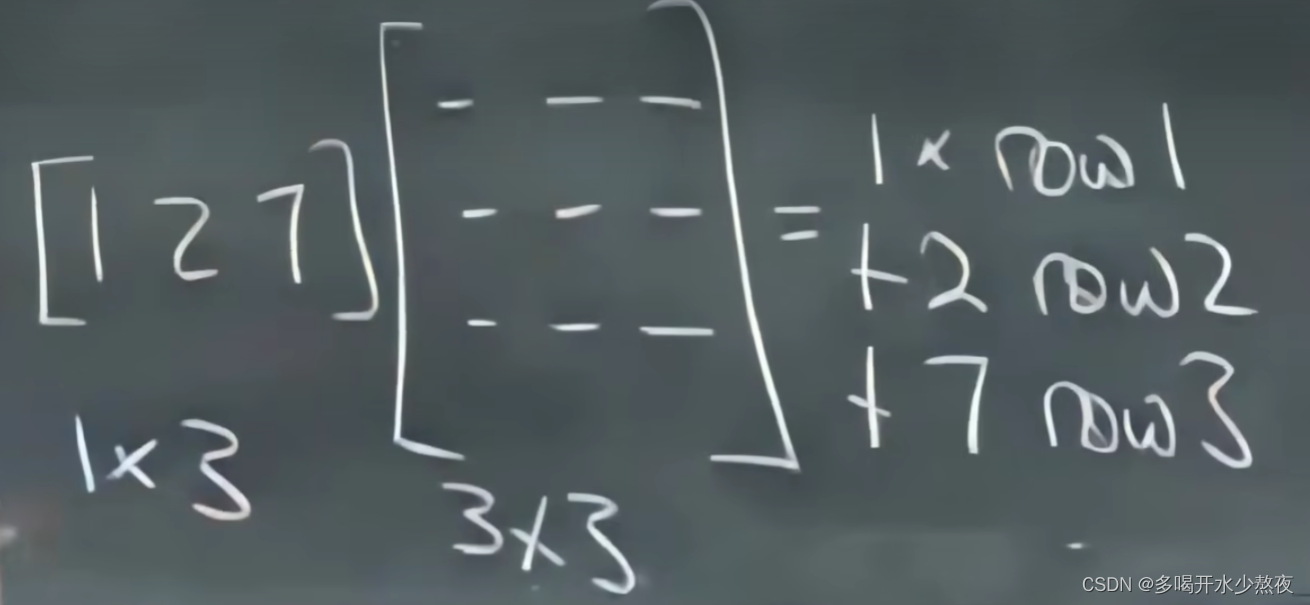
由上式可知,我们把左边的矩阵(初等矩阵)当成3个1*3的行向量,右边的结果的第一行=左边第一行的第一个数 * 中间第一行 + 左边第一行的第二个数 * 中间第二行 + 左边第一行的第三个数 *中间第三行,所以结果为:1,0,0,以此类推第二行为-3,1,0(-3 * 中间第一行+1 * 中间第二行),第三行为0,0,1

E 21 表示初等矩阵第二行第一个位置发生了变换:变为 0 E_{21}表示初等矩阵第二行第一个位置发生了变换:变为0 E21表示初等矩阵第二行第一个位置发生了变换:变为0
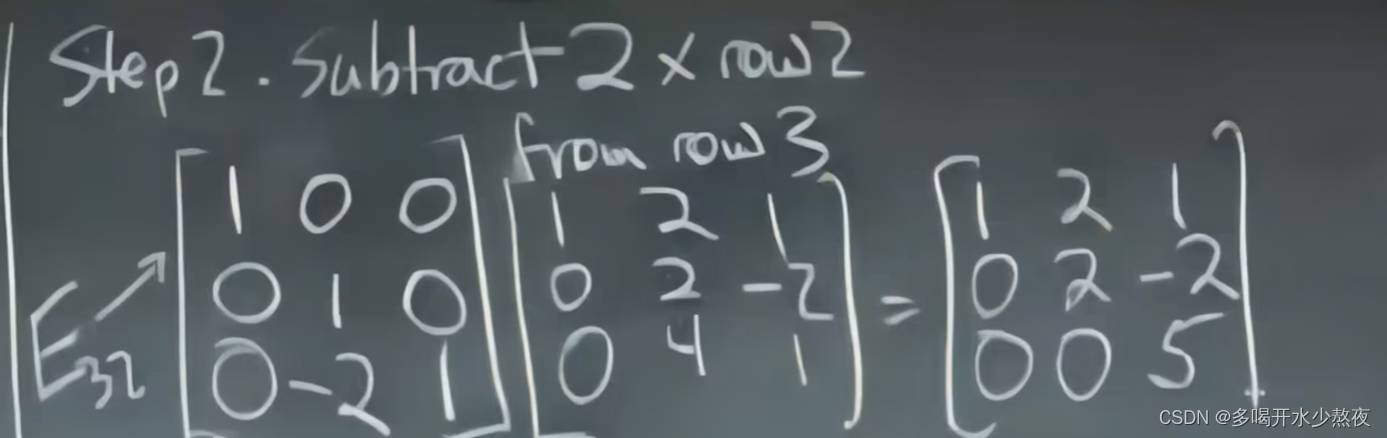
E 32 ( E 21 A ) = U 相当于 ( E 32 E 21 ) A = U 结合律 E_{32}(E_{21}A)=U \\ 相当于(E_{32}E_{21})A=U\\结合律 E32(E21A)=U相当于(E32E21)A=U结合律
置换矩阵P

行变换左乘,列变换右乘
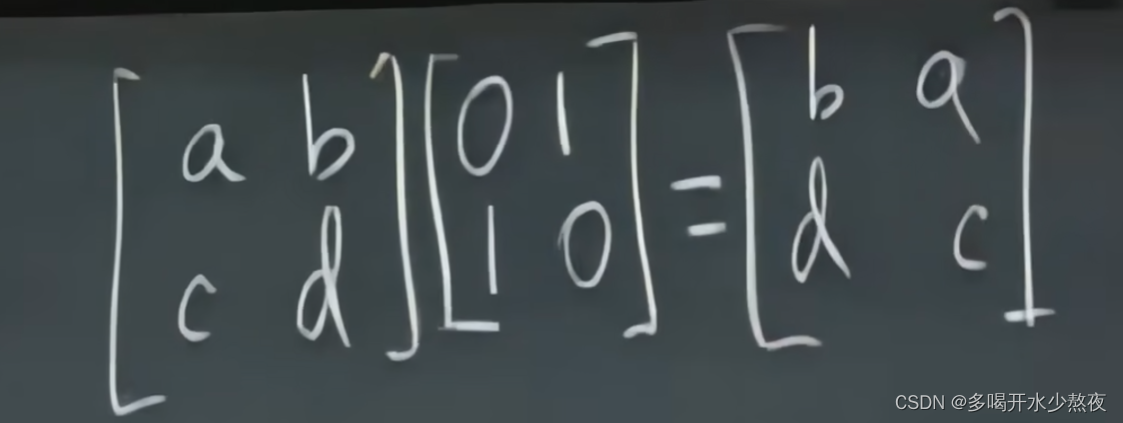
矩阵中基本没有交换律
逆矩阵:从U变回A
我们要取消这次消元,我们就希望E'EA=A,所以让E'E等于单位矩阵即可,E'是逆矩阵
变换后的矩阵EA,如何变回A?以行变换为例(左侧乘),就是找一个矩阵X使得XEA为A,此时若XE为单位阵,则XEA为A

E − 1 E = I E^{-1}E=I E−1E=I
3.03乘法和逆矩阵
乘法
方法一:行与列之间的点积
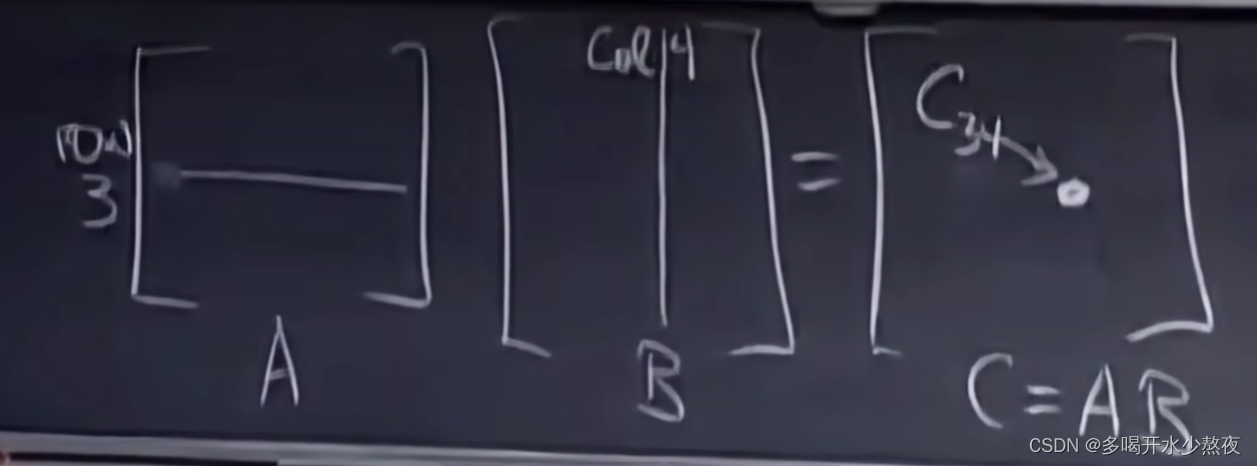
C 34 = ( r o w 3 o f A ) ⋅ ( c o l u m n 4 o f B ) C_{34}=(row3ofA) ·(column4ofB) C34=(row3ofA)⋅(column4ofB)
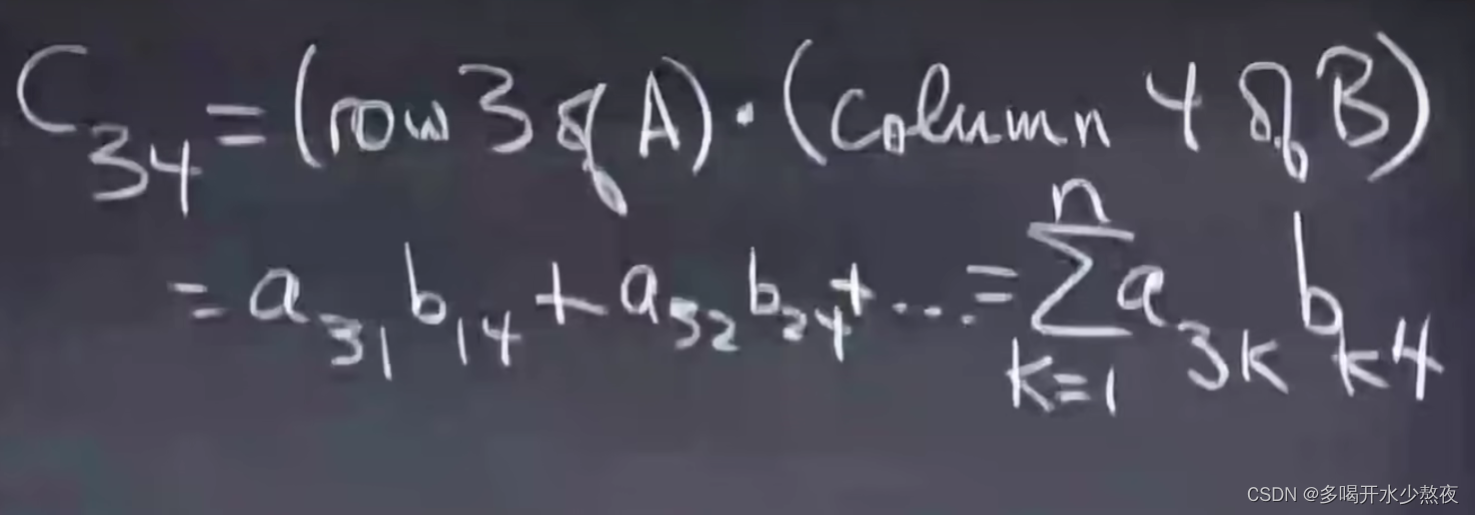
A是m * n,B是n * P,C=AB大小为m * P
方法二:把B看做是P个单独的列向量,像上一节课一样对每个列向量单独乘积最后再合并:
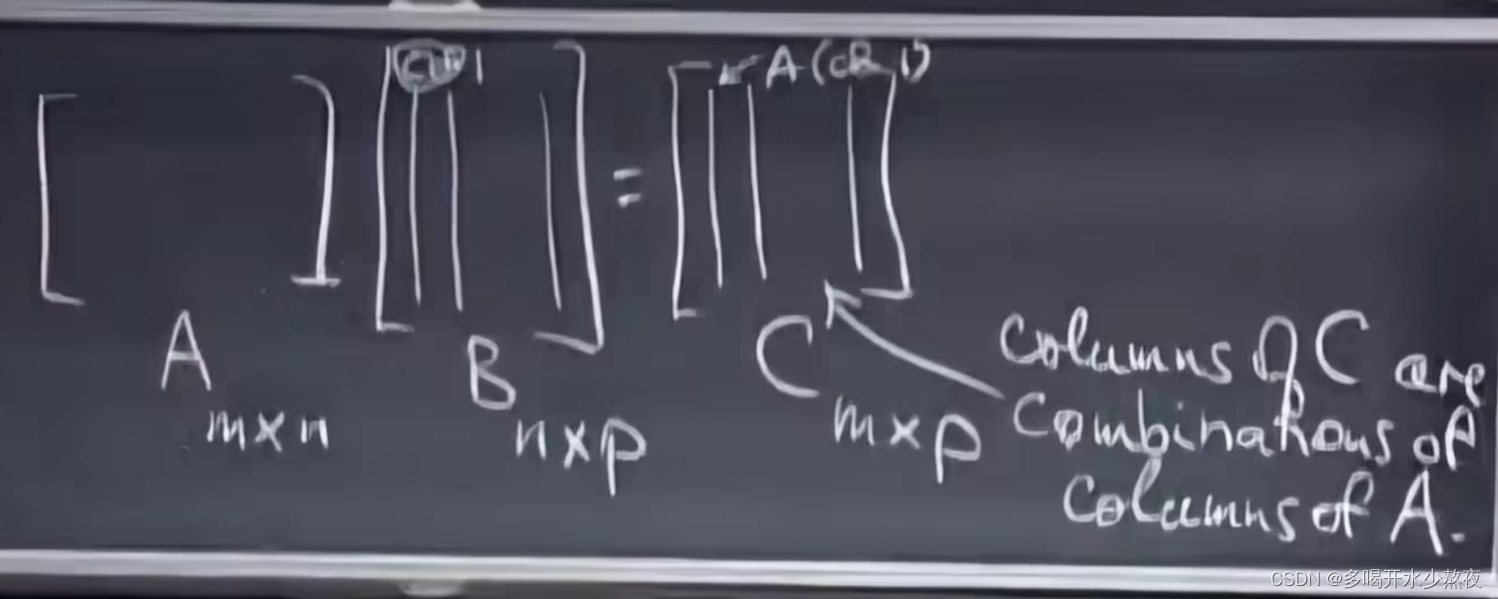
方法三:把A看做m个单独的行向量,向上节课一样对每个行向量单独乘积最后再合并:
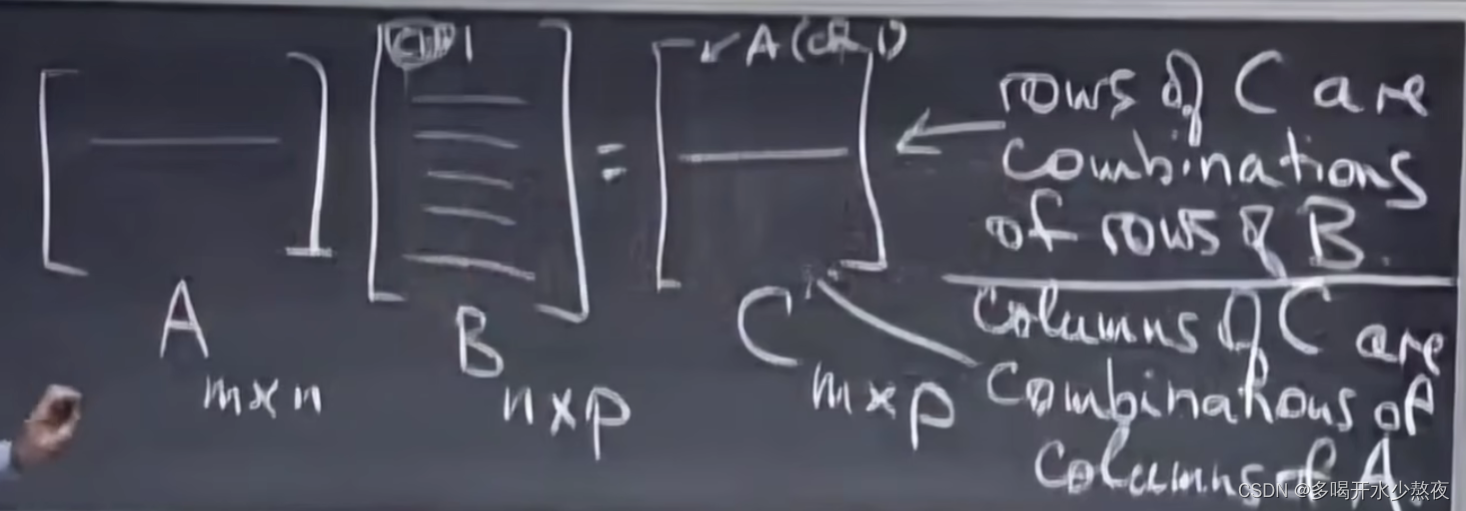
方法四:A中的列 * B中的行

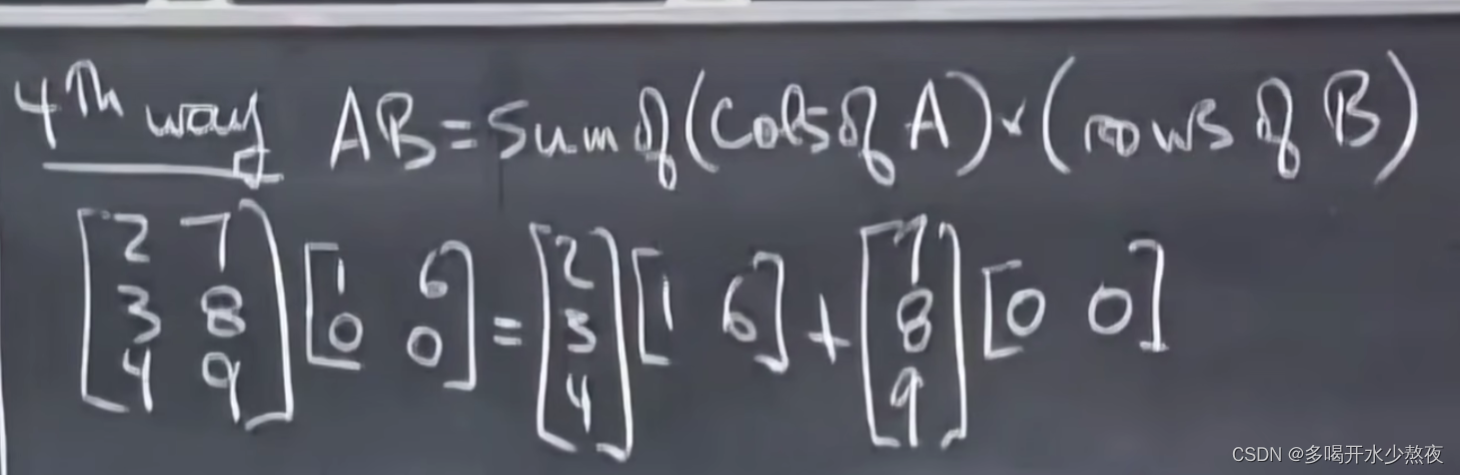
矩阵分块:把每个块都看成单独的元素运用方法一就得到下图
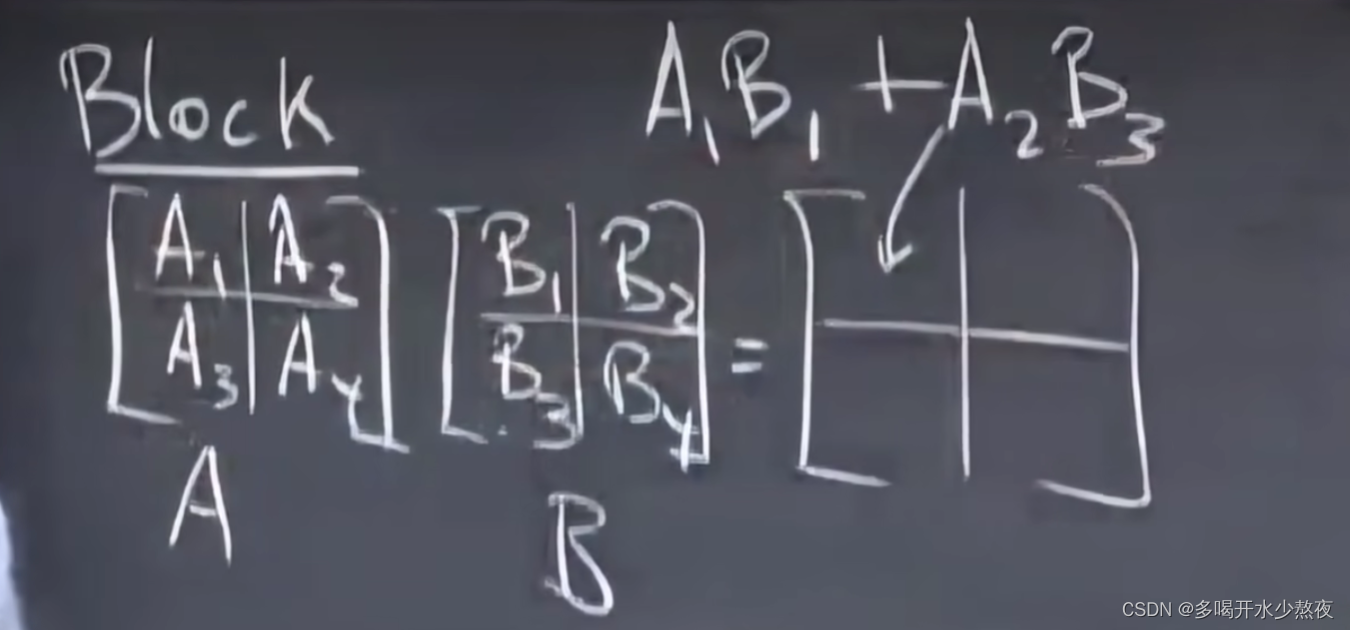
逆
逆矩阵(非奇异矩阵) * 原矩阵 = I(单位矩阵)
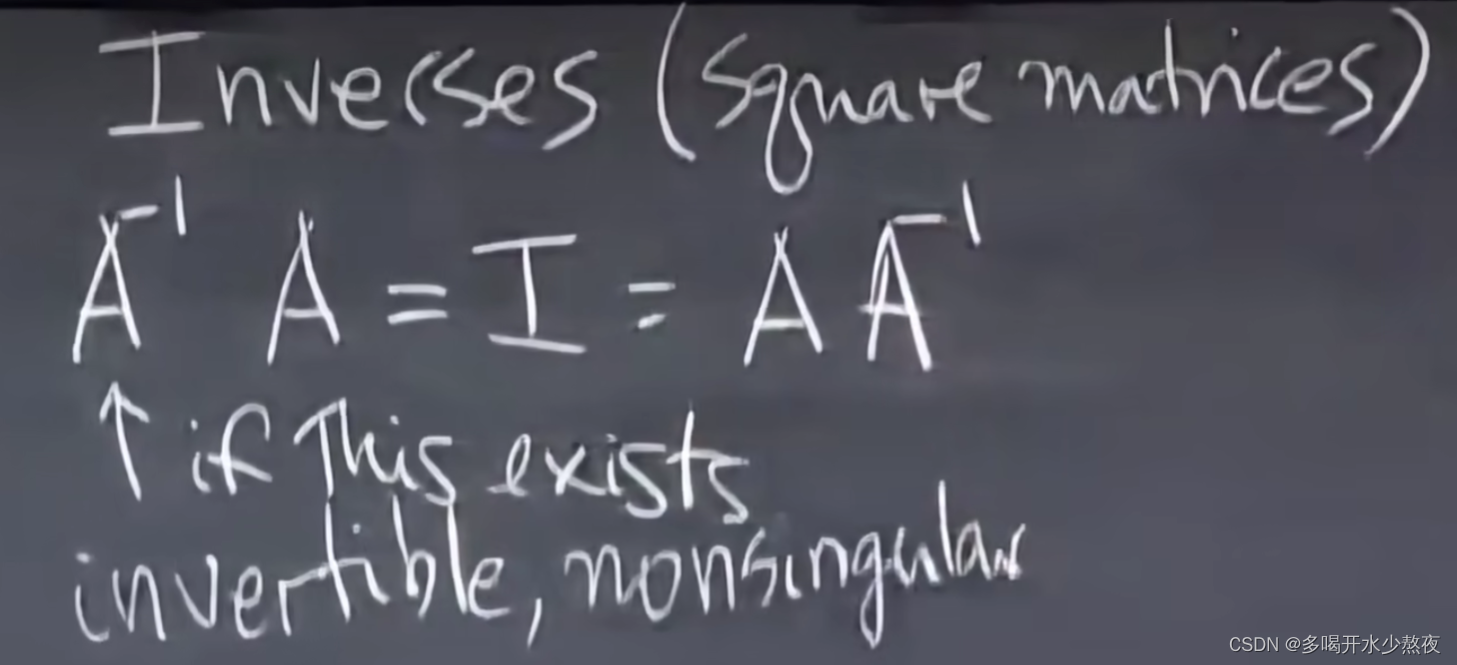
奇异矩阵(非逆)可以找到一个向量x 使得Ax=0,也就是A中的向量组共面
Ax=0 有非零解,说明A中有的列没有贡献,所以不可逆
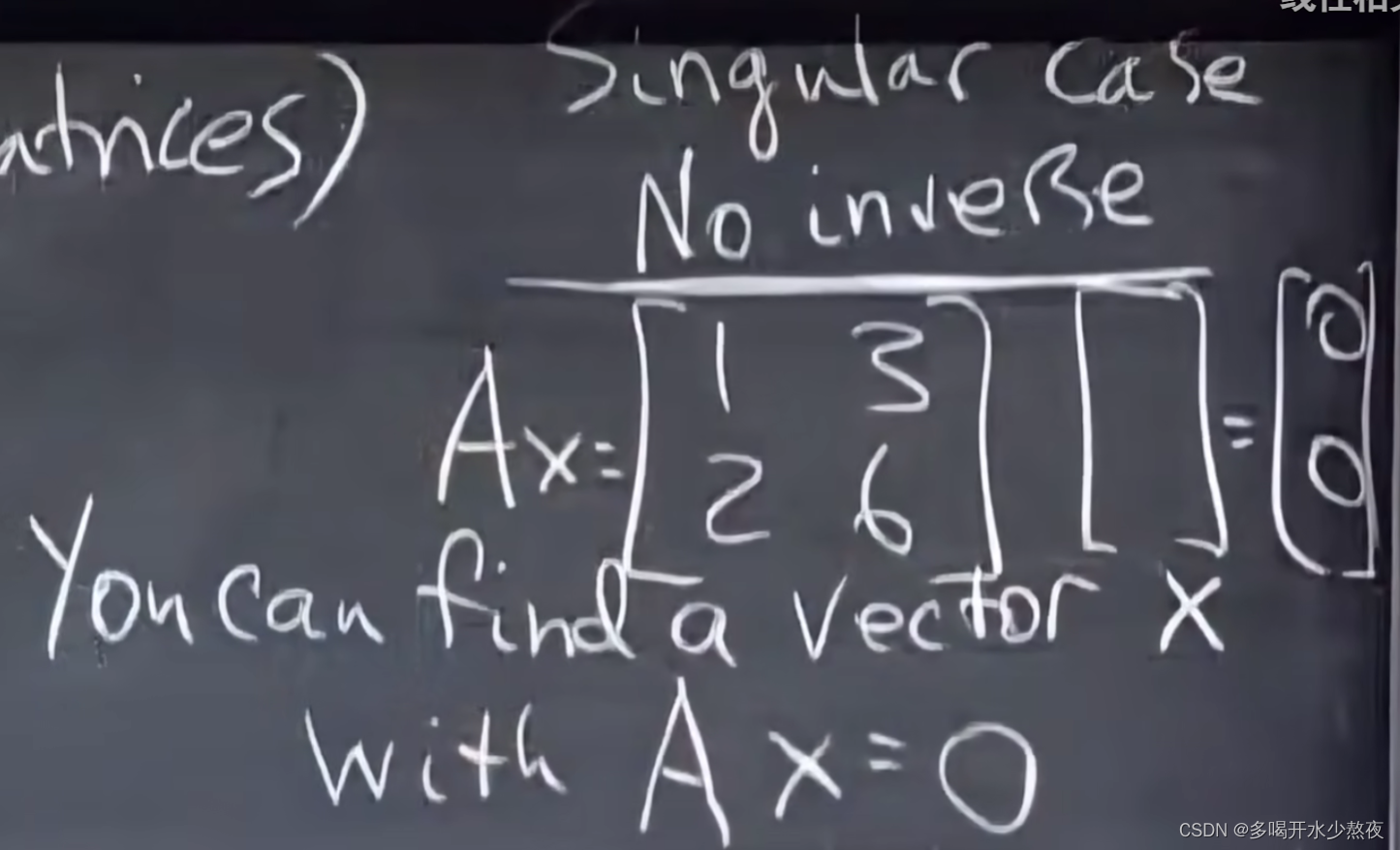
反证法:逆乘原得到单位矩阵,单位矩阵乘任一矩阵得原矩阵,所以得到X=0,但是X≠0,所以不成立
如何求逆矩阵:对于下列矩阵本质上就求两个二元一次方程组
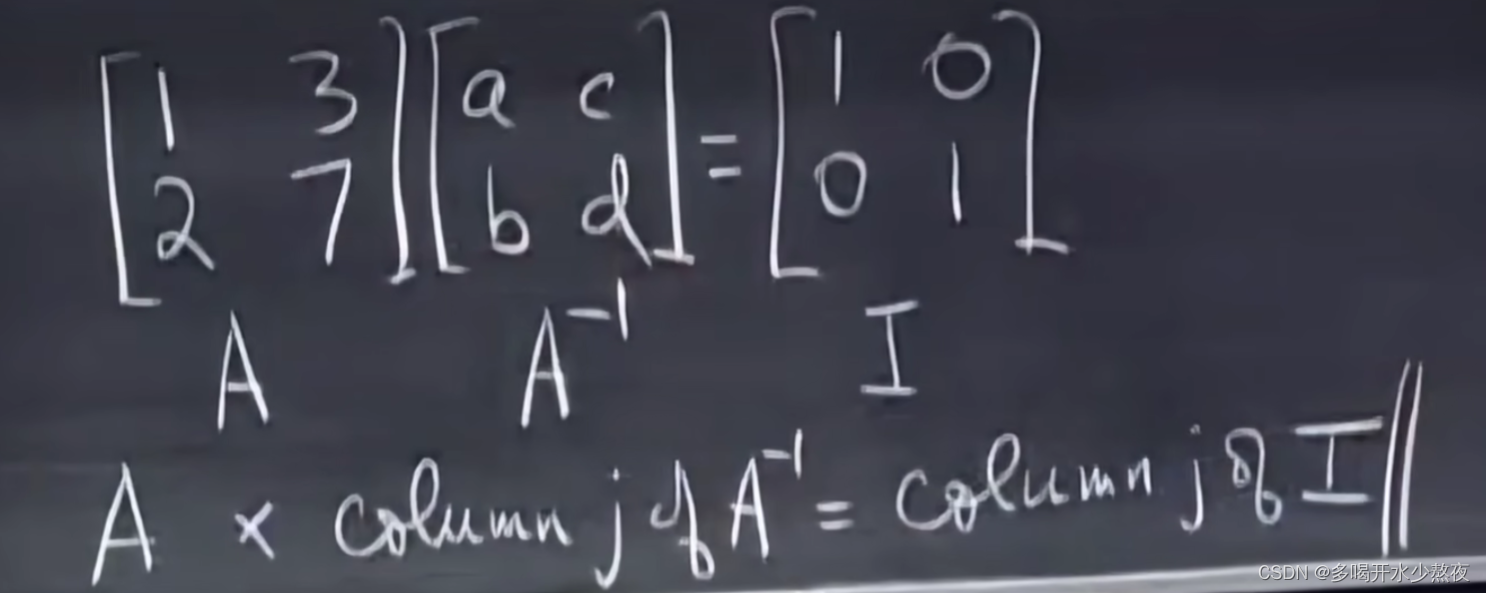
同时求解两个方程:增广矩阵形式
高斯-若尔当消元法:

原理可理解为,假定有B矩阵,BA=I,那么右乘A逆得BI=A逆,如此可以得到逆矩阵
相当于对AI同时乘以A逆,得到I和A逆
A I = = > A ∗ A ′ I A ′ = = > I A ′ AI==>A*A^{\prime}I{\,}A^{\prime}==>IA^{\prime} AI==>A∗A′IA′==>IA′
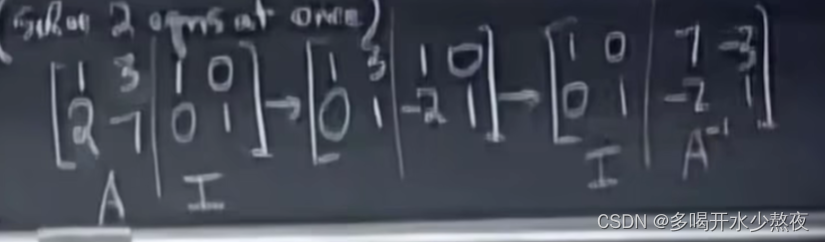
4.04矩阵A的LU分解
两矩阵相乘,且它们的逆均已知,那么AB的逆是什么 B − 1 A − 1 B^{-1} A^{-1} B−1A−1
A转置乘以A逆的转置等于单位E,定理A转置乘以A转置的逆等于单位E,所以A逆转置等于A转置的逆
如果还是不明白,因为我们已经知道A * A逆=A逆 * A=E,所以下面那个式子还可以写成,A转置的逆*A的转置=E,逆矩阵又是唯一的,所以A逆的转置=A转置的逆
这个由"行"组成的系数矩阵的每一行应该和之前A-1代表的系数矩阵的"列"相对应,因此就是(A-1)T*AT
将原本的A*A-1=I中左侧的A中的所有列看作用于线性组合的列向量,A-1中的每一列代表每次线性组合的系数组成
A A − 1 = I ( A − 1 ) T A T = I ( A − 1 ) T = ( A T ) − 1 AA^{-1}=I\\ (A^{-1})^TA^T=I\\ (A^{-1})^T=(A^{T})^{-1} AA−1=I(A−1)TAT=I(A−1)T=(AT)−1
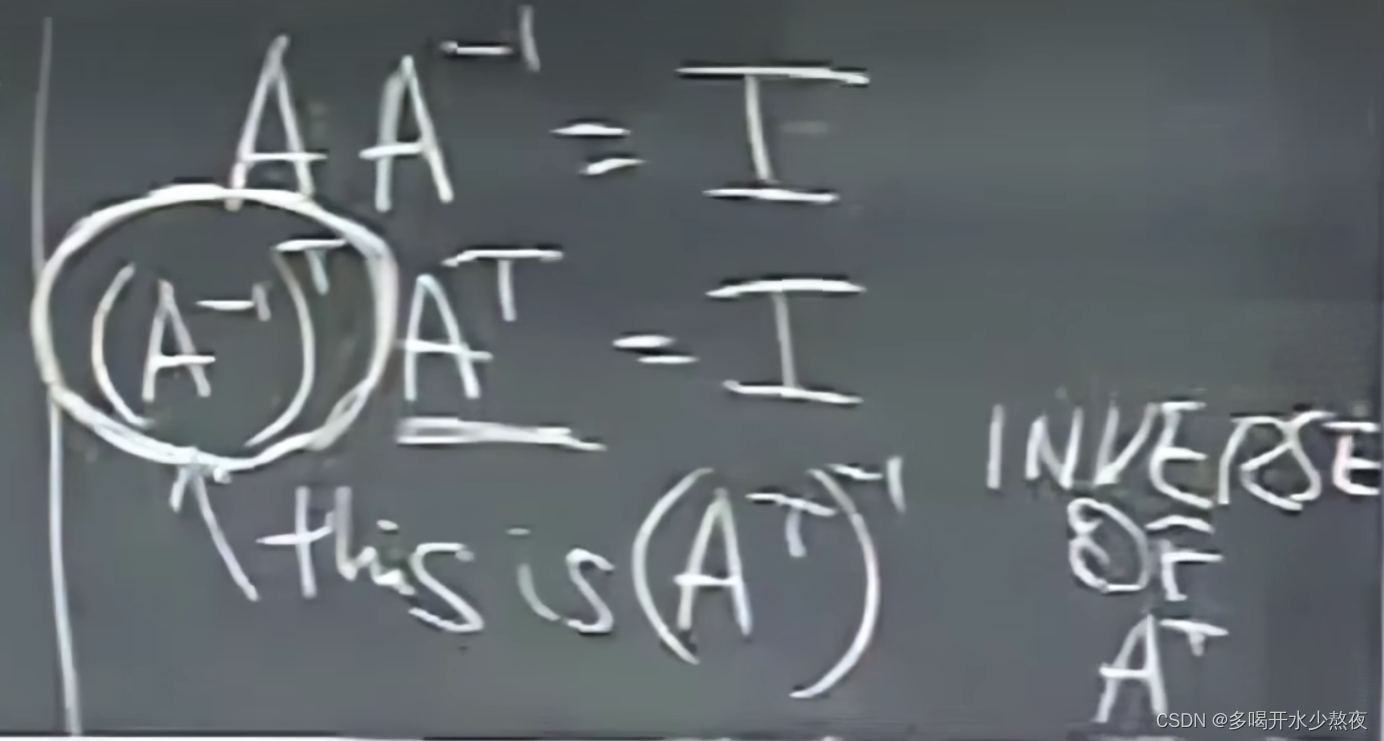
把-4倍的第一行和1倍的第二行相加,放到第二行
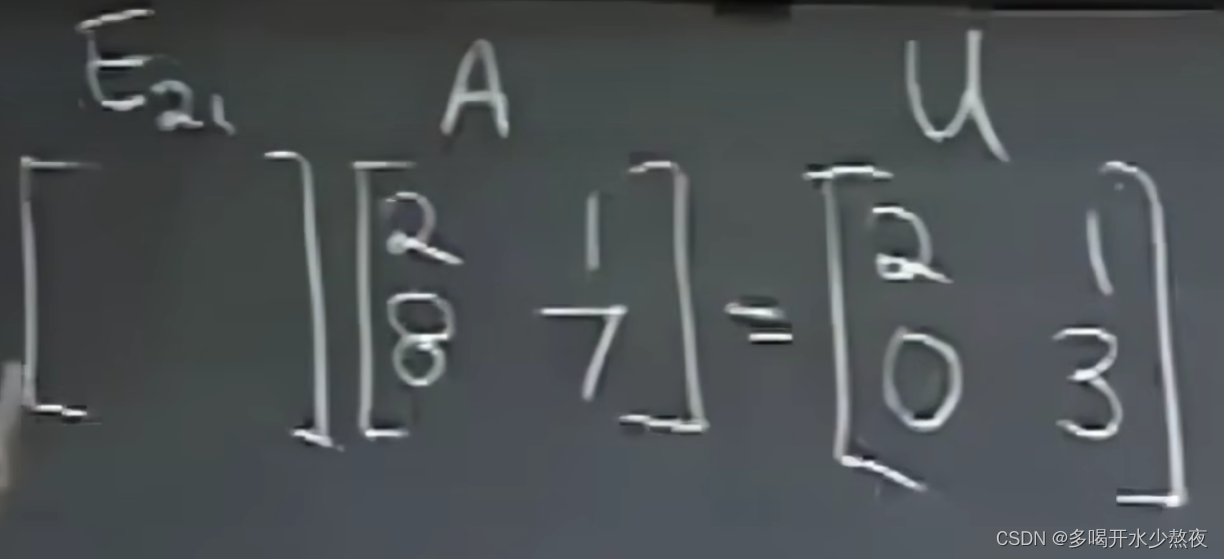
E 21 = [ 1 0 − 4 1 ] E_{21}=\begin{bmatrix}1 & 0 \\-4 & 1 \end{bmatrix} E21=[1−401]
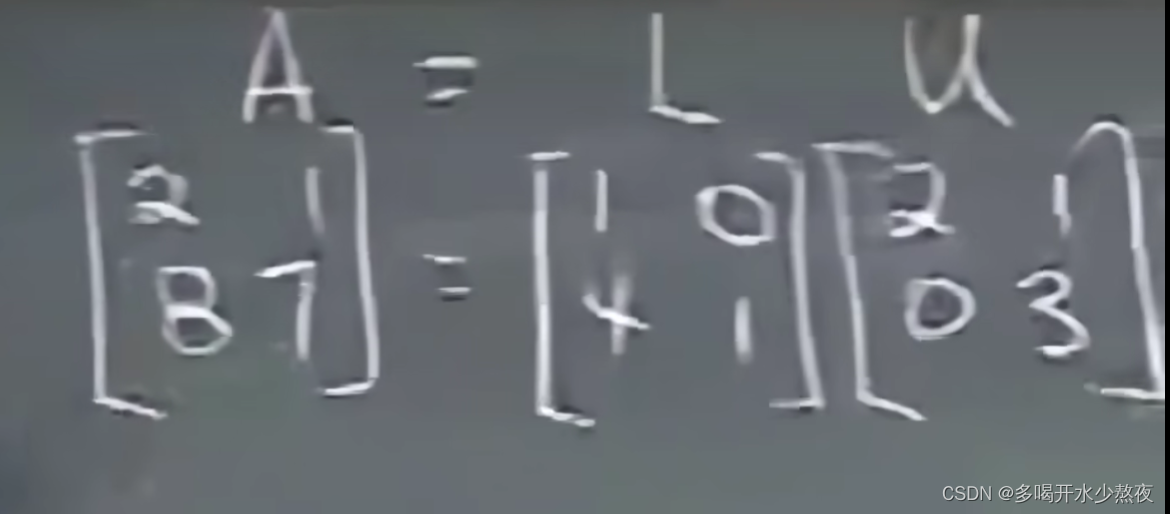
L = E 21 − 1 L=E_{21}^{-1} L=E21−1
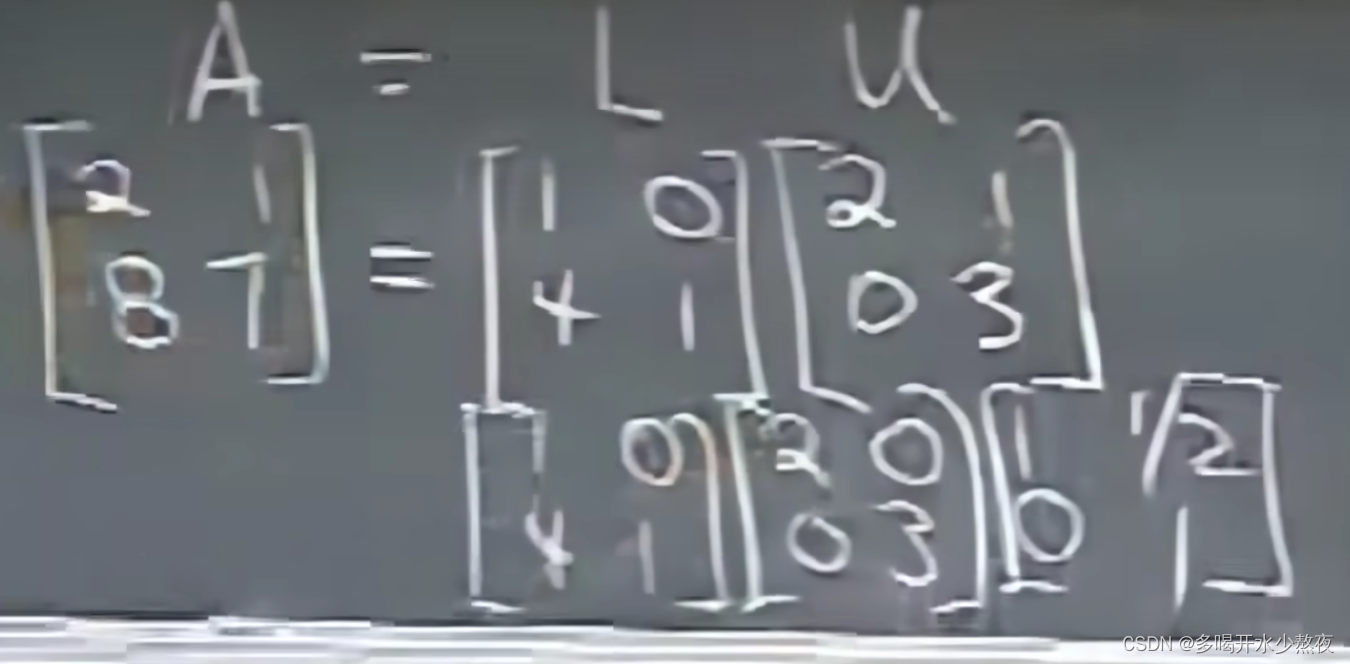
E 32 E 31 E 21 A = U ( n o r o w e x c h a n g e ) A = E 21 − 1 E 31 − 1 E 32 − 1 U E_{32}E_{31}E_{21}A=U(no{\,\,} row{\,}exchange)\\ A=E_{21}^{-1}E_{31}^{-1}E_{32}^{-1}U E32E31E21A=U(norowexchange)A=E21−1E31−1E32−1U

1 0 0 2 1 0 0 5 1 \] = L ( l e f t o f U ) E A = U A = L U \\begin{bmatrix}1 \&0 \& 0\\\\2 \& 1\&0\\\\0\&5\&1 \\end{bmatrix}=L(left{\\,}of{\\,}U)\\\\ EA=U A=LU 120015001 =L(leftofU)EA=UA=LU 原因:然而L是恢复为original矩阵的逆过程,也就是从下向上处理的,同样使用较上的行来处理较下的行,然而自下而上不会更改较上的行。 原因:E是从上向下处理的,使用较上的行来处理较下的行,然而较上的行不一定是original的,有可能是经过处理修改的。 1. L中的矩阵相乘的顺序很好,从左往右从上往下 2. 初等矩阵都是单位阵来的,对角线都是1 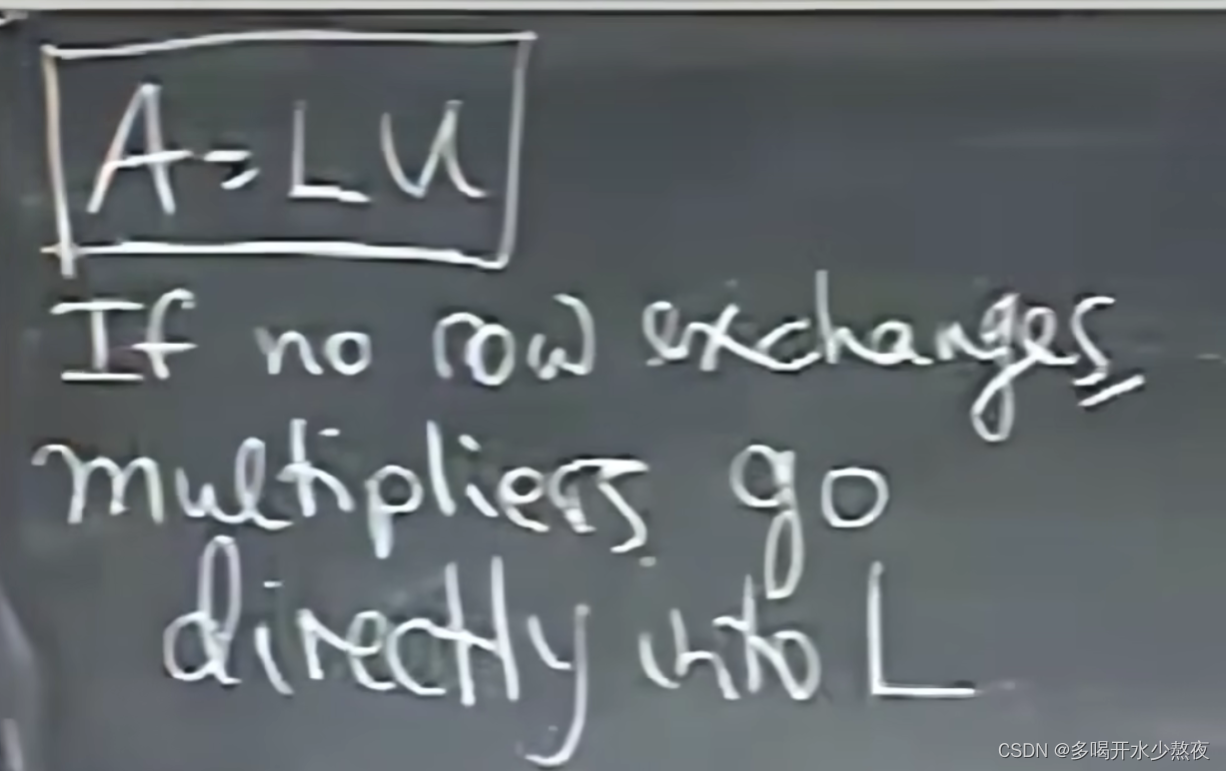 类似于时间复杂度如果n=100,对于n \* n的矩阵A需要进行多少次操作(每个元素一次乘法+一次减法进行小消元)变成下三角矩阵? 首先把矩阵留下第一行第一列的主元,第n行第一列为0,需要大约100\^2次运算 同理,把矩阵留下第二行第二列的主元,第n行第二列为0,需要大约99\^2次运算... 总操作数是:大约是 1 / 3 ∗ n 3 1/3\*n\^3 1/3∗n3的总操作次数 a l l o p r a t i o n s = n 2 + ( n − 1 ) 2 + . . . 1 2 = n ( n + 1 )( 2 n + 1 ) / 6 all{\\,}oprations=n\^2+(n-1)\^2+...1\^2=n(n+1)(2n+1)/6 alloprations=n2+(n−1)2+...12=n(n+1)(2n+1)/6  对于增广矩阵右侧的b,需要n\^2次操作次数 n \* n的矩阵有 n ! n! n!种置换矩阵 P − 1 = P T P\^{-1}=P\^{T} P−1=PT  ## 5.05转置,置换,向量空间 ### 置换 permutations P:execute row exchanges A=LU的分解其实就是L是A行变换的过程U是行变换的结果 如果要进行 行变换A=LU 就要变成PA=LU 置换矩阵是行重新排列了的单位矩阵 n \* n的矩阵有n!种置换矩阵,就是各行重新排列后所有可能的数目 P都是可逆的,并且满足以下式子 P − 1 = P T P T P = I P\^{-1}=P\^{T}\\\\ P\^{T}P=I P−1=PTPTP=I 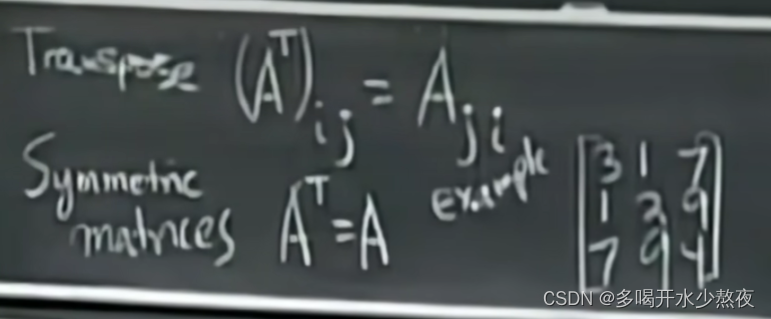 ### 转置 R\^TR 得出来的矩阵都是对称的 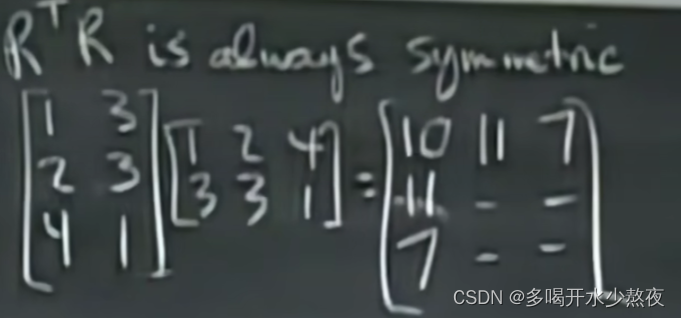 ( R T R ) T = R T R T T = R T R (R\^TR)\^T=R\^{T}R\^{TT}=R\^TR (RTR)T=RTRTT=RTR ### 向量空间  向量空间对数乘和加法两种运算(线性组合)是封闭的 子空间内必须包含0向量 二维空间的子空间是过原点的一条直线 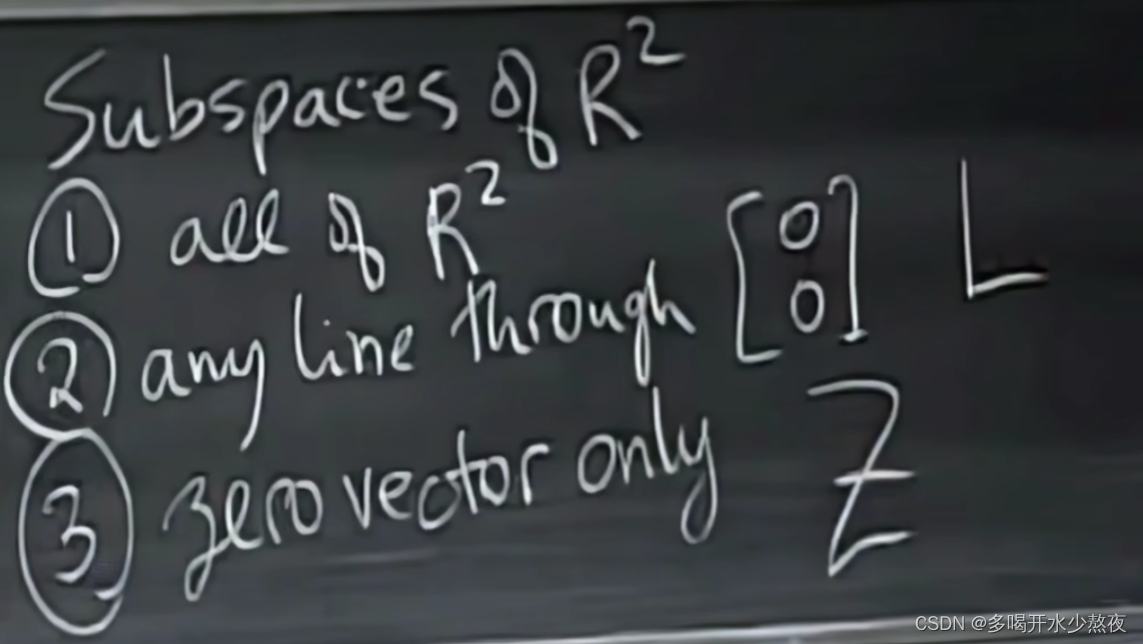  这一讲的核心思想是,通过某些向量构成一个向量组成的空间如果这些空间属于R3,那么它们构成的空间也在R3内,关键是,对其进行线性组合后仍然在子空间内 子空间:过原点、点(1,2,4)、点(3,3,1)的平面 如何构造矩阵列空间:取出每一列,线性组合,所有的线性组合就能构成列空间 ## 6.06列空间和零空间 子空间S和T的交集是一个子空间 交集必含有零向量,线与线的交集是原点,线与面的交集要么是原点要么是线本身,面与面的交集要么是一条过原点的线要么是面本身 S和T的交集取向量v和w,则v,w既属于S也属于T,而S,T中的v,w是满足"加和数乘"规则的    三个列向量的线性组合无法充满整个四维空间 那么理解:四维空间里的三个向量最多只能组成四维空间里的三维空间,而要让B有解,就必须充满四维空间才行,因为B是四维空间里任意一个向量 问题:什么b让方程组有解:Ax=b 只有b是各列的线性组合时,Ax=b才有解  对于A,去掉某一列得到同样的列空间:去掉列三,因为列一和列二的线性组合能得到列三,也就是说列三没有贡献,列一列二为主列。(同理也可以去掉列一) A的零空间是指是的Ax=0成立的向量空间 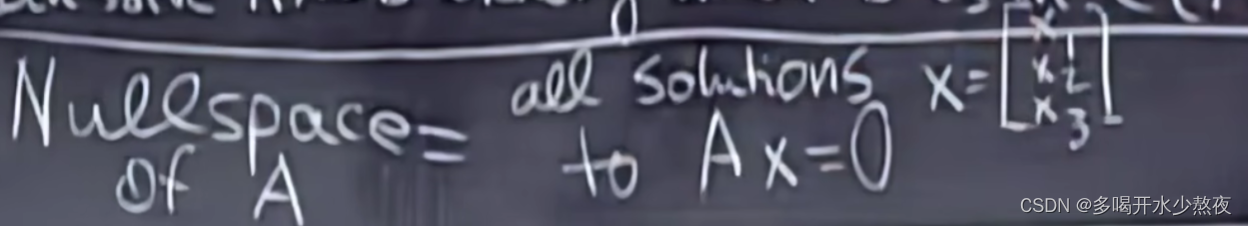  C ( A ) i n R 4 , x = \[ x 1 x 2 x 3 \] i n R 3 C(A) in R\^4, x=\\begin{bmatrix}x_1 \\\\ x_2\\\\x_3 \\end{bmatrix}in R\^3 C(A)inR4,x= x1x2x3 inR3  Ax=0包括 c \[ 1 1 − 1 \] c\\begin{bmatrix}1 \\\\ 1 \\\\-1 \\end{bmatrix} c 11−1 的一条直线 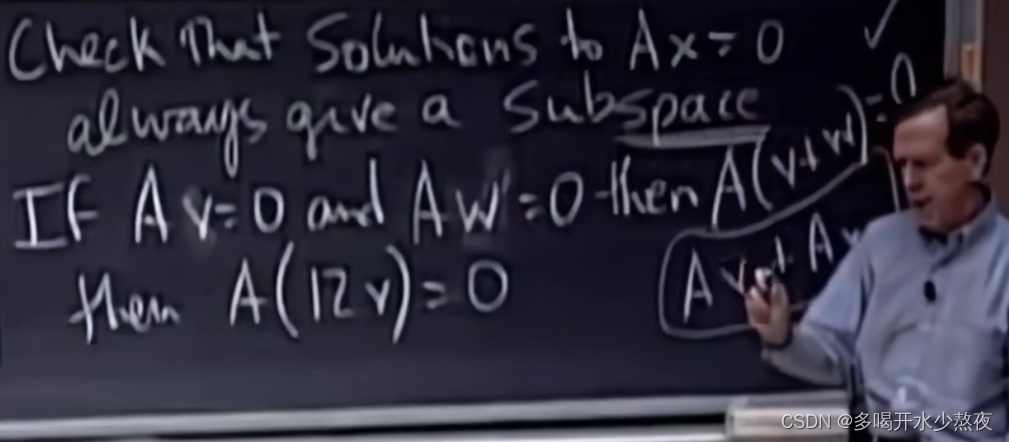 如果b不为零,Ax=b中x的解不构成子空间(0不是解),它是不过原点的一条直线。这条直线是 \[c+1, c, -c\],过(1,0,0) 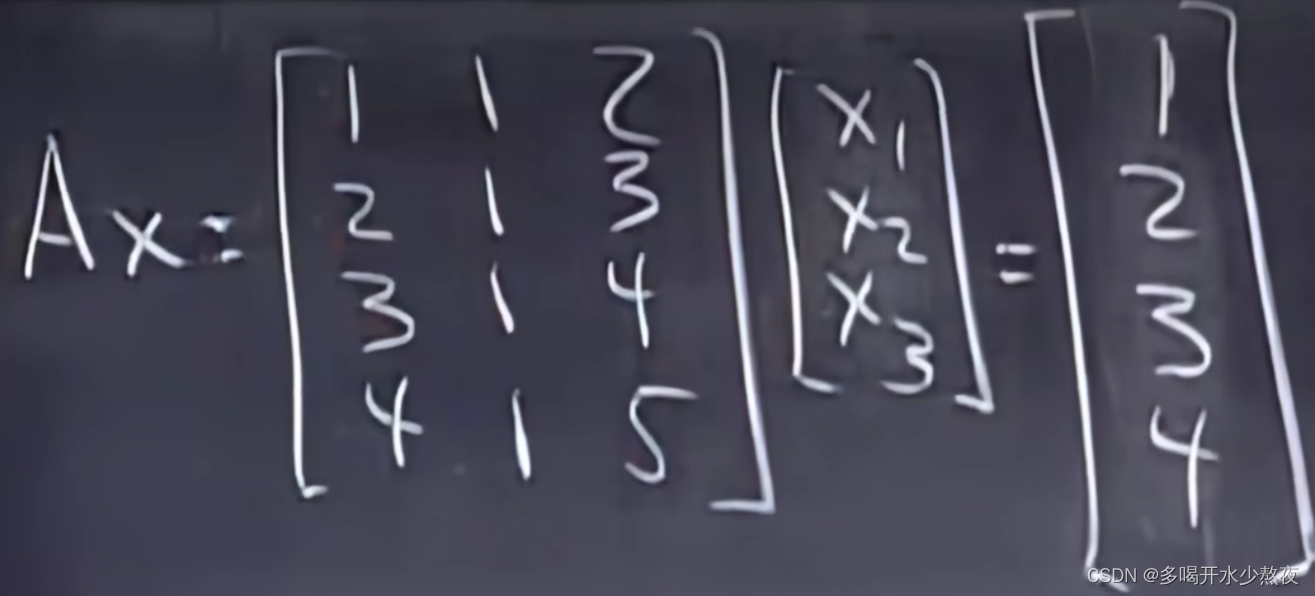 ## 7.07求解Ax=0:主变量,特解