基于树的学习算法是一种广泛而流行的非参数、有监督的分类和回归方法。
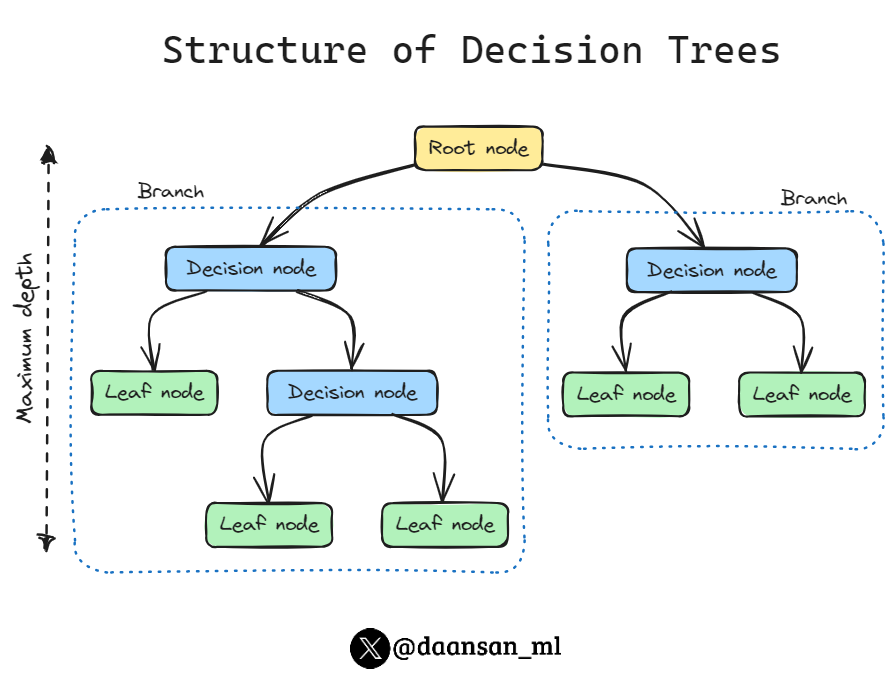
基于树的学习算法的基础是决策树(decision tree),它将一系列决策规则串联起来,看起来像一棵倒立的树,第一条决策规则位于树顶,称之为根节点(root node) 随后的决策规则分布在树下。
在决策树中,每条决策规则都出现在一个决策节点(decision node) 上,并通过该规则创建分支,通向新的节点。末端没有决策规则的分支称为叶节点(leaf) 。
机器学习模型的复杂性、知识表示的直观性各不相同,因此很难完全理解它们的工作原理。
基于树的模型的优点之一是其可解释性,决策树是一种高度直观的模型,拓展到随机森林也是如此。
1. 决策树分类器
决策树学习器试图找到一个能最大程度降低节点不纯度的决策规则。
虽然不纯度有多种测量方法,但DecisionTreeClassifier默认使用基尼不纯度(Gini impurity):
G ( t ) = 1 − ∑ i = 1 c p i 2 \begin{equation} G(t)=1-\sum_{i=1}^c{p_i}^2 \nonumber \end{equation} G(t)=1−i=1∑cpi2
其中,G(t)是节点 t 上的基尼不纯度,pi 是节点 t 上类别 c 的观测值比例。
这个寻找决策规则的过程是递归重复的,直到所有叶节点都是纯节点(即只包含一个类别)或达到某个任意的临界点。
这里以鸢尾花数据集为例,使用 scikit-learn 的DecisionTreeClassifier创建决策树分类器
# Load libraries
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
# Load data
iris = datasets.load_iris()
features = iris.data
target = iris.target
# Create decision tree classifier object
decisiontree = DecisionTreeClassifier(random_state=0)
# Train model
model = decisiontree.fit(features, target)在使用fit训练模型后,我们可以使用该模型来预测观察结果的类别:
# Make new observation
observation = [[ 5, 4, 3, 2]]
# Predict observation's class
model.predict(observation)
>>>
array([1])还可以看到观察的预测类别概率:
# View predicted class probabilities for the three classes
model.predict_proba(observation)
>>>
array([[0., 1., 0.]])最后,如果想使用不同的不纯度测量方法,可以使用criterion参数进行设置,sklearn提供了两种选择,默认采用基尼不纯度(Gini Impurity),输入'entropy'可设置为信息熵(Entropy)
# Create decision tree classifier object using entropy
decisiontree_entropy = DecisionTreeClassifier( criterion='entropy', random_state=0)
# Train model
model_entropy = decisiontree_entropy.fit(features, target)决策树可以通过将特征空间划分为矩形来建立复杂的决策边界。决策树越深,决策边界就越复杂,这很容易导致过拟合。
决策树的典型轴平行决策边界如图所示(鸢尾花数据集):

2. 决策树回归器
决策树回归的工作原理与决策树分类类似;不过,默认情况下,潜在拆分的衡量标准不是减少基尼不纯度(Gini impurity)或信息熵(entropy),而是减少均方误差(MSE)的程度:
M S E = 1 n ∑ i = 1 n ( y i − y ˉ i ) 2 \mathrm{MSE}=\frac{1}{n}\sum\limits_{i=1}^n\left(y_i-\bar{y}_i\right)^2 MSE=n1i=1∑n(yi−yˉi)2
其中, y i {y}{i} yi是目标的真实值, y ˉ i \bar{y}{i} yˉi是平均值。
在 scikit-learn 中,可以使用DecisionTreeRegressor实现决策树回归。训练好决策树后,我们就可以用它来预测观测值的目标值:
# Load libraries
from sklearn.tree import DecisionTreeRegressor
from sklearn import datasets
# Load data with only two features
diabetes = datasets.load_diabetes()
features = diabetes.data
target = diabetes.target
# Create decision tree regressor object
decisiontree = DecisionTreeRegressor(random_state=0)
# Train model
model = decisiontree.fit(features, target)
# Make new observation
observation = [features[0]]
# Predict observation's value
model.predict(observation)
>>>
array([151.])就像使用决策树分类器一样,我们可以使用criterion参数来选择所需的拆分质量方法。
例如构建一棵能减少平均绝对误差(MAE)的分割树:
# Create decision tree classifier object using MAE
decisiontree_mae = DecisionTreeRegressor(criterion="absolute_error", random_state=0)
# Train model
model_mae = decisiontree_mae.fit(features, target)3. 决策树模型的可视化
决策树分类器的优势之一是我们可以将整个训练好的模型可视化,这使得决策树成为机器学习中最易解释的模型之一。
通过tree.plot_tree可以将生成的决策树的图像,需要注意的是默认设置下分辨率较低,需要配合matplotlib进行调整
# Load libraries
from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
import matplotlib.pyplot as plt
# Load data
iris = datasets.load_iris()
features = iris.data
target = iris.target
# Create decision tree classifier object
decisiontree = DecisionTreeClassifier(random_state=0)
# Train model
model = decisiontree.fit(features, target)
# Draw tree plot
tree.plot_tree(model, feature_names= iris.feature_names, filled=True, fontsize=4)
fig = plt.gcf()
fig.dpi = 300
plt.show()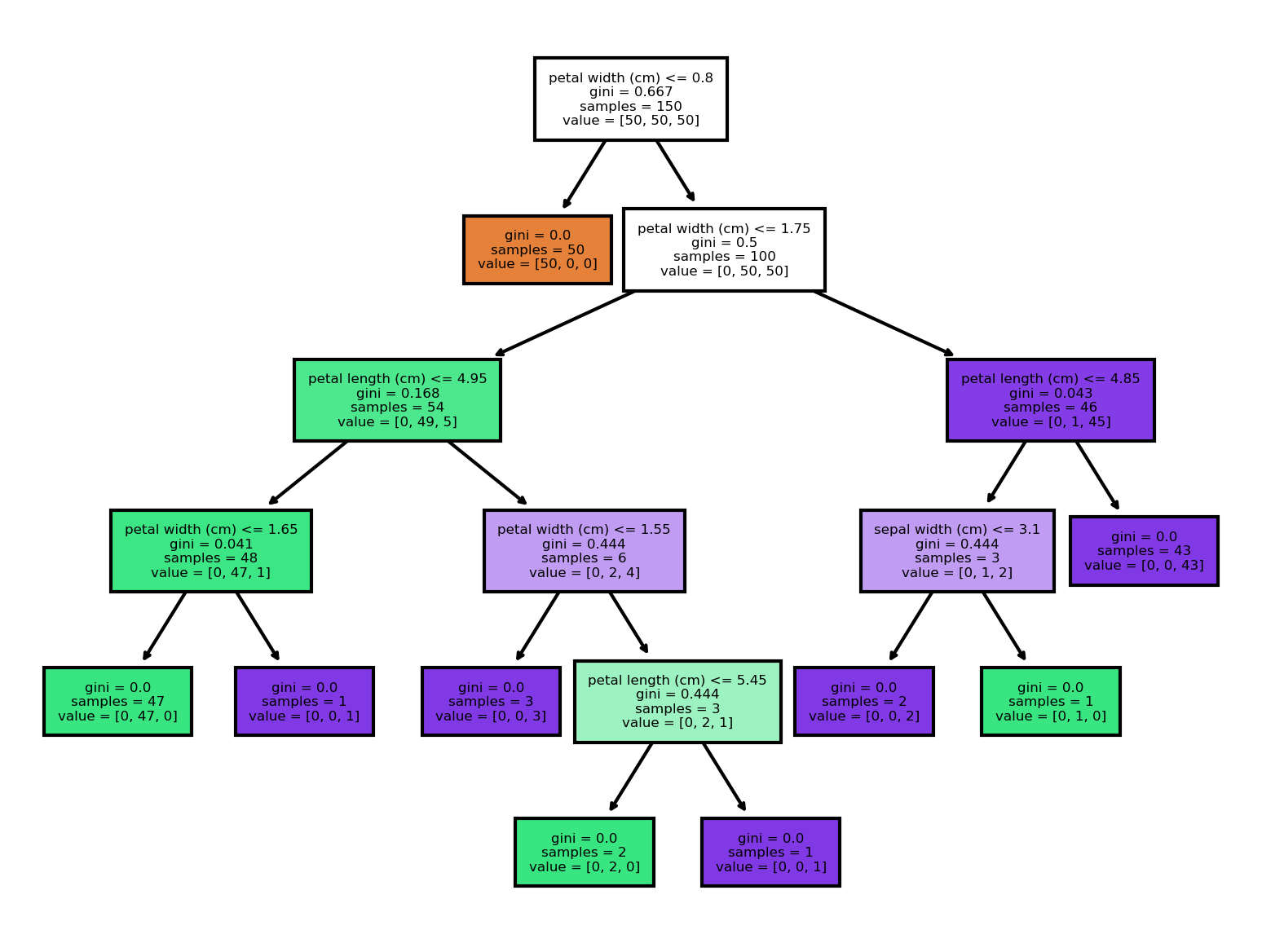
如果我们查看根节点,可以看到决策规则是:如果花瓣宽度小于或等于 0.8 厘米,则转到左分支;如果不小于或等于 0.8 厘米,则转到右分支。
还显示了基尼不纯度指数(0.667)、观测值数量(150)、每个类别中的观测值数量([50,50,50]),以及如果我们在该节点停止观测,观测值将被预测为哪个类别(setosa)。
在该节点上,学习器发现一条决策规则(花瓣宽度(厘米)<= 0.8)就能完美地识别出所有 setosa 类别的观察结果。
此外,再使用一条具有相同特征的判定规则(花瓣宽度(厘米)<= 1.75),决策树就能将 150 个观察结果中的 144 个正确分类。这说明花瓣宽度是一个非常重要的特征。
4. 随机森林
决策树的一个常见问题是,它们往往过于贴近训练数据(即过度拟合)。这催生出了称为随机森林的集合学习方法。
随机森林可视为决策树的集合,背后的理念是将存在高方差的多个(深层的)决策树平均化,从而建立一个更稳健的模型,该模型具有更好的泛化性能,并且不易过度拟合。
使用scikit-learn的RandomForestClassifier训练随机森林分类模型:
# Load libraries
from sklearn.ensemble import RandomForestClassifier
from sklearn import datasets
# Load data
iris = datasets.load_iris()
features = iris.data
target = iris.target
# Create random forest classifier object
randomforest = RandomForestClassifier(random_state=0, n_jobs=-1)
# Train model
model = randomforest.fit(features, target)使用 scikit-learn 的RandomForestRegressor训练随机森林回归模型:
# Load libraries
from sklearn.ensemble import RandomForestRegressor
from sklearn import datasets
# Load data with only two features
diabetes = datasets.load_diabetes()
features = diabetes.data
target = diabetes.target
# Create random forest regressor object
randomforest = RandomForestRegressor(random_state=0, n_jobs=-1)
# Train model
model = randomforest.fit(features, target)虽然随机森林的可解释性不如决策树,但随机森林的一大优势在于,我们不必过于担心如何选择好的超参数值。我们通常不需要对随机森林进行修剪,因为集合模型对单个决策树的平均预测噪声具有很强的鲁棒性。
在实践中,我们唯一需要关注的参数是为随机森林选择的决策树数量 k。通常情况下,树的数量越多,随机森林分类器的性能就越好,但代价是计算成本的增加。
随机森林模型与前文介绍决策树模型的十分相似,它们使用了许多相同的参数,例如,我们可以更改所使用的分割质量的方法:
# Create random forest classifier object using entropy
randomforest_entropy = RandomForestClassifier( criterion="entropy", random_state=0)
# Train model
model_entropy = randomforest_entropy.fit(features, target)不过,作为一个森林而不是一棵单独的决策树,随机森林模型也有一些独有的参数:
-
max_features参数决定了每个节点要考虑的最大特征数,它可以接受多个参数,包括整数(特征数)、浮点数(特征百分比)和 sqrt(特征数的平方根)。默认情况下max_features为auto,其作用与 sqrt 相同。 -
bootstrap参数设置在构建树时是否使用bootstrap采样(默认为True)。Bootstrap是一种随机抽样方法,它的核心思想是通过多次从原始数据集中随机抽取子集来生成多个训练集,然后使用这些训练集来训练多个决策树,否则对每一个决策树都使用所有的数据集进行训练。 -
n_estimators参数用于设置森林中决策树的数量。
顺便一提,由于训练随机森林模型实际上相当于训练许多决策树模型,因此如上述代码所示,设置 n_jobs=-1 来使用所有可用核心可有效提升效率。
5. 识别重要特征
决策树的主要优点之一是可解释性,就像第3节所介绍的一样,我们可以将整个模型可视化。
然而,随机森林模型是由数十、数百甚至数千个决策树组成的,因此对随机森林模型进行简单、直观的可视化是不切实际的。
尽管如此,这里还有另一种选择:我们可以比较(并可视化)每个特征的相对重要性。
在第3节中,我们对决策树分类器模型进行了可视化,发现仅基于花瓣宽度的决策规则就能对许多观察结果进行正确分类。这意味着花瓣宽度是分类器中的一个重要特征,也就是说不纯度(例如分类器中的基尼不纯度或熵以及回归因子中的方差)平均下降幅度越大的分裂特征就越重要。
不过,在特征重要性方面有两点需要注意:
- scikit-learn 要求我们将名义分类特征分解成多个二元特征。这样做的结果是将该特征的重要性分散到所有二元特征中,即使原始的名义分类特征非常重要,也会使每个特征看起来不重要。
- 如果两个特征高度相关,其中一个特征就会占据大部分重要性,使另一个特征显得不那么重要,如果不考虑这一点,就会对解释产生影响。
在 scikit-learn 中,分类和回归决策树以及随机森林可以使用feature_importances_方法报告每个特征的相对重要性:
# Load libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
from sklearn import datasets
# Load data
iris = datasets.load_iris()
features = iris.data
target = iris.target
# Create random forest classifier object
randomforest = RandomForestClassifier(random_state=0, n_jobs=-1)
# Train model
model = randomforest.fit(features, target)
# Calculate feature importances
importances = model.feature_importances_
# Sort feature importances in descending order
indices = np.argsort(importances)[::-1]
# Rearrange feature names so they match the sorted feature importances
names = [iris.feature_names[i] for i in indices]
# Create plot
plt.figure()
# Create plot title
plt.title("Feature Importance")
# Add bars
plt.bar(range(features.shape[1]), importances[indices])
# Add feature names as x-axis labels
plt.xticks(range(features.shape[1]), names, rotation=90)
# Show plot
plt.show()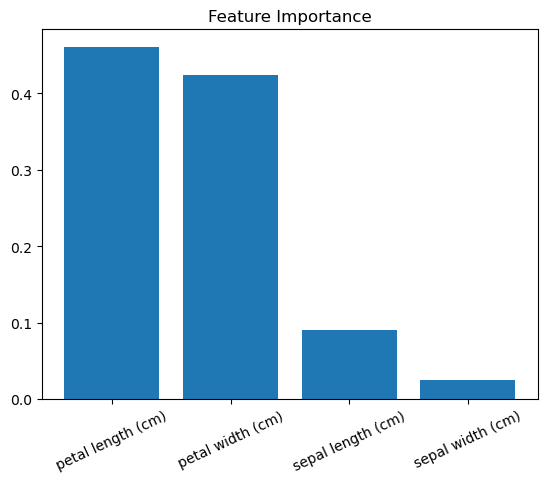
结果数值越大,该功能越重要(所有重要性分数总和为 1)。
通过绘制特征重要性数据图,可以增加随机森林模型的可解释性。