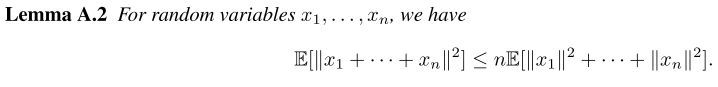
一、知识联系:随机变量和的范数平方的期望不会超过单个随机变量范数平方期望之和的n倍,是对"和的平方不超过平方和的n倍"这一初等不等式在随机变量情形下的推广。
-
初等不等式回顾:
- 对于实数 x 1 , x 2 , ... , x n x_1, x_2, \dots, x_n x1,x2,...,xn,有初等不等式:
( ∑ i = 1 n x i ) 2 ≤ n ∑ i = 1 n x i 2 \left(\sum_{i=1}^n x_i\right)^2 \leq n \sum_{i=1}^n x_i^2 (i=1∑nxi)2≤ni=1∑nxi2
这是柯西-施瓦茨不等式的特例,表明"和的平方不超过平方和的n倍"。
- 对于实数 x 1 , x 2 , ... , x n x_1, x_2, \dots, x_n x1,x2,...,xn,有初等不等式:
-
随机变量推广:
- 对于随机变量 X 1 , X 2 , ... , X n X_1, X_2, \dots, X_n X1,X2,...,Xn,其推广形式为:
E [ ∥ ∑ i = 1 n X i ∥ 2 ] ≤ n ∑ i = 1 n E [ ∥ X i ∥ 2 ] \mathbb{E}\left[\left\|\sum_{i=1}^n X_i\right\|^2\right] \leq n \sum_{i=1}^n \mathbb{E}\left[\|X_i\|^2\right] E i=1∑nXi 2 ≤ni=1∑nE[∥Xi∥2]
其中 ∥ ⋅ ∥ \|\cdot\| ∥⋅∥表示范数(如欧几里得范数), E \mathbb{E} E表示期望。
- 对于随机变量 X 1 , X 2 , ... , X n X_1, X_2, \dots, X_n X1,X2,...,Xn,其推广形式为:
-
正确性条件:
- 该不等式成立需要满足:
- 所有随机变量的二阶矩存在(即 E [ ∥ X i ∥ 2 ] < ∞ \mathbb{E}[\|X_i\|^2] < \infty E[∥Xi∥2]<∞)
- 范数平方的期望满足线性性质
- 对于独立随机变量,该不等式严格成立;对于相关随机变量,可能需要额外条件
- 该不等式成立需要满足:
-
数学本质:
- 这是将确定性变量的不等式通过期望运算推广到随机变量情形
- 核心思想是通过期望的线性性保持不等式结构
- 系数n的保留源于初等不等式中的维度因素
二、引理证明
要证明引理 Lemma A.2 :对于随机变量 x 1 , x 2 , ... , x n x_1, x_2, \ldots, x_n x1,x2,...,xn,有 E [ ∥ x 1 + x 2 + ⋯ + x n ∥ 2 ] ≤ n ( E [ ∥ x 1 ∥ 2 ] + E [ ∥ x 2 ∥ 2 ] + ⋯ + E [ ∥ x n ∥ 2 ] ) \mathbb{E}\left[\left\|x_1 + x_2 + \cdots + x_n\right\|^2\right] \leq n\left(\mathbb{E}\left[\left\|x_1\right\|^2\right] + \mathbb{E}\left[\left\|x_2\right\|^2\right] + \cdots + \mathbb{E}\left[\left\|x_n\right\|^2\right]\right) E[∥x1+x2+⋯+xn∥2]≤n(E[∥x1∥2]+E[∥x2∥2]+⋯+E[∥xn∥2]),步骤如下:
步骤1:展开范数平方
对随机变量和的范数平方利用内积性质展开:
∥ x 1 + x 2 + ⋯ + x n ∥ 2 = ⟨ ∑ i = 1 n x i , ∑ j = 1 n x j ⟩ = ∑ i = 1 n ∥ x i ∥ 2 + 2 ∑ 1 ≤ i < j ≤ n ⟨ x i , x j ⟩ \left\|x_1 + x_2 + \cdots + x_n\right\|^2 = \left\langle \sum_{i=1}^n x_i, \sum_{j=1}^n x_j \right\rangle = \sum_{i=1}^n \left\|x_i\right\|^2 + 2\sum_{1 \leq i < j \leq n} \left\langle x_i, x_j \right\rangle ∥x1+x2+⋯+xn∥2=⟨i=1∑nxi,j=1∑nxj⟩=i=1∑n∥xi∥2+21≤i<j≤n∑⟨xi,xj⟩
其中 ⟨ x i , x j ⟩ \left\langle x_i, x_j \right\rangle ⟨xi,xj⟩为 x i x_i xi与 x j x_j xj的内积, ∥ x i ∥ 2 = ⟨ x i , x i ⟩ \left\|x_i\right\|^2 = \left\langle x_i, x_i \right\rangle ∥xi∥2=⟨xi,xi⟩为范数平方。
步骤2:取期望并拆分交叉项
对等式两边取期望,利用期望的线性性质:
E [ ∥ x 1 + ⋯ + x n ∥ 2 ] = ∑ i = 1 n E [ ∥ x i ∥ 2 ] + 2 ∑ 1 ≤ i < j ≤ n E [ ⟨ x i , x j ⟩ ] \mathbb{E}\left[\left\|x_1 + \cdots + x_n\right\|^2\right] = \sum_{i=1}^n \mathbb{E}\left[\left\|x_i\right\|^2\right] + 2\sum_{1 \leq i < j \leq n} \mathbb{E}\left[\left\langle x_i, x_j \right\rangle\right] E[∥x1+⋯+xn∥2]=i=1∑nE[∥xi∥2]+21≤i<j≤n∑E[⟨xi,xj⟩]
记第一项为主对角线项 ,第二项为交叉项。
步骤3:交叉项的放缩
对交叉项 E [ ⟨ x i , x j ⟩ ] \mathbb{E}\left[\left\langle x_i, x_j \right\rangle\right] E[⟨xi,xj⟩],利用以下不等式:
- 柯西-施瓦茨不等式 : ∣ ⟨ x i , x j ⟩ ∣ ≤ ∥ x i ∥ ∥ x j ∥ \left|\left\langle x_i, x_j \right\rangle\right| \leq \left\|x_i\right\| \left\|x_j\right\| ∣⟨xi,xj⟩∣≤∥xi∥∥xj∥,两边取期望得:
∣ E [ ⟨ x i , x j ⟩ ] ∣ ≤ E [ ∥ x i ∥ ∥ x j ∥ ] \left| \mathbb{E}\left[\left\langle x_i, x_j \right\rangle\right] \right| \leq \mathbb{E}\left[\left\|x_i\right\| \left\|x_j\right\|\right] ∣E[⟨xi,xj⟩]∣≤E[∥xi∥∥xj∥] - 基本不等式 :对非负随机变量 ∥ x i ∥ \left\|x_i\right\| ∥xi∥和 ∥ x j ∥ \left\|x_j\right\| ∥xj∥,有 ∥ x i ∥ ∥ x j ∥ ≤ 1 2 ( ∥ x i ∥ 2 + ∥ x j ∥ 2 ) \left\|x_i\right\| \left\|x_j\right\| \leq \frac{1}{2}\left(\left\|x_i\right\|^2 + \left\|x_j\right\|^2\right) ∥xi∥∥xj∥≤21(∥xi∥2+∥xj∥2),两边取期望得:
E [ ∥ x i ∥ ∥ x j ∥ ] ≤ 1 2 ( E [ ∥ x i ∥ 2 ] + E [ ∥ x j ∥ 2 ] ) \mathbb{E}\left[\left\|x_i\right\| \left\|x_j\right\|\right] \leq \frac{1}{2}\left(\mathbb{E}\left[\left\|x_i\right\|^2\right] + \mathbb{E}\left[\left\|x_j\right\|^2\right]\right) E[∥xi∥∥xj∥]≤21(E[∥xi∥2]+E[∥xj∥2])
步骤4:交叉项总和的上界
交叉项共有 ( n 2 ) = n ( n − 1 ) 2 \binom{n}{2} = \frac{n(n-1)}{2} (2n)=2n(n−1)项,每项满足上述放缩。因此:
2 ∑ 1 ≤ i < j ≤ n E [ ⟨ x i , x j ⟩ ] ≤ 2 ⋅ n ( n − 1 ) 2 ⋅ 1 2 ∑ i = 1 n E [ ∥ x i ∥ 2 ] 2\sum_{1 \leq i < j \leq n} \mathbb{E}\left[\left\langle x_i, x_j \right\rangle\right] \leq 2 \cdot \frac{n(n-1)}{2} \cdot \frac{1}{2} \sum_{i=1}^n \mathbb{E}\left[\left\|x_i\right\|^2\right] 21≤i<j≤n∑E[⟨xi,xj⟩]≤2⋅2n(n−1)⋅21i=1∑nE[∥xi∥2]
化简得:
2 ∑ i < j E [ ⟨ x i , x j ⟩ ] ≤ ( n − 1 ) ∑ i = 1 n E [ ∥ x i ∥ 2 ] 2\sum_{i < j} \mathbb{E}\left[\left\langle x_i, x_j \right\rangle\right] \leq (n-1) \sum_{i=1}^n \mathbb{E}\left[\left\|x_i\right\|^2\right] 2i<j∑E[⟨xi,xj⟩]≤(n−1)i=1∑nE[∥xi∥2]
步骤5:合并主对角线项与交叉项
将主对角线项与交叉项的放缩结果相加:
E [ ∥ x 1 + ⋯ + x n ∥ 2 ] ≤ ∑ i = 1 n E [ ∥ x i ∥ 2 ] + ( n − 1 ) ∑ i = 1 n E [ ∥ x i ∥ 2 ] = n ∑ i = 1 n E [ ∥ x i ∥ 2 ] \mathbb{E}\left[\left\|x_1 + \cdots + x_n\right\|^2\right] \leq \sum_{i=1}^n \mathbb{E}\left[\left\|x_i\right\|^2\right] + (n-1)\sum_{i=1}^n \mathbb{E}\left[\left\|x_i\right\|^2\right] = n \sum_{i=1}^n \mathbb{E}\left[\left\|x_i\right\|^2\right] E[∥x1+⋯+xn∥2]≤i=1∑nE[∥xi∥2]+(n−1)i=1∑nE[∥xi∥2]=ni=1∑nE[∥xi∥2]
核心思想
通过范数平方展开和内积性质,将随机变量和的二阶矩分解为主对角线项与交叉项,利用柯西-施瓦茨不等式和基本不等式对交叉项放缩,最终得到和的二阶矩关于各变量二阶矩的上界。此引理无需假设随机变量独立,是控制随机变量和二阶矩的基础工具。
总结
引理 Lemma A.2 的详细证明如下:
- 展开范数平方 :利用内积性质将 ∥ x 1 + ⋯ + x n ∥ 2 \left\|x_1+\cdots+x_n\right\|^2 ∥x1+⋯+xn∥2展开为主对角线项与交叉项之和;
- 取期望拆分:对展开式取期望,分离主对角线项和交叉项;
- 交叉项放缩:通过柯西-施瓦茨不等式和基本不等式,将交叉项放缩为各变量范数平方期望的线性组合;
- 合并结果 :主对角线项与放缩后的交叉项相加,得到 E [ ∥ x 1 + ⋯ + x n ∥ 2 ] ≤ n ∑ i = 1 n E [ ∥ x i ∥ 2 ] \mathbb{E}\left[\left\|x_1+\cdots+x_n\right\|^2\right] \leq n\sum_{i=1}^n \mathbb{E}\left[\left\|x_i\right\|^2\right] E[∥x1+⋯+xn∥2]≤n∑i=1nE[∥xi∥2]。
该引理通过控制交叉项,建立了随机变量和的二阶矩与各变量二阶矩的关系,是概率论中二阶矩估计的基础工具。