一、带正则化的成本函数（Regularized Cost Function）
1. 引入正则化的动机
在多特征模型中（例如多项式回归），当特征数量较多时，模型容易过拟合（Overfitting） 。为此我们可以在代价函数中加入一个正则化项（Regularization Term），用于"惩罚"过大的参数，使模型更加平滑、泛化性更强。
2. 带正则化的代价函数定义
假设线性回归的原始代价函数为：
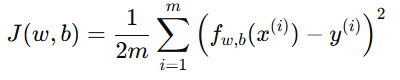
为了避免权重 wj 过大，我们添加一个正则化项：
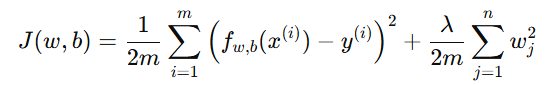
其中：
-
λ：正则化参数（Regularization Parameter）
-
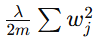：惩罚项（Penalty Term）
注意：偏置项 b 不参与正则化。
3. λ（正则化参数）的影响
-
当 λ=0：无正则化，模型可能过拟合。
-
当 λ 过大：参数被压得过小，模型可能欠拟合。
-
选择合适的 λ 可以平衡偏差与方差（Bias--Variance Tradeoff）。
二、正则化线性回归（Regularized Linear Regression）
1. 梯度下降算法的正则化更新
带正则化的代价函数对应的梯度下降更新公式为：
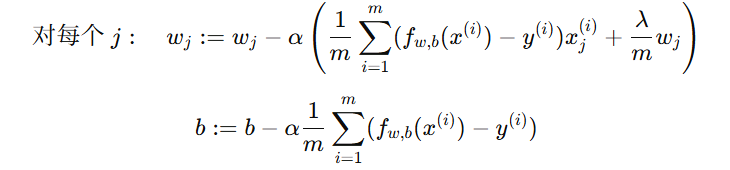
解释：
-
第一部分：普通的梯度下降更新。
-
第二部分：
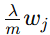是正则化项，会让参数 
缩小。
2. 推导思路（简要）
从代价函数对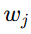 
求偏导：
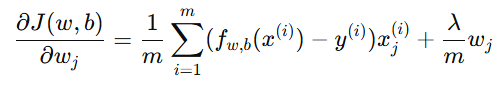
然后按梯度下降规则更新参数：
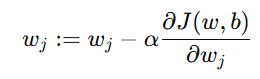
由此得到上面的更新公式。
三、正则化逻辑回归（Regularized Logistic Regression）
1. 更新逻辑回归的代价函数
逻辑回归的原始代价函数为：
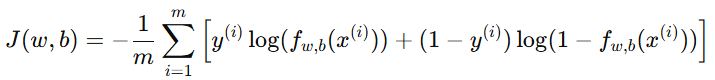
其中：
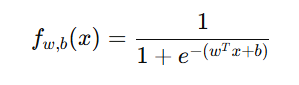
加上正则化项后：
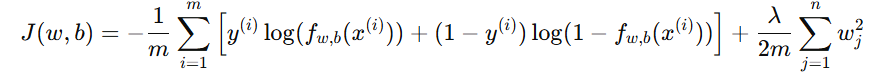
2. 正则化逻辑回归的梯度下降
对每个参数求偏导，得到更新公式：
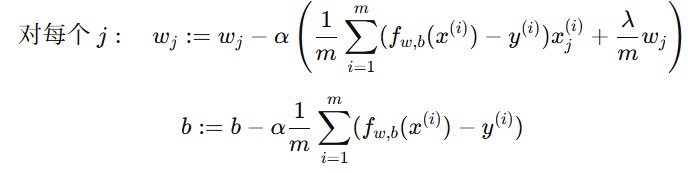
与线性回归的区别在于：
-
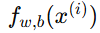为 sigmoid 函数输出； -
代价函数使用对数损失；
-
更新逻辑相同。
四、总结（Summary）
| 项目 | 线性回归 | 逻辑回归 |
|---|---|---|
| 原代价函数 | 平方误差  |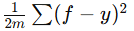
对数损失 |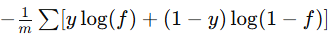
| 正则化项 |  |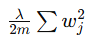
 |
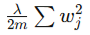| 更新规则 |  |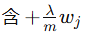
 |
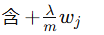| 偏置项 b | 不参与正则化 | 不参与正则化 |
| 作用 | 减小参数，防止过拟合 | 减小参数，防止过拟合 |
五、例子说明
假设我们要预测房价，模型如下：
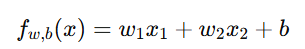
其中：
-
x1：房屋面积
-
x2：房龄
如果模型过拟合，说明参数 w1,w2 过大。使用正则化后，代价函数变为：
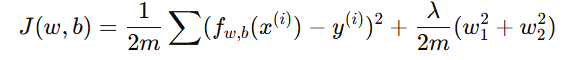
随着训练进行，较大的 w1,w2 会被"惩罚"，使模型更平滑、更稳定。