动手学深度学习——6.循环神经网络

1.序列模型

处理序列数据需要统计工具和新的深度神经网络架构。 为了简单起见，我们以 图8.1.1所示的股票价格（富时100指数）为例。

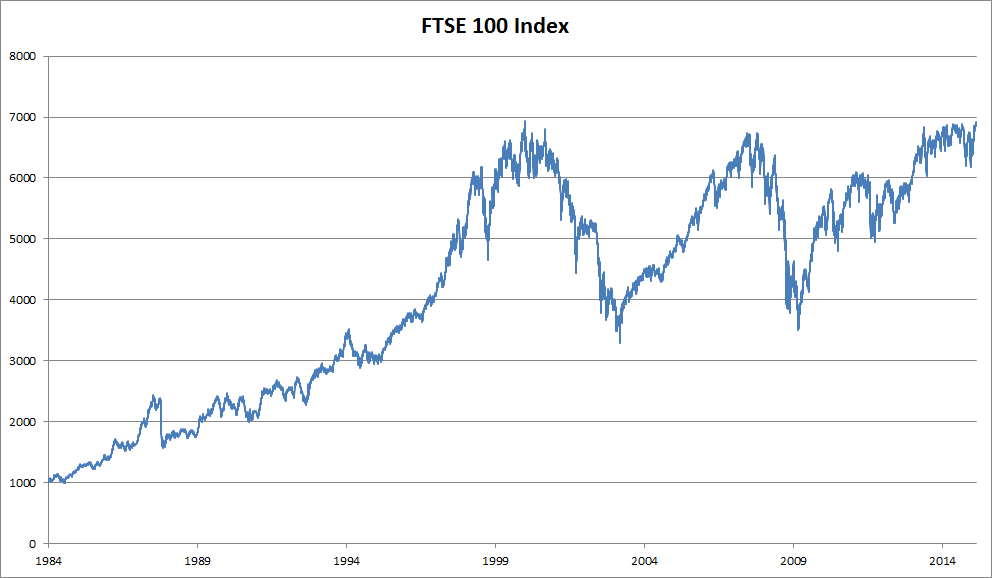
图8.1.1 近30年的富时100指数

其中，用𝑥𝑡表示价格，即在时间步（time step） 𝑡∈𝑍+时，观察到的价格𝑥𝑡。 请注意，𝑡对于本文中的序列通常是离散的，并在整数或其子集上变化。 假设一个交易员想在𝑡日的股市中表现良好，于是通过以下途径预测𝑥𝑡：

为了实现这个预测，交易员可以使用回归模型， 例如在 3.3节中训练的模型。 仅有一个主要问题：输入数据的数量， 输入𝑥𝑡−1,...,𝑥1本身因𝑡而异。 也就是说，输入数据的数量这个数字将会随着我们遇到的数据量的增加而增加， 因此需要一个近似方法来使这个计算变得容易处理。 本章后面的大部分内容将围绕着如何有效估计 𝑃(𝑥𝑡∣𝑥𝑡−1,...,𝑥1)展开。 简单地说，它归结为以下两种策略。

第一种策略，假设在现实情况下相当长的序列 𝑥𝑡−1,...,𝑥1可能是不必要的， 因此我们只需要满足某个长度为𝜏的时间跨度， 即使用观测序列𝑥𝑡−1,...,𝑥𝑡−𝜏。 当下获得的最直接的好处就是参数的数量总是不变的， 至少在𝑡>𝜏时如此，这就使我们能够训练一个上面提及的深度网络。 这种模型被称为自回归模型（autoregressive models）， 因为它们是对自己执行回归。

第二种策略 ，如 图8.1.2所示， 是保留一些对过去观测的总结ℎ𝑡， 并且同时更新预测𝑥^𝑡和总结ℎ𝑡。 这就产生了基于𝑥^𝑡=𝑃(𝑥𝑡∣ℎ𝑡)估计𝑥𝑡， 以及公式ℎ𝑡=𝑔(ℎ𝑡−1,𝑥𝑡−1)更新的模型。 由于ℎ𝑡从未被观测到，这类模型也被称为 隐变量自回归模型（latent autoregressive models）。

小结

• 内插法（在现有观测值之间进行估计）和外推法（对超出已知观测范围进行预测，换句话说，我们必须使用我们自己的预测（而不是原始数据）来进行多步预测）在实践的难度上差别很大。因此，对于所拥有的序列数据，在训练时始终要尊重其时间顺序，即最好不要基于未来的数据进行训练。

• 序列模型的估计需要专门的统计工具，两种较流行的选择是自回归模型和隐变量自回归模型。

• 对于时间是向前推进的因果模型，正向估计通常比反向估计更容易。

• 对于直到时间步𝑡的观测序列，其在时间步𝑡+𝑘的预测输出是"𝑘步预测"。随着我们对预测时间𝑘值的增加，会造成误差的快速累积和预测质量的极速下降。

2.文本预处理

对于序列数据处理问题，我们在 8.1节中 评估了所需的统计工具和预测时面临的挑战。 这样的数据存在许多种形式，文本是最常见例子之一。 例如，一篇文章可以被简单地看作一串单词序列，甚至是一串字符序列。 本节中，我们将解析文本的常见预处理步骤。 这些步骤通常包括：

1. 将文本作为字符串加载到内存中。

2. 将字符串拆分为词元（如单词和字符）。

3. 建立一个词表，将拆分的词元映射到数字索引。

4. 将文本转换为数字索引序列，方便模型操作。

3.语言模型

我们了解了如何将文本数据映射为词元， 以及将这些词元可以视为一系列离散的观测，例如单词或字符。 假设长度为𝑇的文本序列中的词元依次为𝑥1,𝑥2,...,𝑥𝑇。 于是，𝑥𝑡（1≤𝑡≤𝑇） 可以被认为是文本序列在时间步𝑡处的观测或标签。 在给定这样的文本序列时，语言模型（language model）的目标是估计序列的联合概率

例如，只需要一次抽取一个词元𝑥𝑡∼𝑃(𝑥𝑡∣𝑥𝑡−1,...,𝑥1)， 一个理想的语言模型就能够基于模型本身生成自然文本。 与猴子使用打字机完全不同的是，从这样的模型中提取的文本 都将作为自然语言（例如，英语文本）来传递。 只需要基于前面的对话片断中的文本， 就足以生成一个有意义的对话。 显然，我们离设计出这样的系统还很遥远， 因为它需要"理解"文本，而不仅仅是生成语法合理的内容。

尽管如此，语言模型依然是非常有用的。 例如，短语"to recognize speech"和"to wreck a nice beach"读音上听起来非常相似。 这种相似性会导致语音识别中的歧义，但是这很容易通过语言模型来解决， 因为第二句的语义很奇怪。 同样，在文档摘要生成算法中， "狗咬人"比"人咬狗"出现的频率要高得多， 或者"我想吃奶奶"是一个相当匪夷所思的语句， 而"我想吃，奶奶"则要正常得多。

4.循环神经网络

假设我们在时间步𝑡有小批量输入𝑋𝑡∈𝑅𝑛×𝑑。 换言之，对于𝑛个序列样本的小批量， 𝑋𝑡的每一行对应于来自该序列的时间步𝑡处的一个样本。 接下来，用𝐻𝑡∈𝑅𝑛×ℎ 表示时间步𝑡的隐藏变量。 与多层感知机不同的是， 我们在这里保存了前一个时间步的隐藏变量𝐻𝑡−1， 并引入了一个新的权重参数𝑊ℎℎ∈𝑅ℎ×ℎ， 来描述如何在当前时间步中使用前一个时间步的隐藏变量。 具体地说，当前时间步隐藏变量由当前时间步的输入 与前一个时间步的隐藏变量一起计算得出：

与隐藏层相比， 循环神经网络多添加了一项 𝐻𝑡−1𝑊ℎℎ， 从而实例化了 。 从相邻时间步的隐藏变量𝐻𝑡和 𝐻𝑡−1之间的关系可知， 这些变量捕获并保留了序列直到其当前时间步的历史信息， 就如当前时间步下神经网络的状态或记忆， 因此这样的隐藏变量被称为隐状态（hidden state）。 由于在当前时间步中， 隐状态使用的定义与前一个时间步中使用的定义相同， 因此 (8.4.5)的计算是循环的 （recurrent）。 于是基于循环计算的隐状态神经网络被命名为 循环神经网络 （recurrent neural network）。 在循环神经网络中执行 (8.4.5)计算的层 称为循环层（recurrent layer）。

有许多不同的方法可以构建循环神经网络， 由 (8.4.5)定义的隐状态的循环神经网络是非常常见的一种。 对于时间步𝑡，输出层的输出类似于多层感知机中的计算：

循环神经网络的参数包括隐藏层的权重 𝑊𝑥ℎ∈𝑅𝑑×ℎ,𝑊ℎℎ∈𝑅ℎ×ℎ和偏置𝑏ℎ∈𝑅1×ℎ， 以及输出层的权重𝑊ℎ𝑞∈𝑅ℎ×𝑞 和偏置𝑏𝑞∈𝑅1×𝑞。 值得一提的是，即使在不同的时间步，循环神经网络也总是使用这些模型参数。 因此，循环神经网络的参数开销不会随着时间步的增加而增加。

上图展示了循环神经网络在三个相邻时间步的计算逻辑。 在任意时间步𝑡，隐状态的计算可以被视为：

1. 拼接当前时间步𝑡的输入𝑋𝑡和前一时间步𝑡−1的隐状态𝐻𝑡−1；

2. 将拼接的结果送入带有激活函数𝜙的全连接层。 全连接层的输出是当前时间步𝑡的隐状态𝐻𝑡。

在本例中，模型参数是𝑊𝑥ℎ和𝑊ℎℎ的拼接， 以及𝑏ℎ的偏置，所有这些参数都来自 (8.4.5)。 当前时间步𝑡的隐状态𝐻𝑡 将参与计算下一时间步𝑡+1的隐状态𝐻𝑡+1。 而且𝐻𝑡还将送入全连接输出层， 用于计算当前时间步𝑡的输出𝑂𝑡。

我们刚才提到，隐状态中 𝑋𝑡𝑊𝑥ℎ+𝐻𝑡−1𝑊ℎℎ的计算， 相当于𝑋𝑡和𝐻𝑡−1的拼接 与𝑊𝑥ℎ和𝑊ℎℎ的拼接的矩阵乘法。 虽然这个性质可以通过数学证明， 但在下面我们使用一个简单的代码来说明一下。 首先，我们定义矩阵X、W_xh、H和W_hh， 它们的形状分别为，(3，1)、，(1，4)、，(3，4)和，(4，4)。 分别将X乘以W_xh，将H乘以W_hh， 然后将这两个乘法相加，我们得到一个形状为，(3，4)的矩阵。

举例

回想一下 8.3节中的语言模型， 我们的目标是根据过去的和当前的词元预测下一个词元， 因此我们将原始序列移位一个词元作为标签。 Bengio等人首先提出使用神经网络进行语言建模 (Bengio et al., 2003)。 接下来，我们看一下如何使用循环神经网络来构建语言模型。 设小批量大小为1，批量中的文本序列为"machine"。 为了简化后续部分的训练，我们考虑使用 字符级语言模型 （character-level language model）， 将文本词元化为字符而不是单词。 图8.4.2演示了 如何通过基于字符级语言建模的循环神经网络， 使用当前的和先前的字符预测下一个字符。

在训练过程中，我们对每个时间步的输出层的输出进行softmax操作， 然后利用交叉熵损失计算模型输出和标签之间的误差。 由于隐藏层中隐状态的循环计算， 图8.4.2中的第3个时间步的输出𝑂3 由文本序列"m""a"和"c"确定。 由于训练数据中这个文本序列的下一个字符是"h"， 因此第3个时间步的损失将取决于下一个字符的概率分布， 而下一个字符是基于特征序列"m""a""c"和这个时间步的标签"h"生成的。

5.评价指标

最后，让我们讨论如何度量语言模型的质量， 这将在后续部分中用于评估基于循环神经网络的模型。 一个好的语言模型能够用高度准确的词元来预测我们接下来会看到什么。

我们可以通过计算序列的似然概率来度量模型的质量。我们在引入softmax回归 （ 3.4.7节）时定义了熵、惊异和交叉熵， 并在信息论的在线附录 中讨论了更多的信息论知识。 如果想要压缩文本，我们可以根据当前词元集预测的下一个词元。 一个更好的语言模型应该能让我们更准确地预测下一个词元。 因此，它应该允许我们在压缩序列时花费更少的比特。 所以我们可以通过一个序列中所有的𝑛个词元的交叉熵损失的平均值来衡量：

其中𝑃由语言模型给出， 𝑥𝑡是在时间步𝑡从该序列中观察到的实际词元。 这使得不同长度的文档的性能具有了可比性。 由于历史原因，自然语言处理的科学家更喜欢使用一个叫做困惑度（perplexity）的量。

困惑度的最好的理解是"下一个词元的实际选择数的调和平均数"。

6.实现循环神经网络

回想一下，在train_iter中，每个词元都表示为一个数字索引， 将这些索引直接输入神经网络可能会使学习变得困难。 我们通常将每个词元表示为更具表现力的特征向量。 最简单的表示称为独热编码（one-hot encoding）， 它在 3.4.1节中介绍过。

简言之，将每个索引映射为相互不同的单位向量： 假设词表中不同词元的数目为𝑁（即len(vocab)）， 词元索引的范围为0到𝑁−1。 如果词元的索引是整数𝑖， 那么我们将创建一个长度为𝑁的全0向量， 并将第𝑖处的元素设置为1。 此向量是原始词元的一个独热向量。

我们每次采样的小批量数据形状是二维张量： （批量大小，时间步数）。 one_hot函数将这样一个小批量数据转换成三维张量， 张量的最后一个维度等于词表大小（len(vocab)）。 我们经常转换输入的维度，以便获得形状为 （时间步数，批量大小，词表大小）的输出。 这将使我们能够更方便地通过最外层的维度， 一步一步地更新小批量数据的隐状态。

为了定义循环神经网络模型， 我们首先需要一个init_rnn_state函数在初始化时返回隐状态。 这个函数的返回是一个张量，张量全用0填充， 形状为（批量大小，隐藏单元数）。 在后面的章节中我们将会遇到隐状态包含多个变量的情况， 而使用元组可以更容易地处理些。

def rnn(inputs, state, params):
    # inputs的形状：(时间步数量，批量大小，词表大小)
    W_xh, W_hh, b_h, W_hq, b_q = params
    H, = state
    outputs = []
    # X的形状：(批量大小，词表大小)
    for X in inputs:
        H = torch.tanh(torch.mm(X, W_xh) + torch.mm(H, W_hh) + b_h)
        Y = torch.mm(H, W_hq) + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H,)

定义了所有需要的函数之后，接下来我们创建一个类来包装这些函数， 并存储从零开始实现的循环神经网络模型的参数。

class RNNModelScratch: #@save
    """从零开始实现的循环神经网络模型"""
    def __init__(self, vocab_size, num_hiddens, device,
                 get_params, init_state, forward_fn):
        self.vocab_size, self.num_hiddens = vocab_size, num_hiddens
        self.params = get_params(vocab_size, num_hiddens, device)
        self.init_state, self.forward_fn = init_state, forward_fn

    def __call__(self, X, state):
        X = F.one_hot(X.T, self.vocab_size).type(torch.float32)
        return self.forward_fn(X, state, self.params)

    def begin_state(self, batch_size, device):
        return self.init_state(batch_size, self.num_hiddens, device)

让我们检查输出是否具有正确的形状。 例如，隐状态的维数是否保持不变。

num_hiddens = 512
net = RNNModelScratch(len(vocab), num_hiddens, d2l.try_gpu(), get_params,
                      init_rnn_state, rnn)
state = net.begin_state(X.shape[0], d2l.try_gpu())
Y, new_state = net(X.to(d2l.try_gpu()), state)
Y.shape, len(new_state), new_state[0].shape

(torch.Size([10, 28]), 1, torch.Size([2, 512]))

我们可以看到输出形状是（时间步数×批量大小，词表大小）， 而隐状态形状保持不变，即（批量大小，隐藏单元数）。

7.训练模型

在训练模型之前，让我们定义一个函数在一个迭代周期内训练模型。 它与我们训练 3.6节模型的方式有三个不同之处。

1. 序列数据的不同采样方法（随机采样和顺序分区）将导致隐状态初始化的差异。

2. 我们在更新模型参数之前裁剪梯度。 这样的操作的目的是，即使训练过程中某个点上发生了梯度爆炸，也能保证模型不会发散。

3. 我们用困惑度来评价模型。如 8.4.4节所述， 这样的度量确保了不同长度的序列具有可比性。

具体来说，当使用顺序分区时， 我们只在每个迭代周期的开始位置初始化隐状态。 由于下一个小批量数据中的第𝑖个子序列样本 与当前第𝑖个子序列样本相邻， 因此当前小批量数据最后一个样本的隐状态， 将用于初始化下一个小批量数据第一个样本的隐状态。 这样，存储在隐状态中的序列的历史信息 可以在一个迭代周期内流经相邻的子序列。 然而，在任何一点隐状态的计算， 都依赖于同一迭代周期中前面所有的小批量数据， 这使得梯度计算变得复杂。 为了降低计算量，在处理任何一个小批量数据之前， 我们先分离梯度，使得隐状态的梯度计算总是限制在一个小批量数据的时间步内。

当使用随机抽样时，因为每个样本都是在一个随机位置抽样的， 因此需要为每个迭代周期重新初始化隐状态。 与 3.6节中的 train_epoch_ch3函数相同， updater是更新模型参数的常用函数。 它既可以是从头开始实现的d2l.sgd函数， 也可以是深度学习框架中内置的优化函数。

#@save
def train_epoch_ch8(net, train_iter, loss, updater, device, use_random_iter):
    """训练网络一个迭代周期（定义见第8章）"""
    state, timer = None, d2l.Timer()
    metric = d2l.Accumulator(2)  # 训练损失之和,词元数量
    for X, Y in train_iter:
        if state is None or use_random_iter:
            # 在第一次迭代或使用随机抽样时初始化state
            state = net.begin_state(batch_size=X.shape[0], device=device)
        else:
            if isinstance(net, nn.Module) and not isinstance(state, tuple):
                # state对于nn.GRU是个张量
                state.detach_()
            else:
                # state对于nn.LSTM或对于我们从零开始实现的模型是个张量
                for s in state:
                    s.detach_()
        y = Y.T.reshape(-1)
        X, y = X.to(device), y.to(device)
        y_hat, state = net(X, state)
        l = loss(y_hat, y.long()).mean()
        if isinstance(updater, torch.optim.Optimizer):
            updater.zero_grad()
            l.backward()
            grad_clipping(net, 1)
            updater.step()
        else:
            l.backward()
            grad_clipping(net, 1)
            # 因为已经调用了mean函数
            updater(batch_size=1)
        metric.add(l * y.numel(), y.numel())
    return math.exp(metric[0] / metric[1]), metric[1] / timer.stop()

循环神经网络模型的训练函数既支持从零开始实现， 也可以使用高级API来实现。

#@save
def train_ch8(net, train_iter, vocab, lr, num_epochs, device,
              use_random_iter=False):
    """训练模型（定义见第8章）"""
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', ylabel='perplexity',
                            legend=['train'], xlim=[10, num_epochs])
    # 初始化
    if isinstance(net, nn.Module):
        updater = torch.optim.SGD(net.parameters(), lr)
    else:
        updater = lambda batch_size: d2l.sgd(net.params, lr, batch_size)
    predict = lambda prefix: predict_ch8(prefix, 50, net, vocab, device)
    # 训练和预测
    for epoch in range(num_epochs):
        ppl, speed = train_epoch_ch8(
            net, train_iter, loss, updater, device, use_random_iter)
        if (epoch + 1) % 10 == 0:
            print(predict('time traveller'))
            animator.add(epoch + 1, [ppl])
    print(f'困惑度 {ppl:.1f}, {speed:.1f} 词元/秒 {str(device)}')
    print(predict('time traveller'))
    print(predict('traveller'))

现在，我们训练循环神经网络模型。 因为我们在数据集中只使用了10000个词元， 所以模型需要更多的迭代周期来更好地收敛。

num_epochs, lr = 500, 1
train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu())

困惑度 1.0, 67212.6 词元/秒 cuda:0
time traveller for so it will be convenient to speak of himwas e
travelleryou can show black is white by argument said filby

小结

• 我们可以训练一个基于循环神经网络的字符级语言模型，根据用户提供的文本的前缀生成后续文本。

• 一个简单的循环神经网络语言模型包括输入编码、循环神经网络模型和输出生成。

• 循环神经网络模型在训练以前需要初始化状态，不过随机抽样和顺序划分使用初始化方法不同。

• 当使用顺序划分时，我们需要分离梯度以减少计算量。

• 在进行任何预测之前，模型通过预热期进行自我更新（例如，获得比初始值更好的隐状态）。

• 梯度裁剪可以防止梯度爆炸，但不能应对梯度消失。