机器学习笔记

1. 监督学习（Supervised Learning）

监督学习（Supervised Learning）是机器学习的一种方法，它利用带有标签的数据来训练模型，使模型能够从输入数据中预测输出。监督学习的目标是找到一个函数或映射关系（x --> y），使得给定新的输入数据时，模型能够准确地预测对应的输出。监督学习广泛应用于各种实际问题中，如分类、回归、语音识别、图像识别等。

监督学习的主要类型

• 回归（Regression）：任务是预测连续数值输出。例如，房价预测（根据房屋特征预测其价格）、股票价格预测（根据历史数据预测未来价格）。
• 分类（ Classification）：任务是将输入数据分配到预定义的类别中。例如，垃圾邮件分类（将邮件分类为"垃圾邮件"或"非垃圾邮件"）、图像分类（将图像分类为不同的物体类别）。

假设我们有一个房价数据集，每个数据点包含房屋的特征（如面积、房间数、位置等）和对应的房价。通过监督学习算法，我们可以训练一个回归模型，根据房屋特征来预测房价。

假设有一个病人检测肿瘤数据集，通过监督学习算法，可以训练一个分类器，根据肿瘤大小和病人年龄来预测肿瘤为良性或恶性。

2. 无监督学习（Unsupervised Learning）

无监督学习（Unsupervised Learning）是机器学习的一种类型，它在没有标签的数据集上进行训练，即数据集中没有明确的输入和输出对。无监督学习的主要目标是从数据中发现隐藏的模式或结构，而不需要人工标注的数据。

无监督学习的主要类型

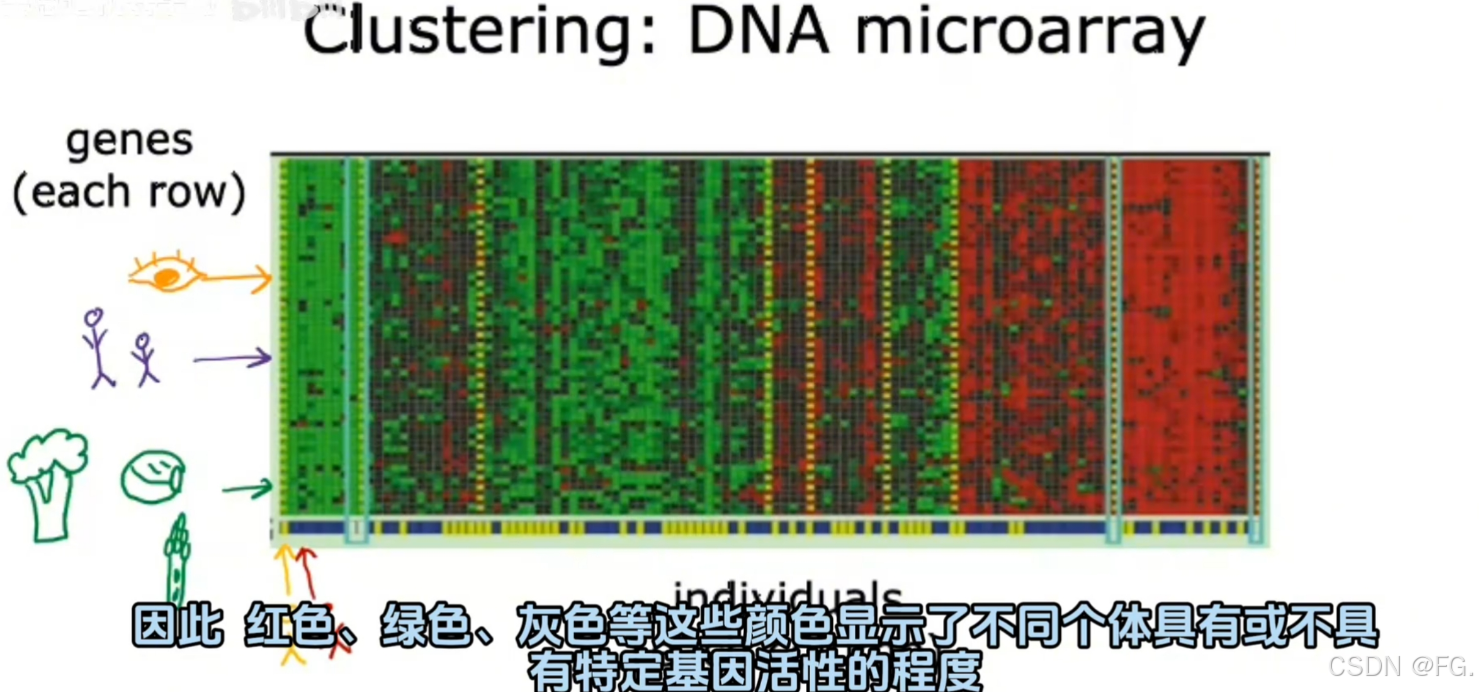
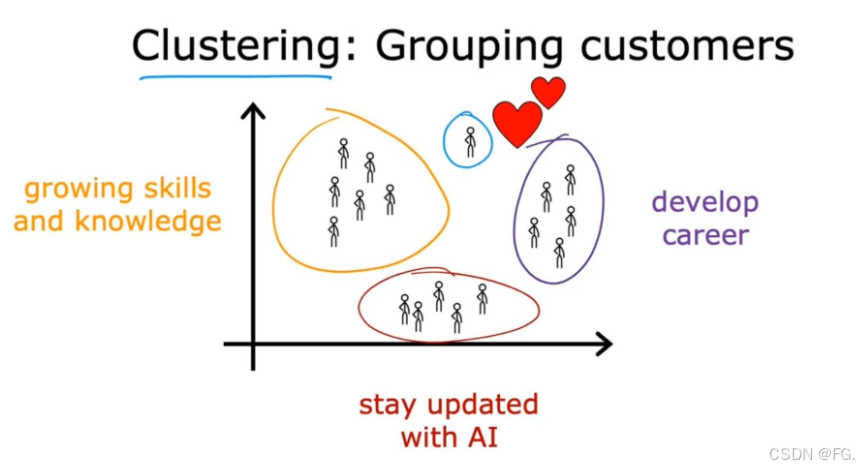
• 聚类（Clustering）：获取没有标签的数据并尝试自动将它们分组到集群中。

3. 线性回归模型（Linear Regression Model）

线性回归（Linear Regression）是一种用于预测连续数值的监督学习算法，它通过建立输入特征与输出变量之间的线性关系来预测输出。

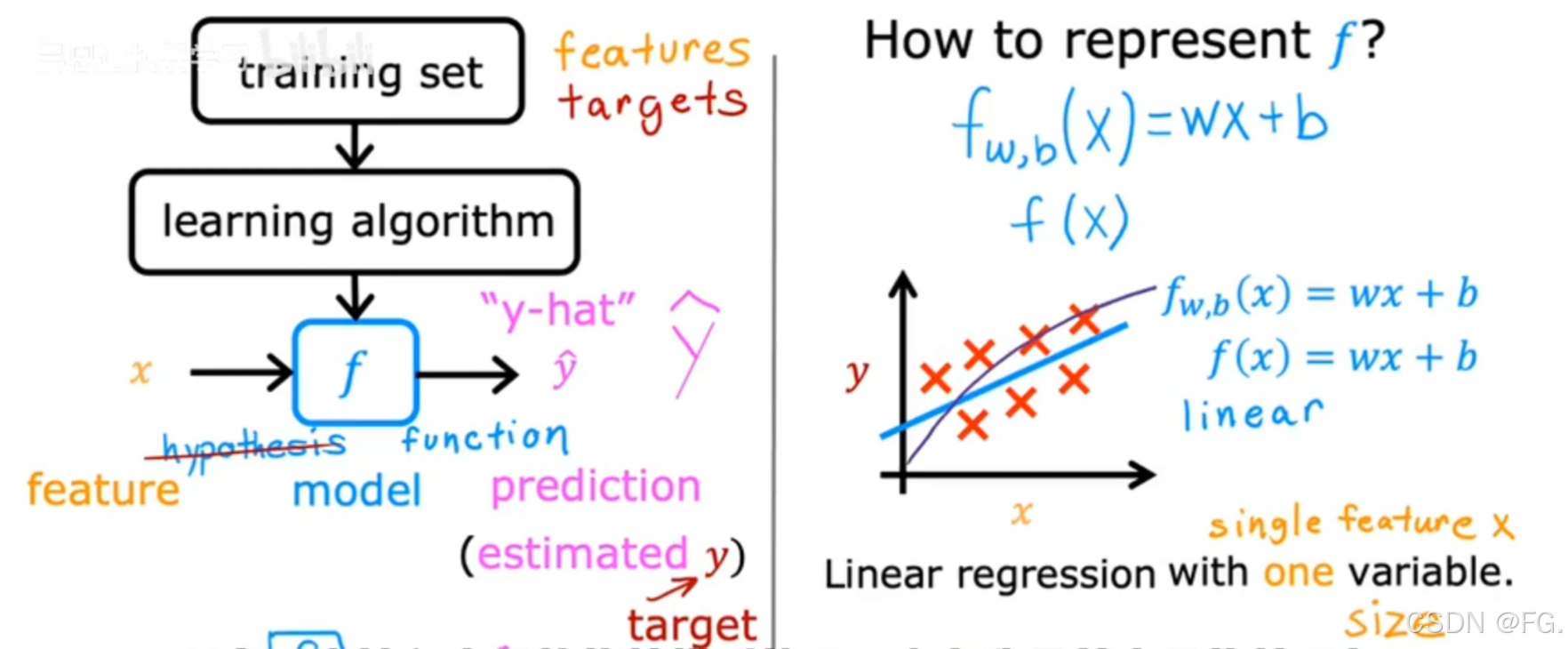
输入的训练集（输入特征。输出目标）通过学习算法构造函数 f，再将特征x输入学好的模型，输出预测结果 y-hat，直到结果接近真实目标值y。

4. 损失函数（Loss Function）

在机器学习中，代价函数（也称为损失函数）用于评估模型的预测结果与实际结果之间的差异。在线性回归中，常用的代价函数是均方误差（Mean Squared Error, MSE）。代价函数越小，说明模型的预测结果越接近实际值，因此训练模型的目标是最小化代价函数。

对于线性回归损失函数，要选择参数 w 和 b 的值，以便从函数 f 获得的直线以某种方式很好地拟合数据。

J(w, b)为损失函数

m是训练样本数量

f((x)(i))为第 i 个样本的预测值

y(i)是第 i 个样本的实际值

5. 梯度下降（Gradient Descent）

梯度下降是一种用于优化损失函数的迭代算法，通过逐步调整模型参数，使损失函数达到最小值。

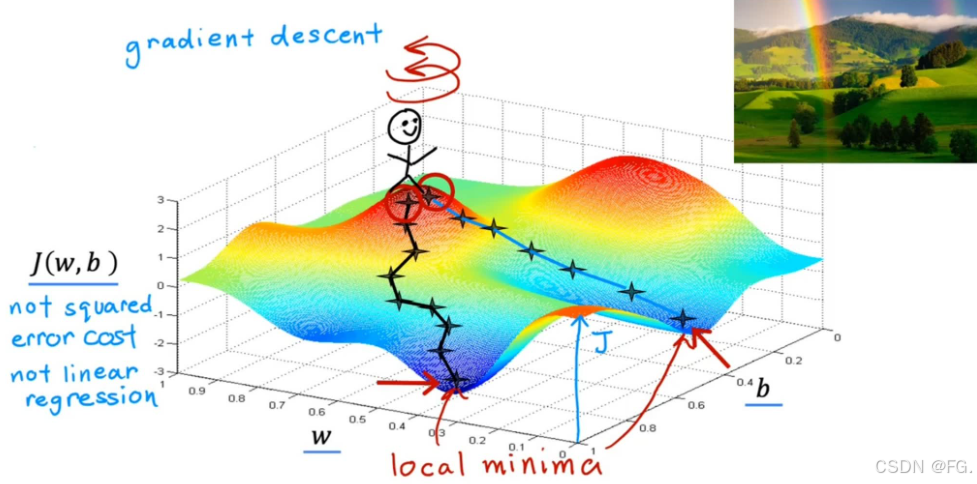
w，b 是模型参数。

α 是学习率，控制每次更新的步长。

偏导数：

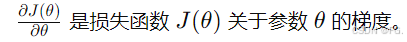
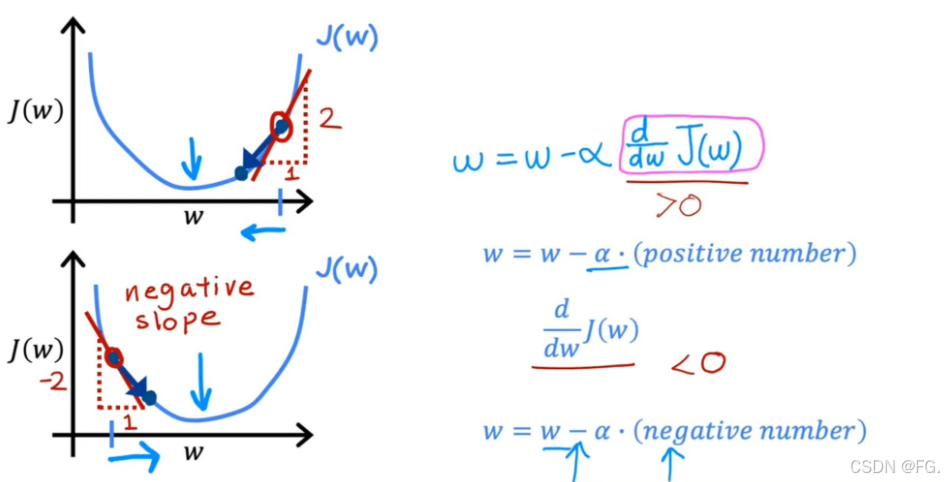
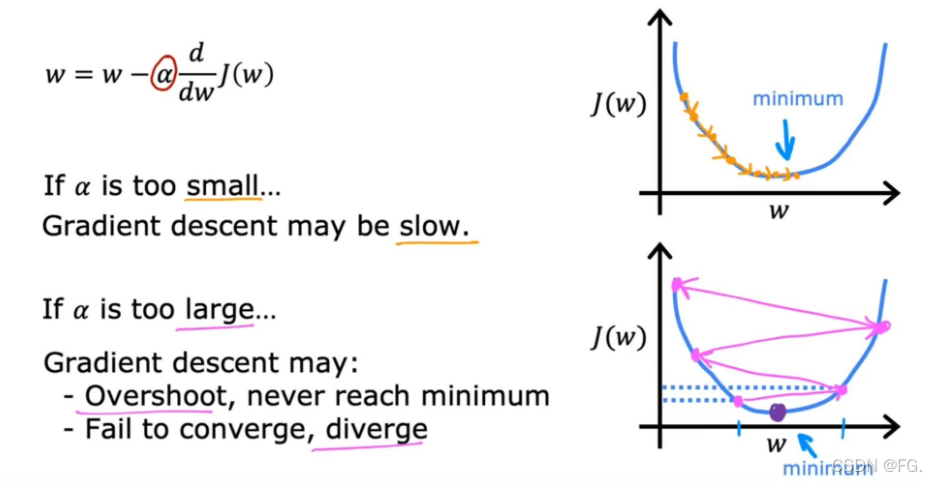
学习率 ：α 是梯度下降中一个重要的超参数。学习率过大可能导致参数更新过快，跳过最优解；学习率过小可能导致收敛速度过慢。通常通过实验和调参来选择合适的学习率。

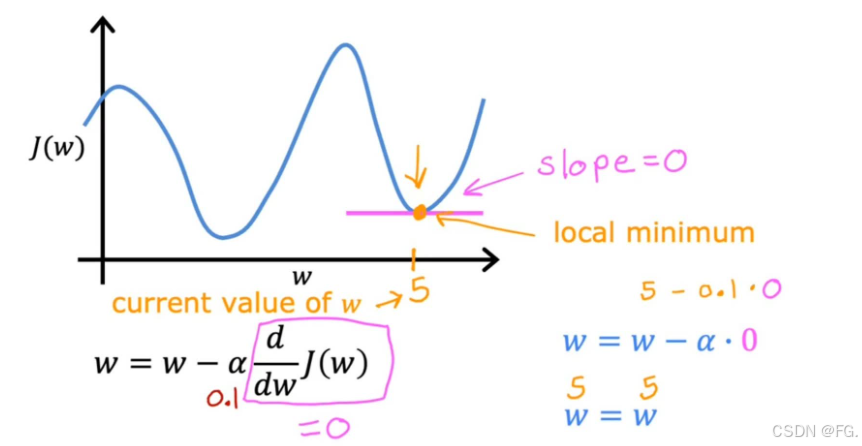
如果梯度下降接近局部最小值时，导数会自动变小，即使 α 保持在某个固定值。

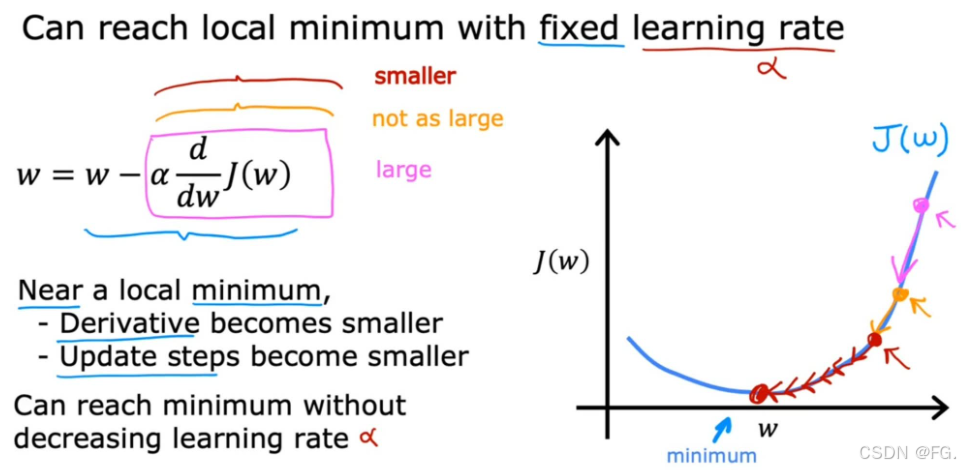
6. 线性回归梯度下降（Gradient Descent for Linear Regression）

参数更新规则：

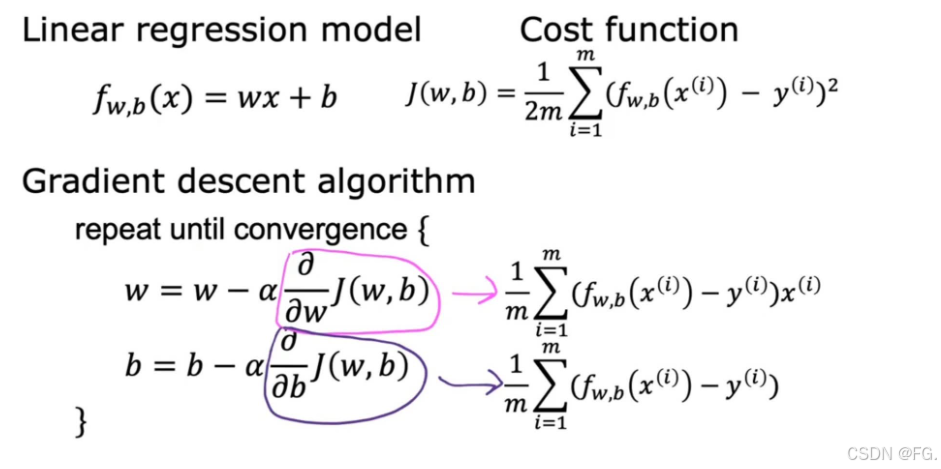
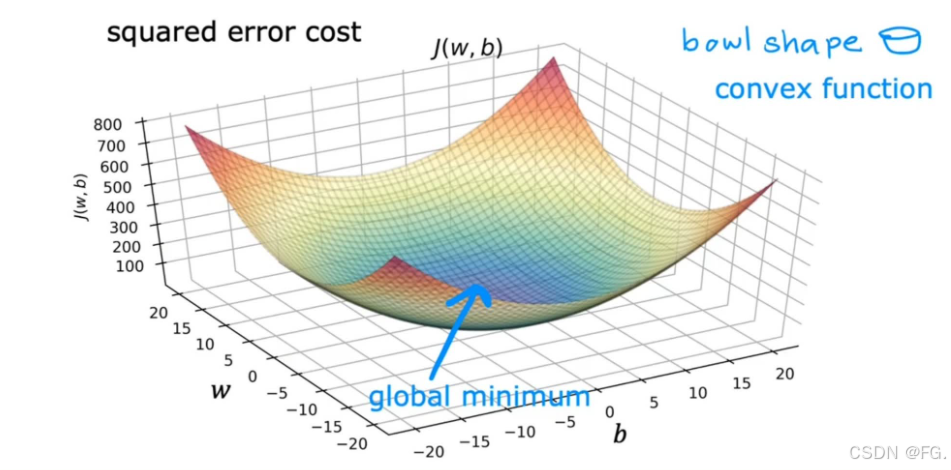
线性回归的损失函数（通常是均方误差，MSE）是一个凸函数，这意味着它只有一个全局最小值，而没有多个局部最小值。

不断运行梯度下降进行数据拟合，成本函数越靠近等高线图的中心圈，w，b越接近最优解。

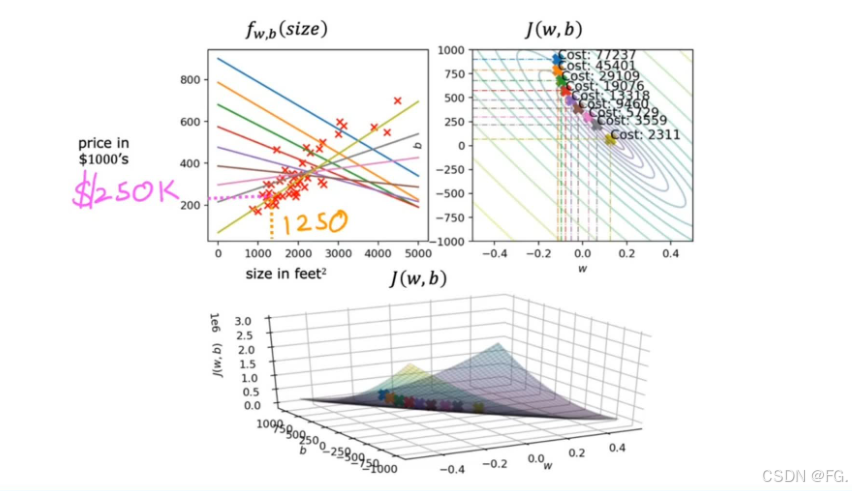
批量梯度下降（Batch Gradient Descent）用于最小化损失函数并找到最佳的模型参数。在批量梯度下降中，每次迭代使用整个训练集来计算梯度和更新参数。

7. 多类特征（Multiple features）

通过多个输入特征进行预测结果输出，通过结合多个特征，模型能够捕捉更复杂的关系和模式，从而提高预测的准确性。

将参数 w 和 特征 x 进行矢量化，通过向量的内积求得模型函数。

8. 向量化（Vectorization）

向量化是将数据转换为向量形式的过程。

下图对比了向量化前和后的求模型函数的方法：

d 为导数，这里表示 w 的变化量，通过减去变化量不断更新 w 的值。

9. 多元线性回归的梯度下降法（Gradient Descent for Multiple Regression）

函数执行梯度下降迭代，更新参数并记录每次迭代的损失。

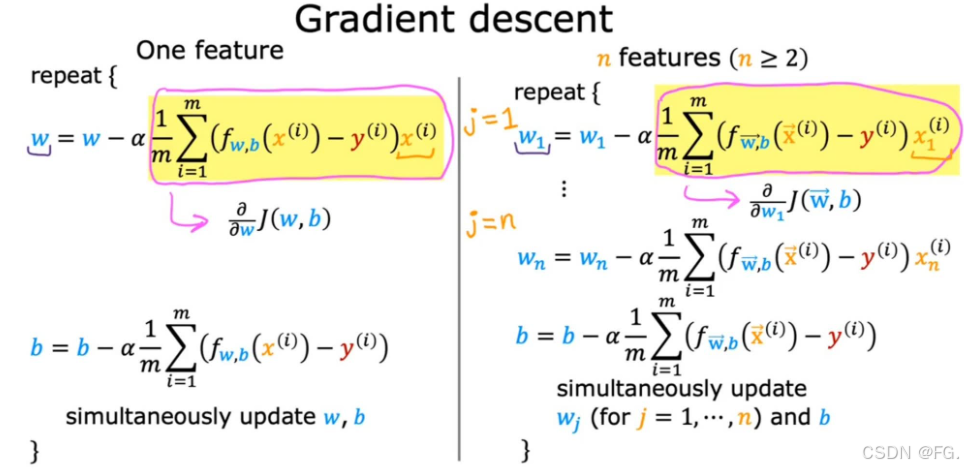
10. 特征缩放（Feature scaling）

特征缩放是数据预处理的重要步骤，旨在将不同特征的值缩放到一个相似的范围，以提高机器学习模型的性能和训练速度。

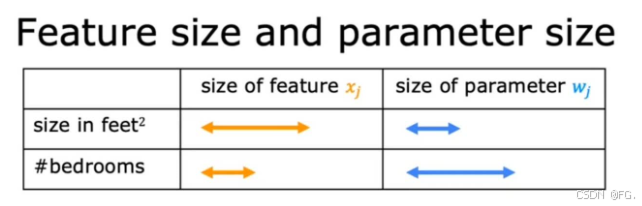
当一个特征的值范围大时，对应的参数范围有必要小；反之。

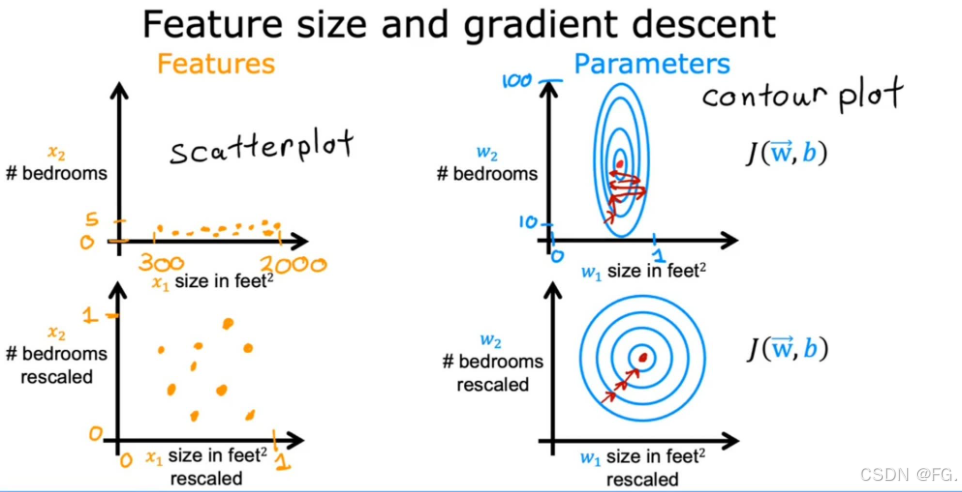
当有不同的功能，具有非常不同的值范围时，它会导致梯度下降运行缓慢；但重新缩放不同的功能，它们的值具有可比的值范围后就可以显著加快梯度下降。

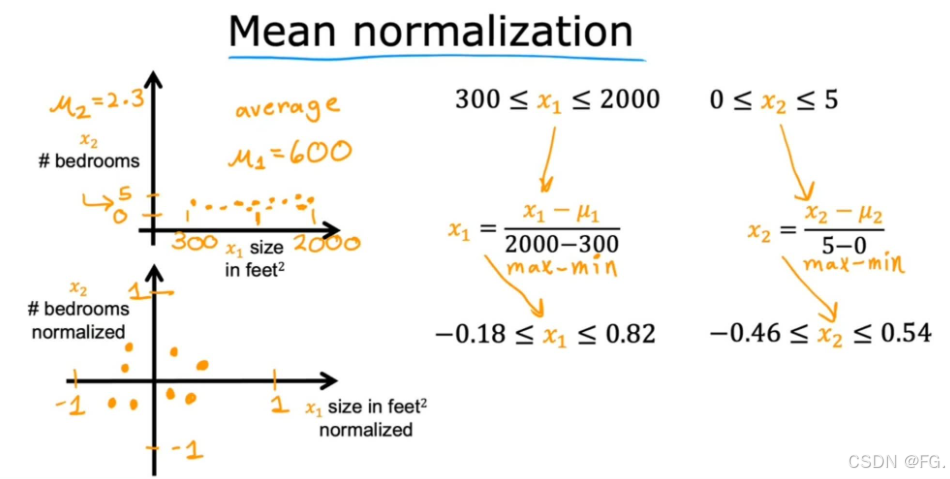
• 标准化（Standardization）（也称为Z-score normalization） ：将特征缩放到均值为0、标准差为1的分布。适用于大多数机器学习算法。
  
  

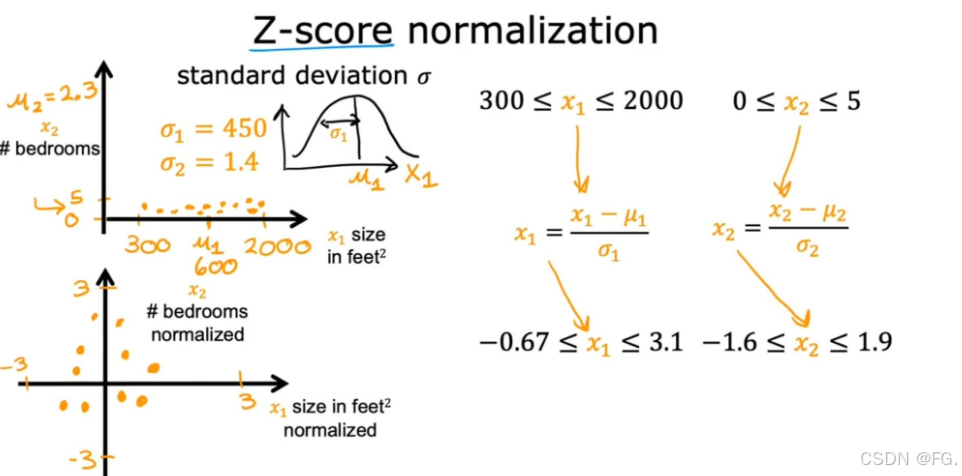
• 最大绝对值缩放（MaxAbsScaler） ：将每个特征的值缩放到[-1, 1]之间，适用于数据已经中心化为0且包含负值的情况。
  

  

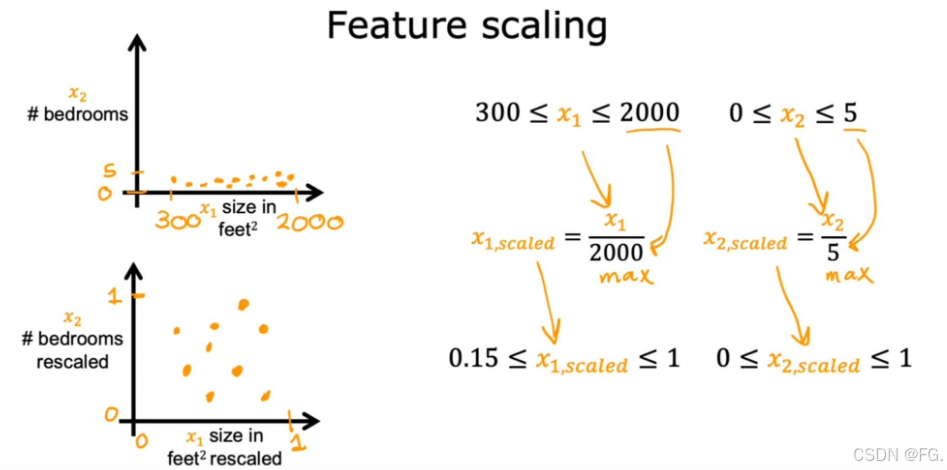
• 归一化（Normalization） ：将特征缩放到特定范围（通常是0到1）。适用于需要特征具有相同量纲的算法，如神经网络和基于距离的算法。
  

11. 检查梯度下降是否收敛（Checking Gradient Descent for Convergence）

横轴为梯度下降的迭代次数，纵轴为成本值。

当曲线达到平稳时，梯度下降接近于收敛。

自动收敛测试：设置一个固定值 ε，如果成本值在一次迭代中小于 ε，则梯度下降收敛。

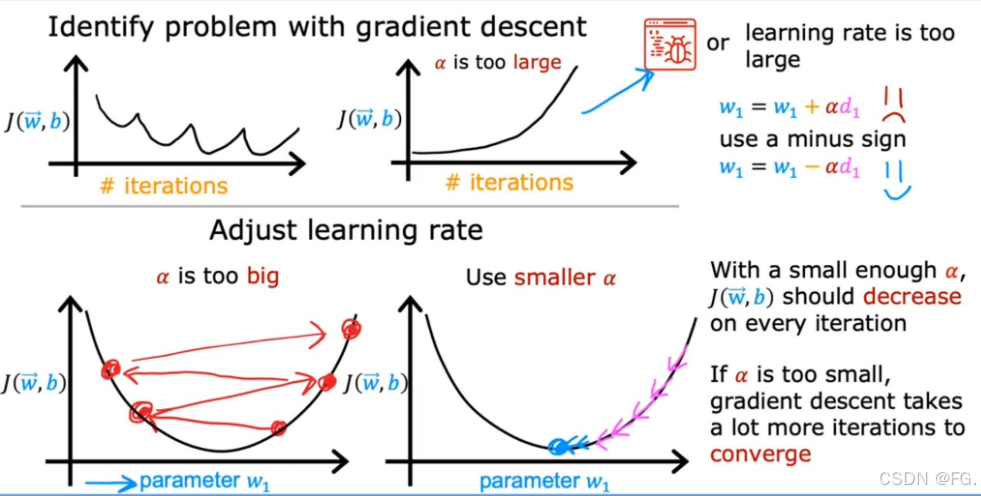
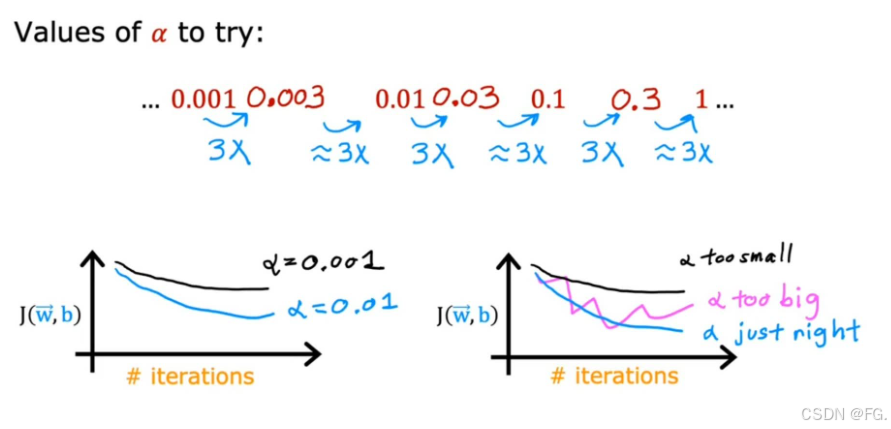
12. 学习率的选择（Choosing the Learning Rate）

如果 α 太小，梯度下降速度太慢；如果太大，梯度下降可能不会收敛。

13. 特征工程（Feature Engineering）

特征工程是指在机器学习和数据分析中，通过对原始数据进行特征提取、转换和选择，以创建能够更好地反映问题本质、提升模型性能的特征的过程。特征工程对于模型的最终性能有着重要的影响，它能够帮助模型更好地理解数据，提取有效的信息，从而提高模型的准确性和泛化能力。

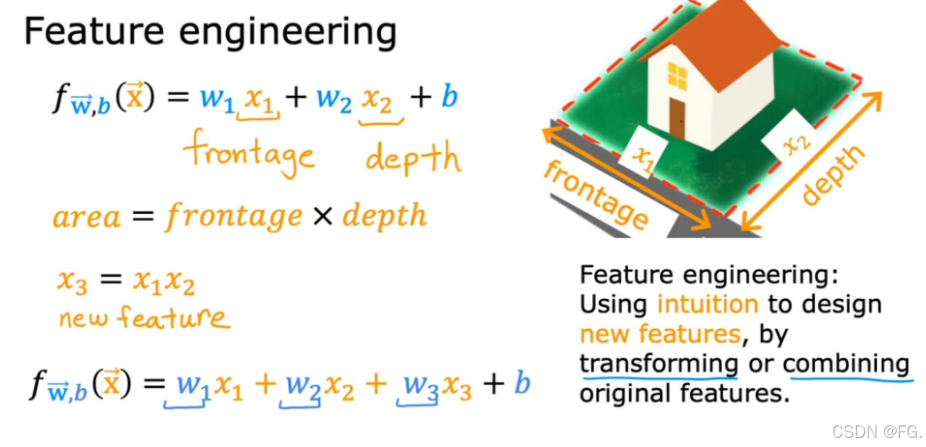
14. 多项式回归（Polynomial Regression）

多项式回归是线性回归的一种扩展形式，它通过增加特征的高次项来拟合数据中的非线性关系。与普通线性回归不同，多项式回归可以更灵活地适应数据的曲线形态，因此在处理非线性数据时特别有效。

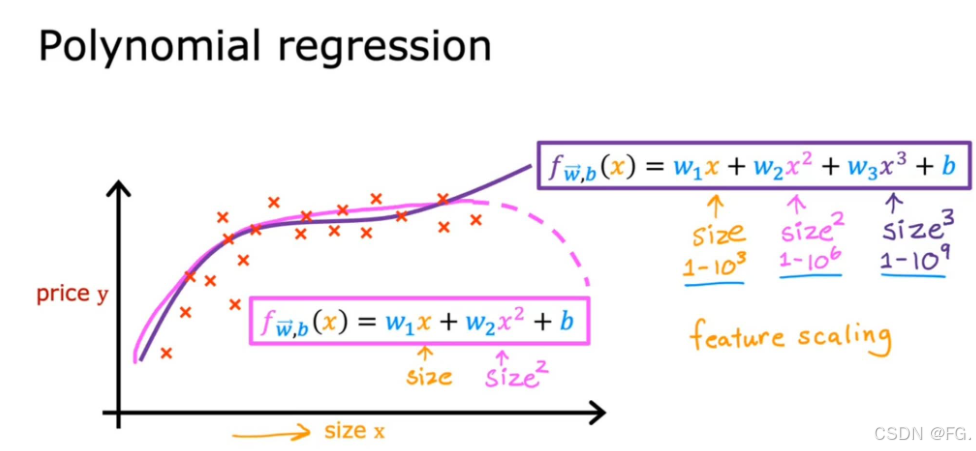
15. 逻辑回归（Logistic Regression）

逻辑回归是一种广泛使用的分类算法，主要用于解决二分类问题。尽管名称中带有"回归"，但逻辑回归实际上是一种分类算法，因为它预测的是离散的类别标签。

16. 决策边界（Decision Boundary）

逻辑回归的决策边界是由线性方程 z=0 确定的。

令 w1 = w2 = 1，b = -3，令 z = 0，则

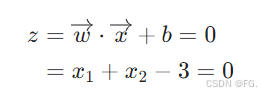
画出 x1 与 x2 的直线图，即为决策边界。

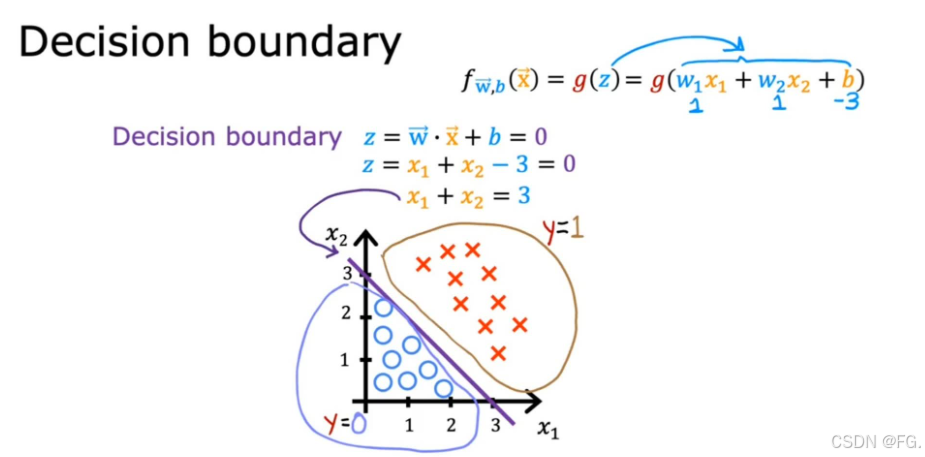
令 w1 = w2 = 1，b = -1，则

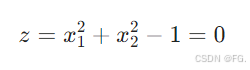
画出图像为一个单位圆，这个单位圆即为决策边界。

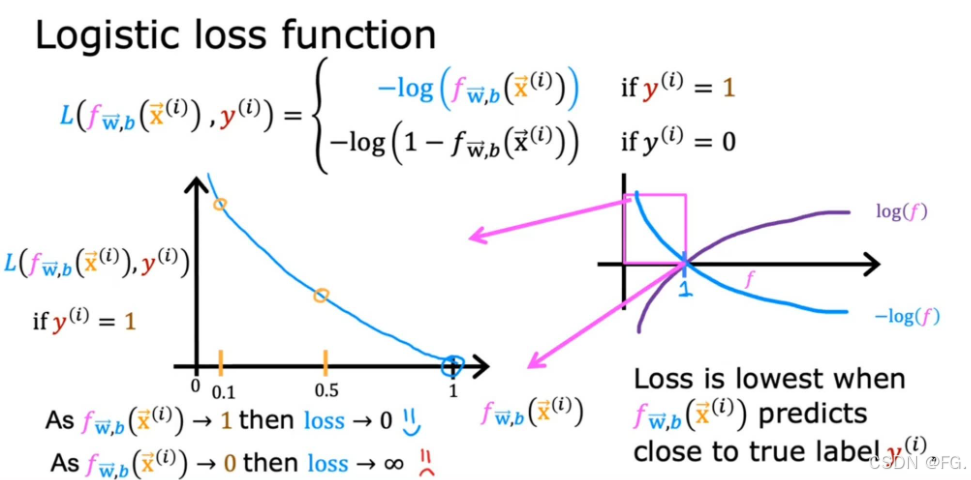
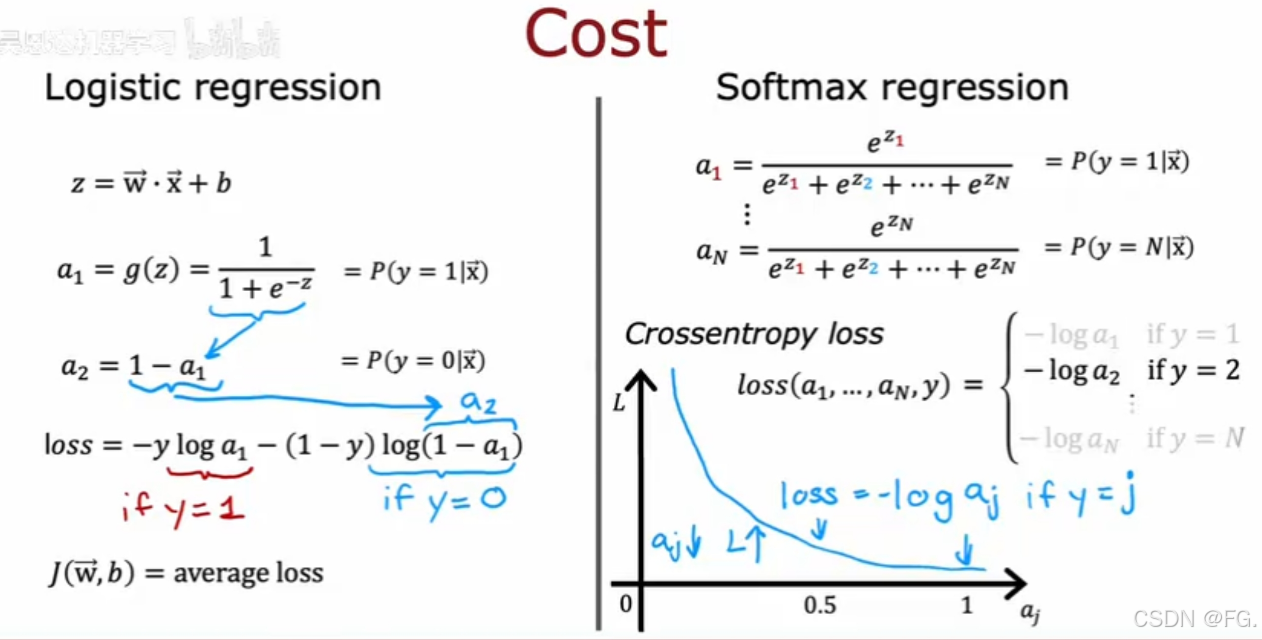
17. 逻辑回归的代价函数（Cost Function for Logistic Regression）

在逻辑回归中，代价函数（也称为损失函数）用于衡量模型预测与实际结果之间的差距，并指导模型参数的优化。对于逻辑回归，代价函数是基于似然函数的对数表示，即对数似然函数。最大化对数似然函数等价于最小化负对数似然函数，后者通常被用作代价函数。

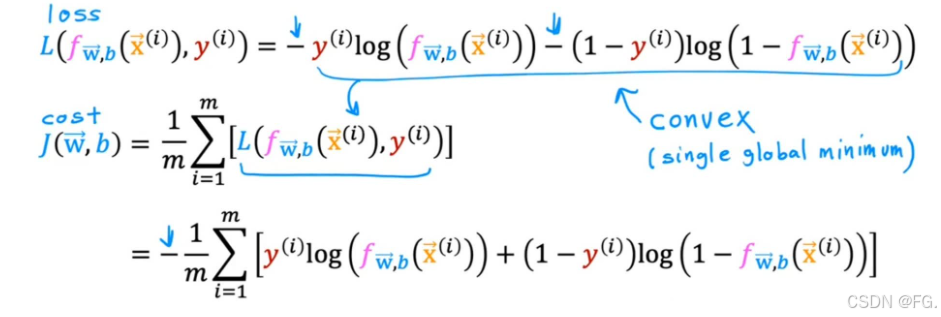
18. 梯度下降实现（Gradient Descent Implement）

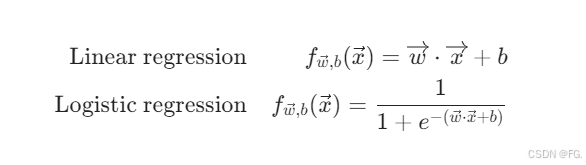
19. 过拟合（Overfitting）与欠拟合（Underfitting）

在机器学习中，过拟合（Overfitting）是指模型在训练数据上表现非常好，但在未见过的测试数据或新数据上表现较差的一种现象。过拟合意味着模型在训练数据中学习到了过多的噪声和细节，而不是学习到了数据的通用特征。这样一来，模型的泛化能力变差，在实际应用中效果不佳。

欠拟合是指模型过于简单，无法捕捉数据的内在规律，导致在训练数据和测试数据上的表现都很差。欠拟合通常发生在模型的复杂度太低的情况下，例如使用线性模型来拟合非线性数据。

过拟合是指模型过于复杂，捕捉到了训练数据中的噪声和细节，虽然在训练数据上的表现非常好，但在测试数据上的表现很差。过拟合通常发生在模型的复杂度太高的情况下，例如使用高次多项式来拟合数据。

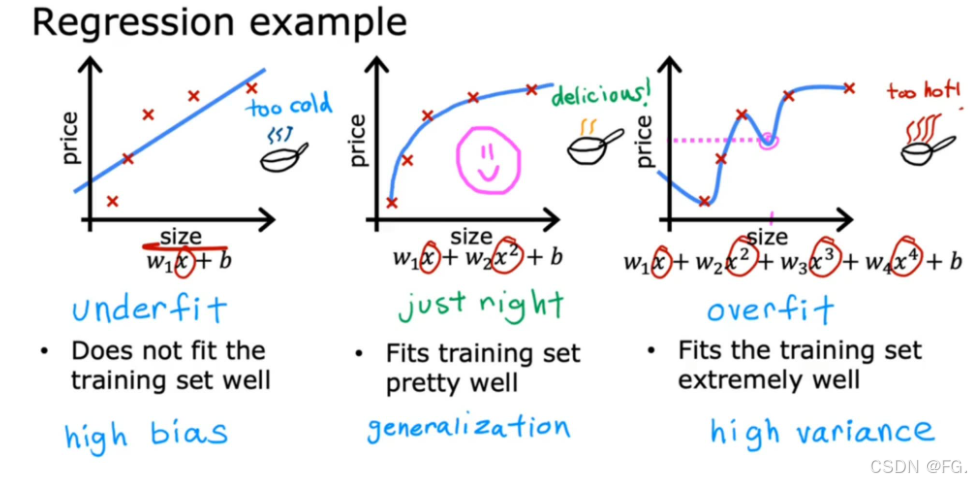
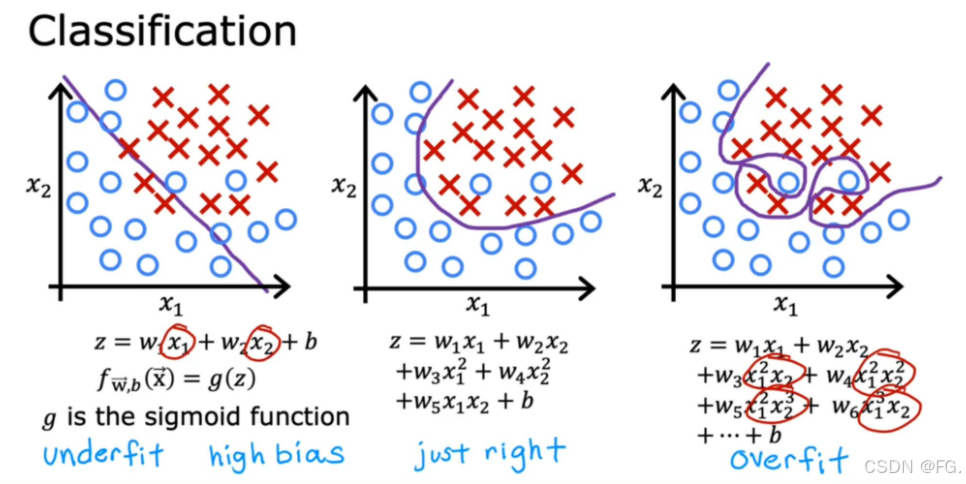
20. 解决过拟合的方法（Addressing Overfitting）

• 增加训练数据：更多的数据可以帮助模型更好地捕捉数据的总体分布，减少过拟合的可能性。

• 简化模型：减少模型的复杂度，例如减少参数数量，使用更简单的模型（如决策树的最大深度，神经网络的层数和每层的神经元数等）。

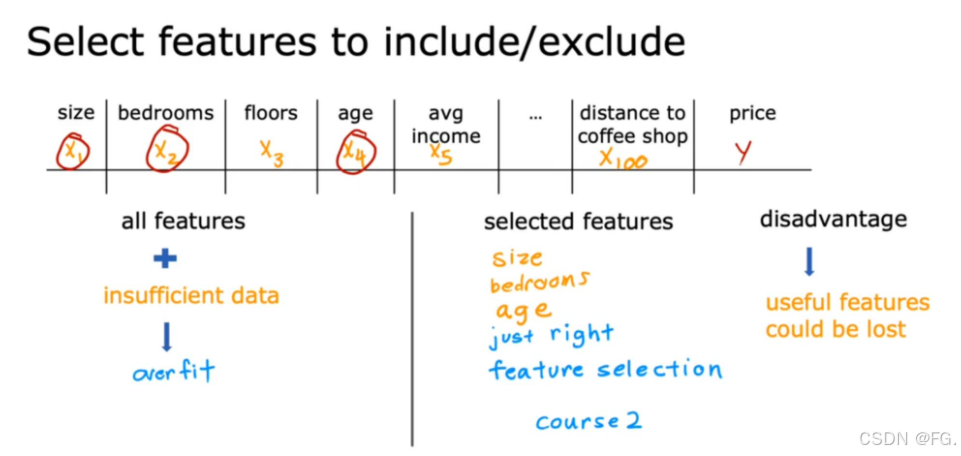
• 正则化：在损失函数中加入正则化项，可以限制模型参数的大小，防止模型过于复杂。常见的正则化方法包括L1正则化（Lasso）和L2正则化（Ridge）。

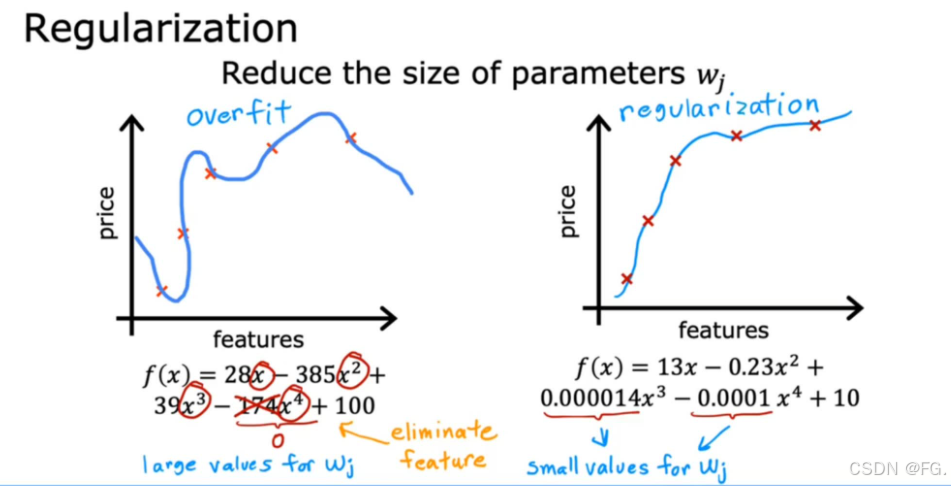
21. 正则化代价函数（Cost Function with Regularization）

正则化是机器学习中防止过拟合的一种技术。它通过在模型的损失函数中增加一个正则化项来限制模型的复杂度，从而提高模型在新数据上的泛化能力。

• L1正则化：L1正则化在损失函数中增加一个正则化项，使得新的损失函数为：
  

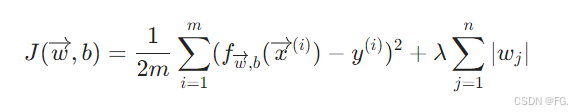
  其中 𝜆 是正则化强度的超参数，|wj|是参数 wj 的绝对值。

• L2正则化：L2正则化在损失函数中增加一个正则化项，使得新的损失函数为：
  

  其中 𝜆 是正则化强度的超参数，wj²是参数 wj 的平方。

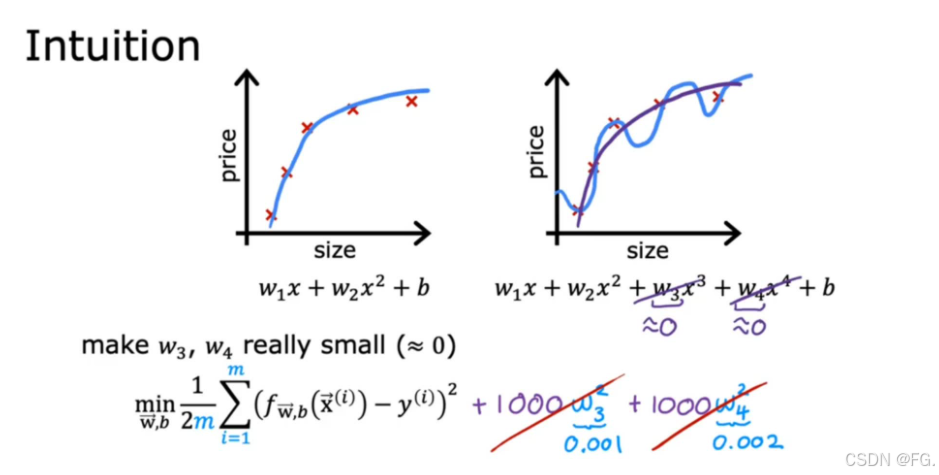
22. 正则化线性回归（Regularized linear regression）

正则化线性回归是指在标准线性回归模型中加入正则化项，通过惩罚过大的参数来防止过拟合，提高模型的泛化能力。

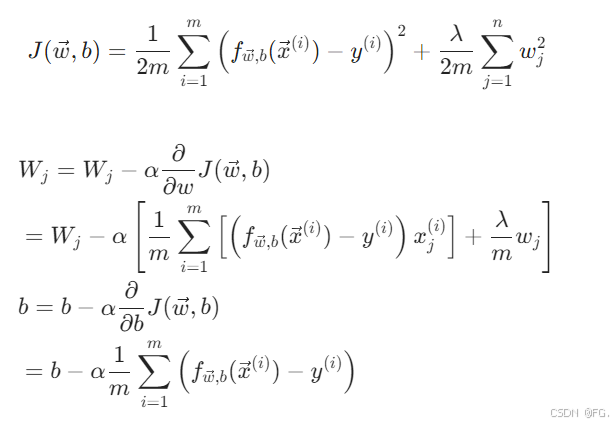
23. 正则化逻辑回归（Regularized Logistic regression）

计算过程就省略了。。。

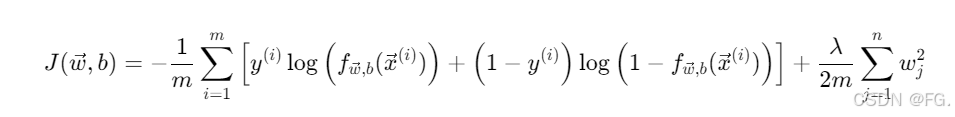
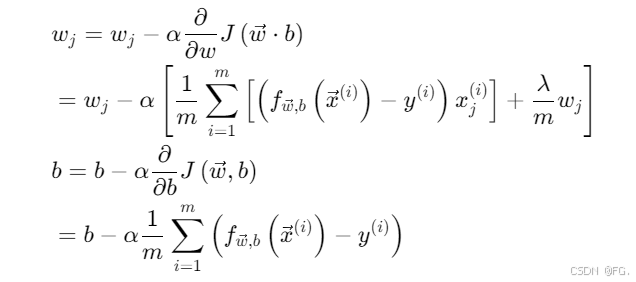
24. 构建一个神经网络（Building a neural network）

• Dense 层，也称为全连接层或密集层，实现的是对输入进行线性变换并应用激活函数。它是最常见的层类型，尤其是在多层感知器（MLP）模型中。
• sequential函数用于顺序构建一个神经网络模型。它将多个子模块（层）按顺序放置，每个子模块会依次将前一层的输出作为输入进行计算。
• model.compile()是 Keras 库中用于配置模型训练的函数，在使用 Keras 搭建神经网络模型后，需调用 model.compile 来指定优化器、损失函数以及评价指标，才能进行训练。

model.compile(optimizer, loss, metrics=None, loss_weights=None, sample_weight_mode=None, weighted_metrics=None, target_tensors=None, distribute=None, **kwargs)

optimizer: 指定优化器，常用的有 'sgd'（随机梯度下降）、'adam'、'rmsprop' 等，或者使用 Keras 提供的优化器类，如 tf.keras.optimizers.SGD。

loss: 指定损失函数，用于计算模型的损失值，常用的有 'mse'（均方误差）、'binary_crossentropy'（二元交叉熵）、'categorical_crossentropy'（分类交叉熵）等。

metrics: 指定评估指标，常用的有 'accuracy'、'mae'（平均绝对误差）等，可以是字符串列表，也可以是自定义的函数。

loss_weights: 可选，列表或字典，指定损失函数的权重。

sample_weight_mode: 可选，'temporal' 或 None，用于处理时间序列数据。

weighted_metrics: 可选，列表，指定用于加权的评估指标。

target_tensors: 可选，TensorFlow 张量，作为目标数据的张量。

distribute: 可选，用于分布式训练。

kwargs: 其他参数。

• model.fit()是 Keras 中用于训练模型的函数，它执行给定数量的训练迭代（epochs），并将训练数据按批次（batches）送入模型进行训练。

model.fit(x, y, batch_size=None, epochs=1, verbose=1, callbacks=None,      validation_split=0.0, validation_data=None, shuffle=True, class_weight=None, sample_weight=None, initial_epoch=0, steps_per_epoch=None, validation_steps=None, validation_batch_size=None, validation_freq=1, max_queue_size=10, workers=1, use_multiprocessing=False)

x: 输入数据，可以是 NumPy 数组、TensorFlow 张量、Pandas 数据框或 tf.data 数据集。

y: 目标（标签）数据，与 x 对应。

batch_size: 每次梯度更新的样本数。如果未指定，默认为 32。

epochs: 训练的轮数。每轮训练是对整个输入数据的遍历。

verbose: 日志显示模式。0 = 不显示日志信息，1 = 显示进度条，2 = 每轮显示一行。

callbacks: 回调函数列表，在训练过程中的特定点被调用。

validation_split: 在 0 和 1 之间浮动的小数，用来指定训练数据的一部分作为验证集。

validation_data: 验证数据，元组 (x_val, y_val) 或 (x_val, y_val, val_sample_weights)。

shuffle: 是否在每轮迭代前混洗数据。

class_weight: 字典，用于指定不同类的权重。

sample_weight: 用于权重训练样本的 NumPy 数组。

initial_epoch: 从该轮开始训练。

steps_per_epoch: 每轮训练的步数（批次数）。

validation_steps: 每次验证的步数。

validation_batch_size: 验证数据的批次大小。

validation_freq: 验证模型的频率。

max_queue_size: 生成器队列的最大容量。

workers: 用于数据加载的工作线程数。

use_multiprocessing: 是否使用多进程数据加载。

25. 在一个单层中的前向传播（Forward prop）

前向传播（Forward Propagation）是神经网络中计算输入数据经过网络得到输出结果的过程。在前向传播过程中，输入数据通过网络中的各层逐层传递，每层执行相应的计算，最终得到网络的输出。

26. 神经网络如何高效实现（How neural networks are implemented efficiently）

matmul函数用于执行矩阵乘法，与 np.dot 类似，但在处理高维数组时更灵活。

27. 训练细节（Training Details）

28. 激活函数（Activation Functions）

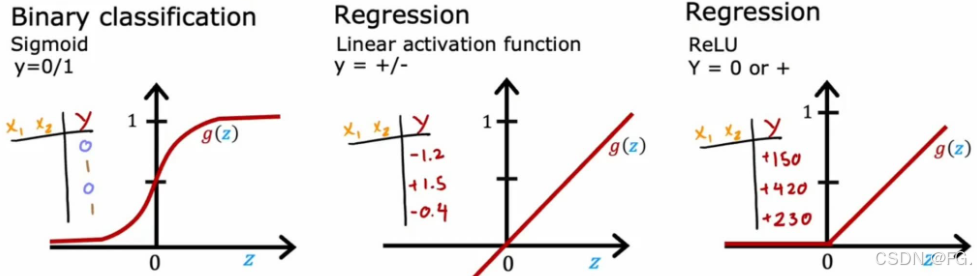
29. Softmax函数

Softmax函数是一种常用于多分类问题的激活函数，特别是在神经网络的输出层。它将一组未归一化的数值（即原始的分类得分）转换为概率分布。

在多分类神经网络中，Softmax函数通常用于输出层，以生成每个类的预测概率。例如，在图像分类任务中，模型可能有多个输出节点，每个节点对应一个类，Softmax函数将这些节点的输出转换为概率分布。

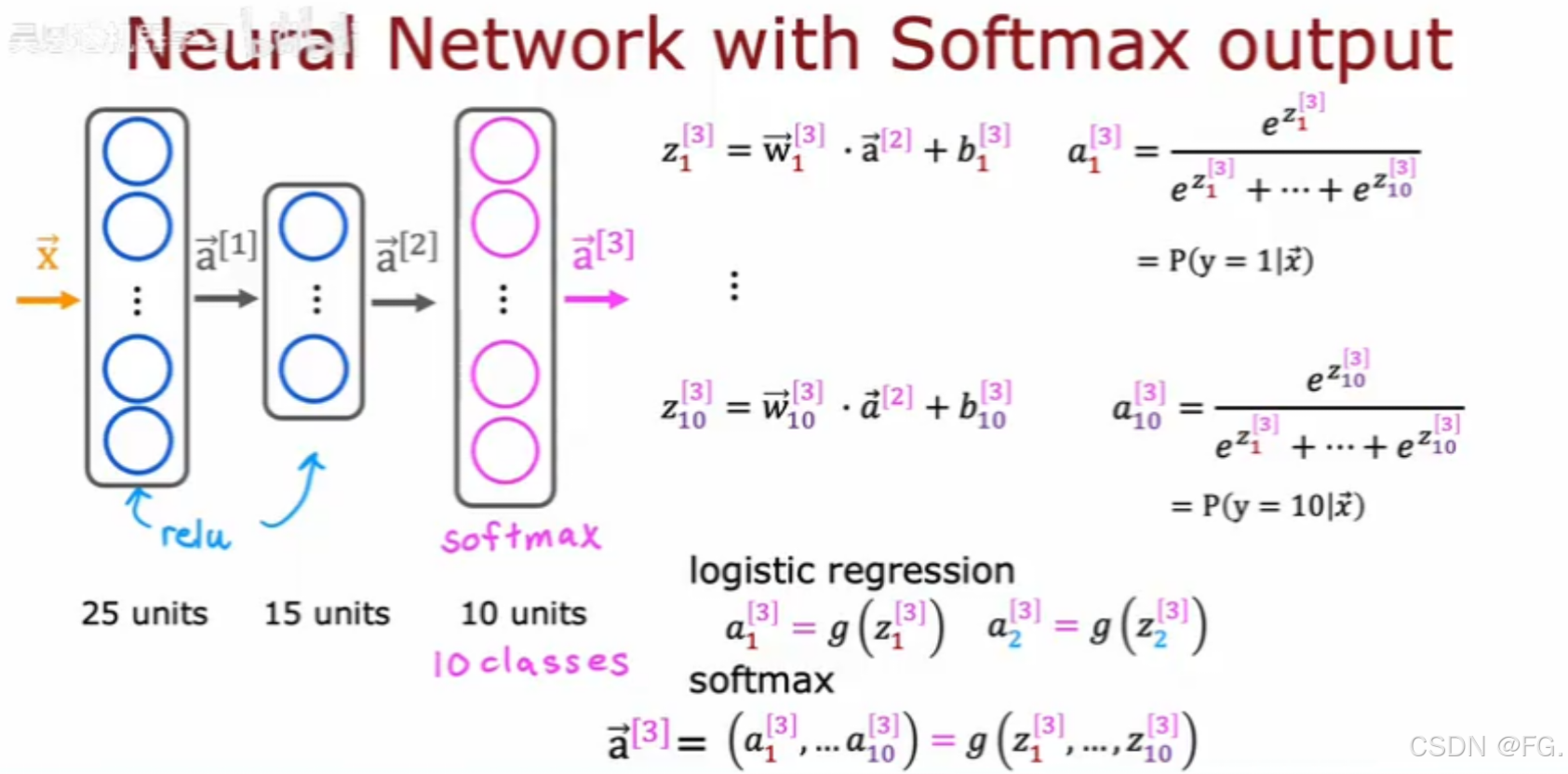
softmax的改进实现

30. 多个输出的分类（Classification with multiple outputs）

多标签的分类可以通过构建一个神经网络同时进行识别。

31. 模型评估（Evaluating model）

• 误差成本平方的回归（Train/test procedure for linear regression）：即使训练例子的平均误差将为0或非常接近0，但如果在测试集中有一些额外的例子是算法没有训练过的，即训练集实际上不太擅长推广到新的示例，那么测试用例预测的结果就会有很大差距。

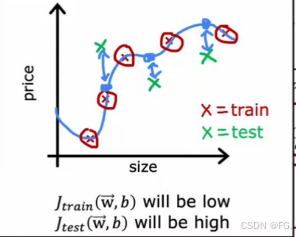
• 分类问题（Train/test procedure for classification problem）：通过模型在训练集和测试集上分类错误的分数来看模型的性能。

32. 模型选择和训练交叉验证测试集（Model selection and training/cross validation/test sets）

将数据分为三部分，分别为训练集、交叉验证集、测试集。

交叉验证集（额外数据集）用来检查或交叉检查有效性或者不同模型的准确性。

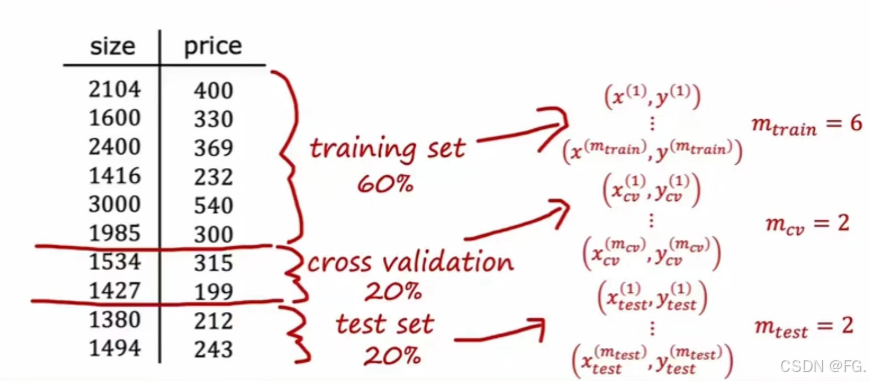
先通过训练集和交叉测试集来评估模型，然后通过测试集再一次评估模型，这样确保不会意外地将任何东西适合到测试集中，因此对于测试集是一个公平的算法泛化误差的估计。

33.诊断偏差和方差（Diagnosing bias and variance）

偏差（Bias）指的是模型预测值与真实值之间的系统性误差。偏差高通常意味着模型过于简单，无法捕捉数据中的复杂模式，导致欠拟合。

• 高偏差：模型对训练数据和测试数据都表现不佳，误差较大。模型过于简单，不能很好地拟合数据。
• 低偏差：模型能很好地拟合训练数据。

方差（Variance）指的是模型预测值的波动性，即模型对训练数据的变化是否敏感。方差高通常意味着模型过于复杂，过度拟合训练数据，但在测试数据上表现不佳。

• 高方差：模型在训练数据上表现良好，但在测试数据上表现较差。模型过于复杂，过拟合了训练数据。
• 低方差：模型对训练数据和测试数据都有稳定的表现。

线性回归：偏差高，因为它无法捕捉数据中的非线性关系。训练误差和测试误差都较高。

多项式回归（10阶）：方差高，因为它过度拟合了训练数据。训练误差较低，但测试误差较高。

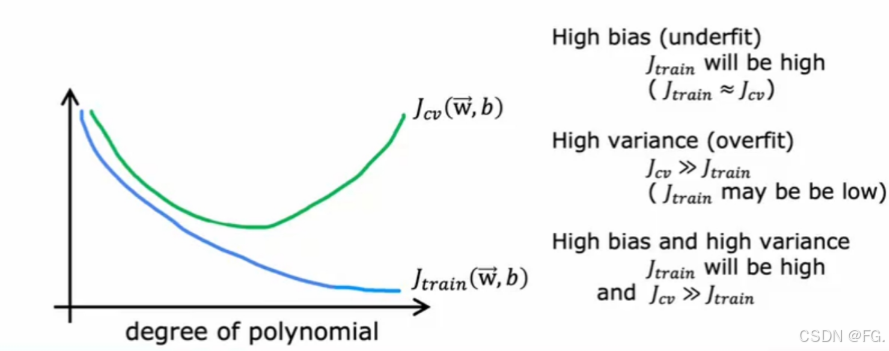
如果你的学习算法有很高的偏差或不适合数据，关键指标是训练集的成本函数是否高；如果有高方差，关键指标是交叉测试集的成本比训练集的大得多；如果同时具有高偏差和高方差，关键指标是训练集成本函数高且交叉测试集成本远大于训练集的成本。

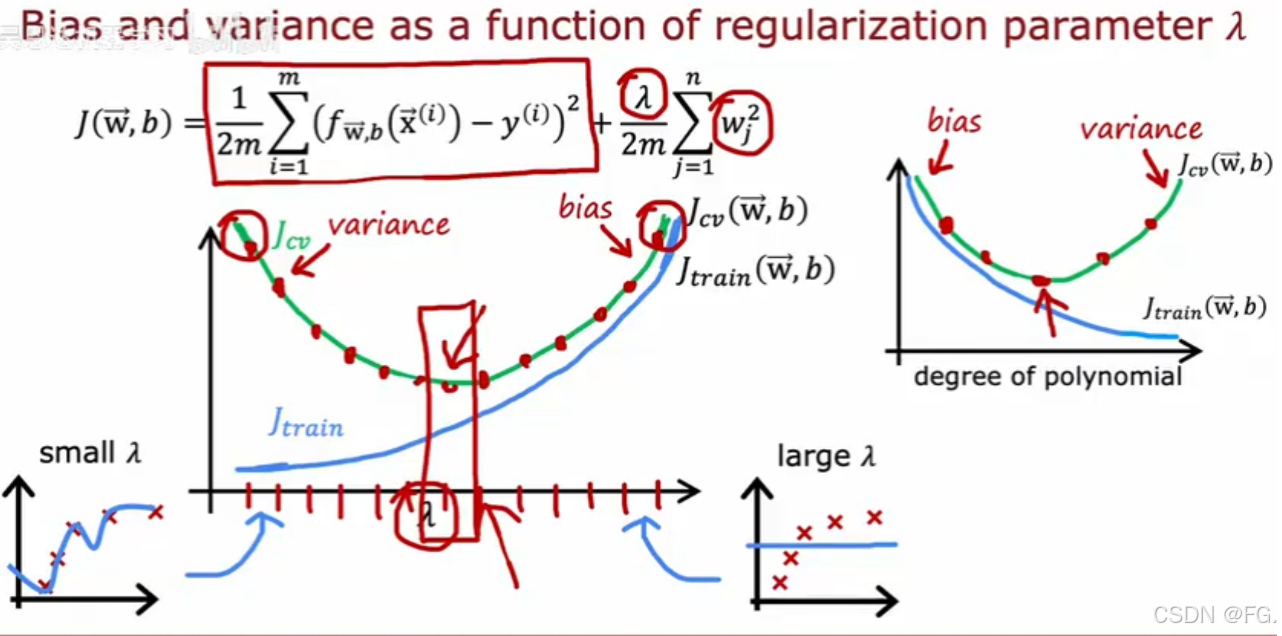
34. 正则化和偏差或方差（Regularization and bias/variance）

• 正则化参数过小：模型权重（系数）受到的约束很小，允许模型变得非常复杂，容易过拟合训练数据。
• 正则化参数过大：模型权重（系数）受到的约束很大，模型被迫简单化，无法有效捕捉数据中的复杂关系。

35. 建立表现基准（Establishing a baseline level of performance）

建立基准性能水平的常见方法：

• 当你使用非结构化数据时，人类级别的性能通常是一个很好的基准。
• 使用竞争性算法建立一个基准。
  

36.学习曲线（Learning curves）

学习曲线是评估机器学习模型性能的工具，通过展示模型在训练集和验证集上的错误率或准确率随训练样本数量变化的情况，可以帮助我们诊断模型是否存在过拟合或欠拟合问题。学习曲线通常显示训练误差和验证误差随训练样本数量增加的变化情况。

测试集的错误通常比训练集的高，因为参数都拟合到了训练集。

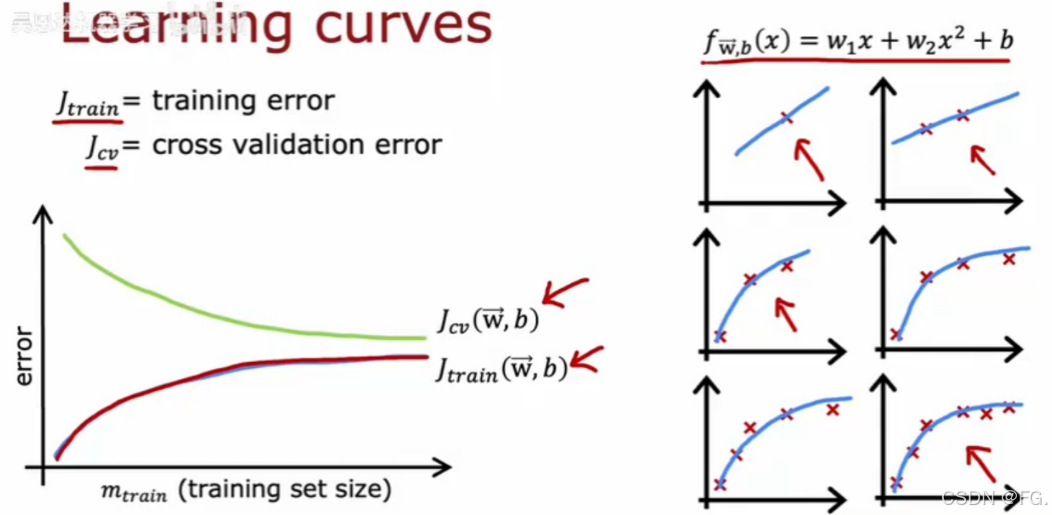
对于高方差（欠拟合），训练误差和验证误差都很高，且随训练样本数量增加变化不大，过多的训练集对模型优化起不到太大作用。

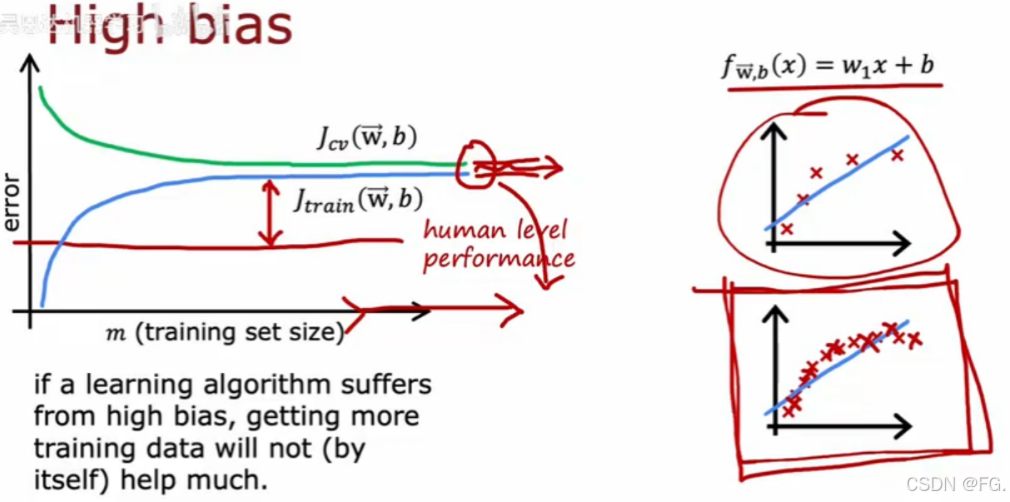
对于高方差（过拟合），训练误差很低，但验证误差很高，两者之间有明显差距，可增加训练集来优化模型。

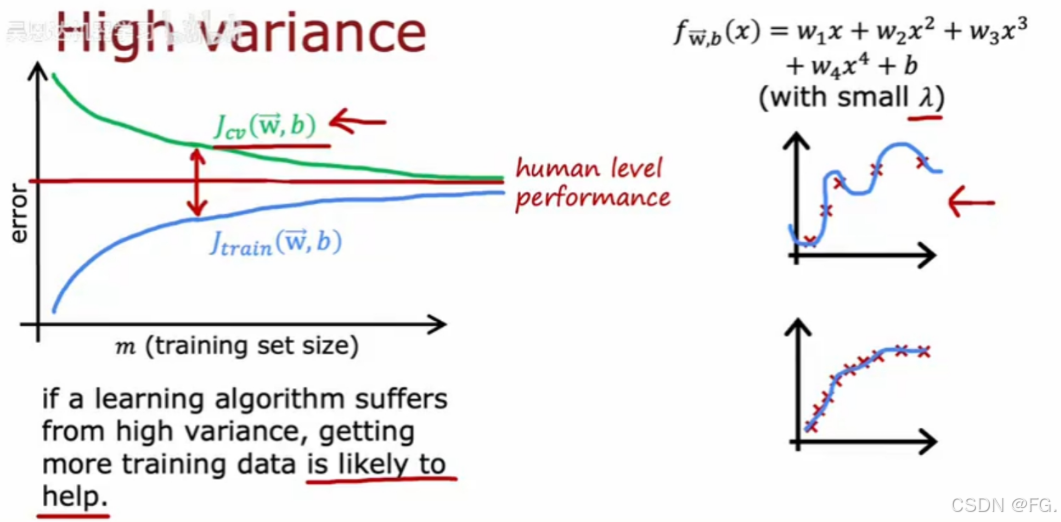
37. 偏差或方差与神经网络（Bias/variance and neural networks）

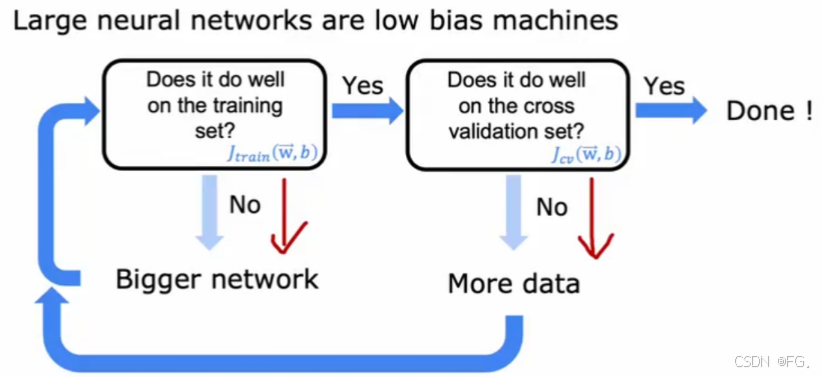
小型神经网络转为大型，如果适当地规则化更大的神经网络，效果可能会更好，但会减缓训练和推理过程导致成本增加。

38. 误差分析（Error analysis）

误差分析是机器学习模型评估和改进过程中的一个重要环节。通过对模型的误差进行深入分析，我们可以了解模型表现不佳的原因，并采取相应的措施进行改进。误差通常分为以下几类：

• 偏差（Bias）：反映了模型对训练数据的拟合能力。高偏差表示模型欠拟合。
• 方差（Variance）：反映了模型对训练数据的敏感程度。高方差表示模型过拟合。
• 噪声（Noise）：数据中的不可避免的随机误差。

假设500例交叉测试集，其中有100例算法分类出了错误，需要手动地去检验和分类；假如数量庞大，需从中抽取一部分样本出来进行最常见的错误类型的足够统计数据，进而更好地去分析下一步干嘛。

39. 添加数据（Adding data）

数据增强的方法：

• 将现有的例子如何修改或扭曲或使数据更加嘈杂，但在某种程度上，所以你得到的仍然和你的测试集很相似。
  
  
  

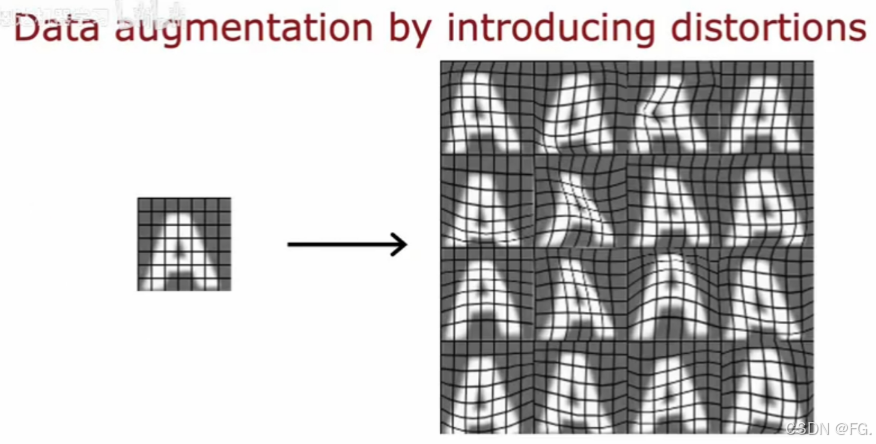
• 数据合成，不是通过修改现有的示例，而是从零开始创造全新的例子。

  把这些字体基本上在文本编辑器中键入随机文本，截图它使用不同的颜色，不同对比度和非常不同的字体，就会得到像右边这样的合成数据。
  

40. 迁移学习：使用其他任务的数据（Transfer learning）

对于一个没有那么多数据的应用程序，迁移技术允许你使用来自不同任务的数据来帮助你的应用程序。

好处：可以使用别人已经通过大量数据集训练好的神经网络模型，只需要自己把输出层替换掉，通过自己的数据去微调神经网络参数，也能得到在你的任务中表现良好的神经网络

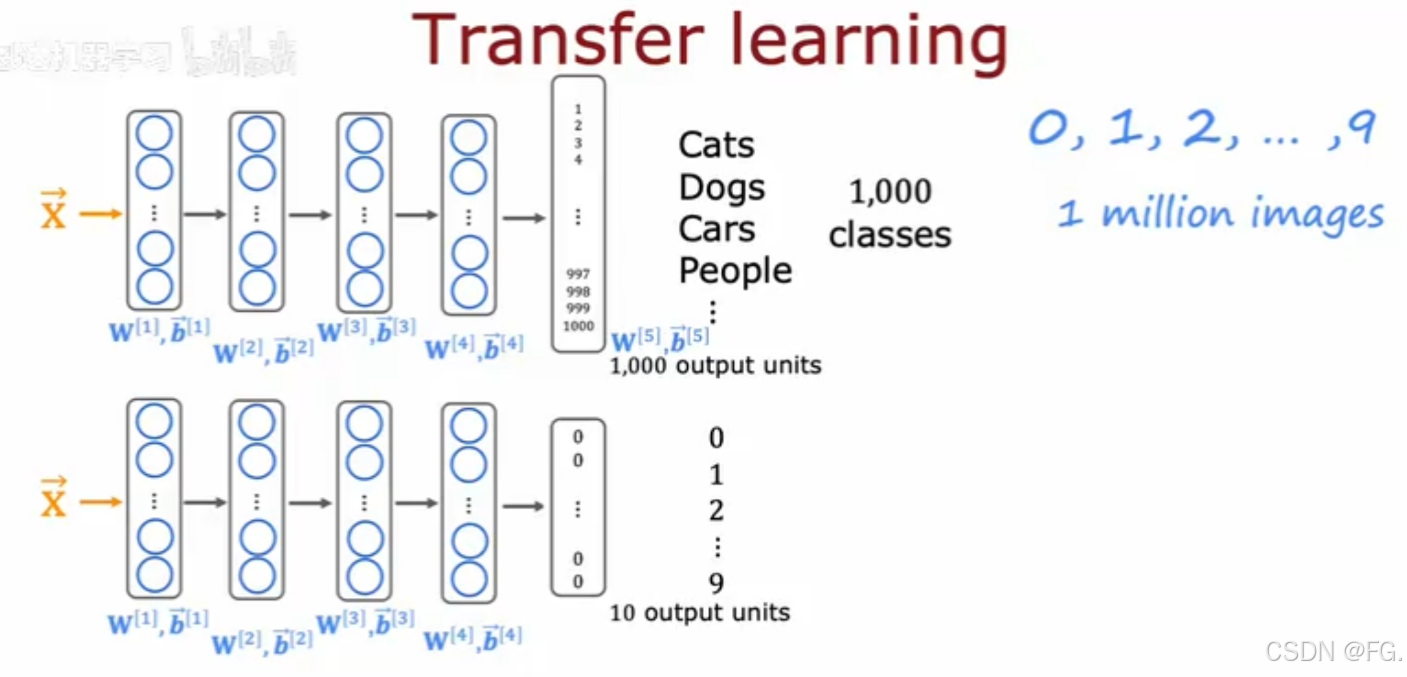
• 只训练输出层参数，适用于0~9数字识别（小训练集）
• 训练网络中的所有参数

41. 倾斜数据集的误差指标（Error metrics for skewed datasets）

在处理倾斜数据集（也称为不平衡数据集）时，传统的误差指标（如准确率）可能无法提供准确的模型性能评估，因为这些指标可能会被多数类的表现主导。为了更好地评估模型在倾斜数据集上的表现，我们需要使用专门的误差指标。

混淆矩阵（Confusion Matrix）：展示了预测结果的详细分布情况，对于二分类任务，它包含以下四个值：

• TP（True Positive）：实际为正类且预测为正类的数量
• TN（True Negative）：实际为负类且预测为负类的数量
• FP（False Positive）：实际为负类且预测为正类的数量
• FN（False Negative）：实际为正类且预测为负类的数量

精确率（Precision）和召回率（Recall）

• 精确率：预测为正类的样本中实际为正类的比例。计算公式为：
  

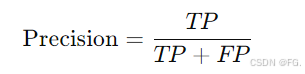
• 召回率：实际为正类的样本中被正确预测为正类的比例。计算公式为：
  

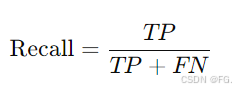
F1-score ：是精确率和召回率的调和平均数，提供了两者的综合评估，适用于类别不平衡的数据集。计算公式为：

• 高F1分数：模型在精确率和召回率之间取得了较好的平衡，这在需要同时关注这两个指标的场景中非常重要。

• 低F1分数：模型在精确率和召回率之间的平衡较差，可能意味着模型整体性能不佳。

42. 精确率和召回率的权衡（Trading off precision and recall）

精确率和召回率通常存在一个权衡关系。提高精确率可能会降低召回率，反之亦然。

• 高精确率，低召回率：模型更保守，只有在非常有把握的情况下才预测为正类。这减少了错误正类（FP），但可能漏掉一些真正的正类（FN）。

• 高召回率，低精确率：模型更宽松，尽可能多地预测正类。这减少了漏掉的正类（FN），但可能增加错误正类（FP）。

在实际应用中，选择适当的指标取决于具体场景：

• 精确率优先：当误报（FP）成本较高时（例如：垃圾邮件过滤，疾病诊断）。
• 召回率优先：当漏报（FN）成本较高时（例如：安全系统，癌症筛查）。

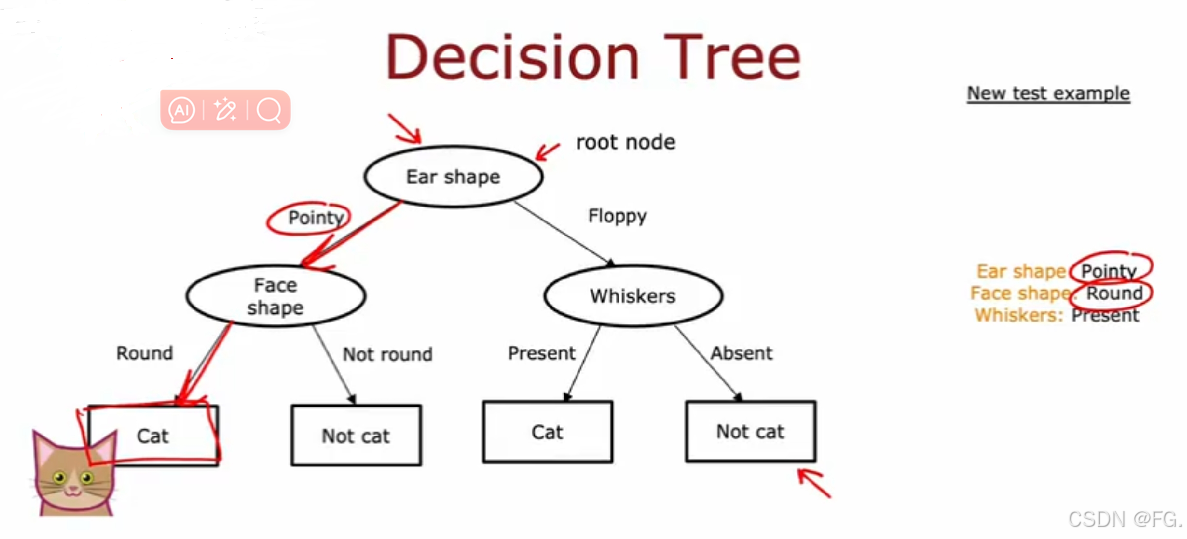
43. 决策树模型（Decision Tree Model）

决策树是一种用于分类和回归任务的非参数监督学习方法。它以树形结构表示决策过程，将数据分割成不同的类别或预测结果。
节点（Node）：

• 根节点（Root Node）：树的顶层节点，包含所有数据。
• 内部节点（Internal Node）：具有一个或多个子节点的节点，用于根据某个特征进行分裂。
• 叶节点（Leaf Node）：不再分裂的节点，表示一个类别或预测值。

边（Edge） ：连接节点的线，表示决策路径。
分裂（Split）：根据某个特征的值将数据集分成子集的过程。

44. 决策树的构建学习过程（Learning Process）

• 选择最佳特征进行分裂。

• 分裂数据集：根据选择的最佳特征，将数据分裂成若干子集。

• 递归构建子树：对每个子集重复以上步骤，直到达到停止条件（如最大深度、最小样本数、一节点的分类纯度达到100%等等）（为了树变小，防止过度拟合）。

45. 测量纯度（Measuring purity）

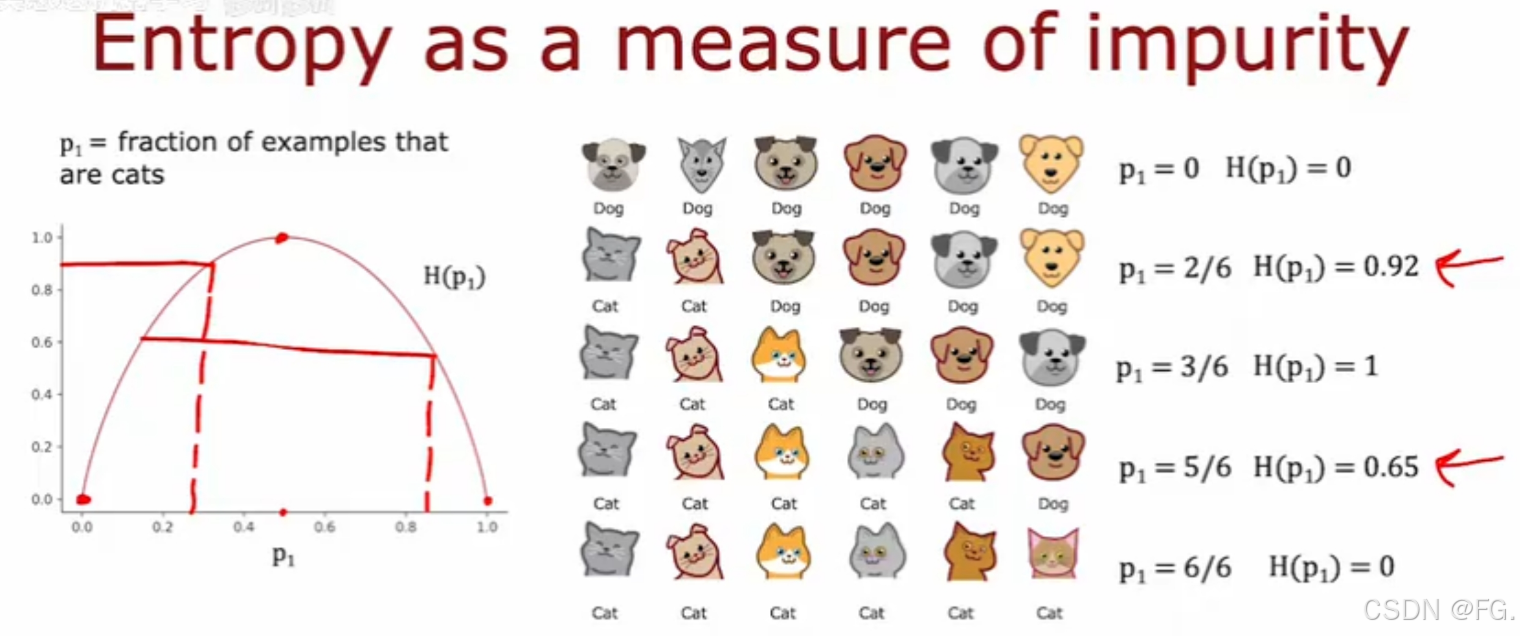
熵（Entropy）用来度量数据集的纯度或不确定性。

• 当所有样本都属于同一类别时，熵为0，表示纯度最高。
• 当样本均匀分布在所有类别时，熵最大，表示混乱度最高。

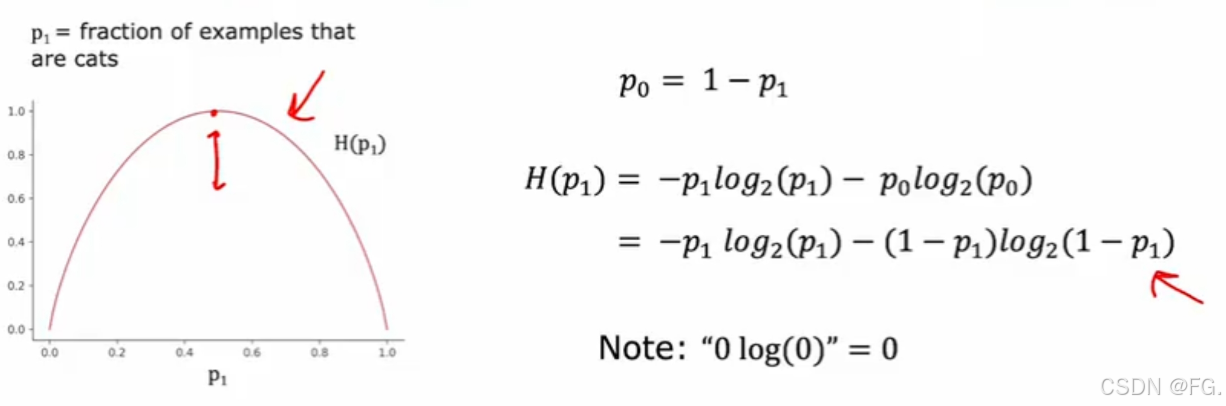
46. 选择拆分信息增益（Information Gain）

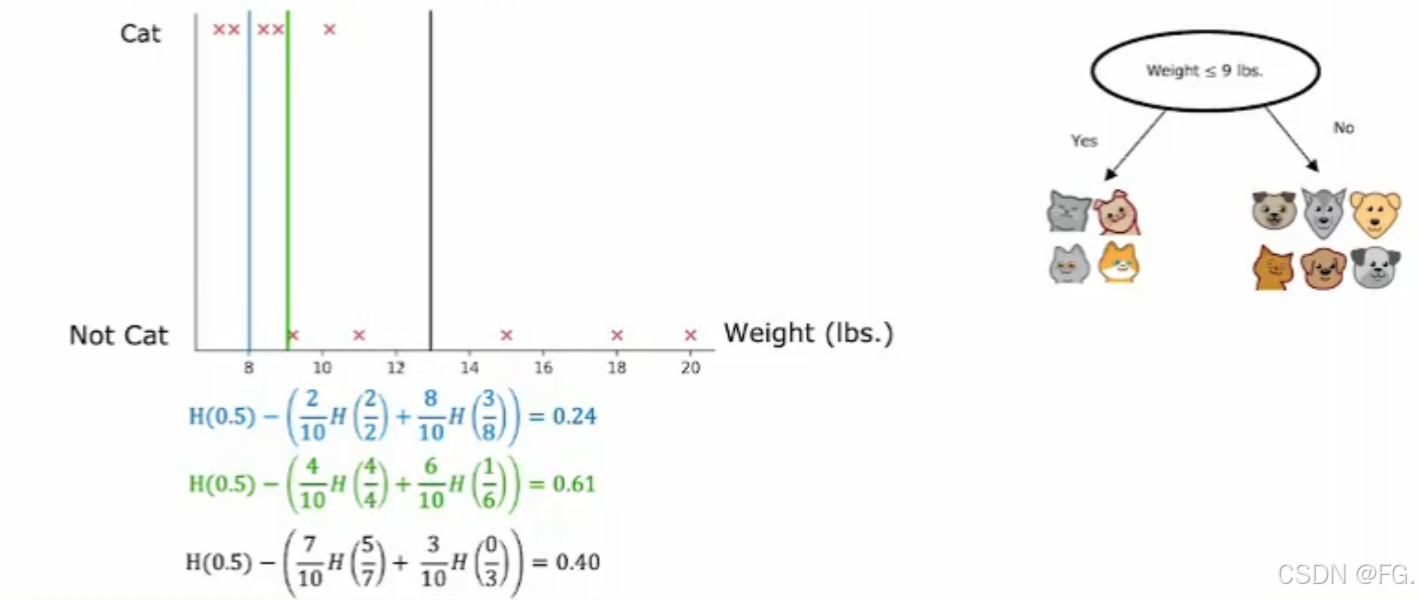
信息增益是基于熵来度量数据的不确定性。信息增益越大，表示使用该特征分裂数据后的纯度提高越多。

47. 使用分类特征的一种独热编码（One-hot Encoding）

如果有特征多个离散值，独热编码是一种将分类特征转换为二进制向量的方法，以便机器学习算法可以处理它们。每个分类特征值都被表示为一个唯一的二进制向量，其中只有一个位置为1，其余位置为0。

独热编码的步骤：

• 识别分类特征的唯一值：找到分类特征中所有可能的值。
• 创建二进制向量：为每个唯一值创建一个二进制向量。
• 转换数据：将每个分类特征值转换为对应的二进制向量。

例如上述表格根据耳朵的特征来创建二进制向量：

• 尖耳朵（pointy ears）--> [1, 0, 0]
• 垂耳朵（Floppy ears）--> [0, 0, 1]
• 圆耳朵（Round ears）--> [0, 1, 0]

48. 连续的有价值特征（Continuous valued features）

如何让决策树与连续值特性一起工作？

决策树通过选择一个最佳的分割点将连续特征转换为离散特征，从而构建树节点。这个分割点可以是特征值的一个阈值，将数据集分成两个子集，一个子集包含小于或等于该阈值的实例，另一个子集包含大于该阈值的实例。

尝试不同的门槛，做通常的信息增益计算，并用选定的阈值对连续值特征进行拆分，如果它给你最好的信息，从所有可能的功能中获得分裂。

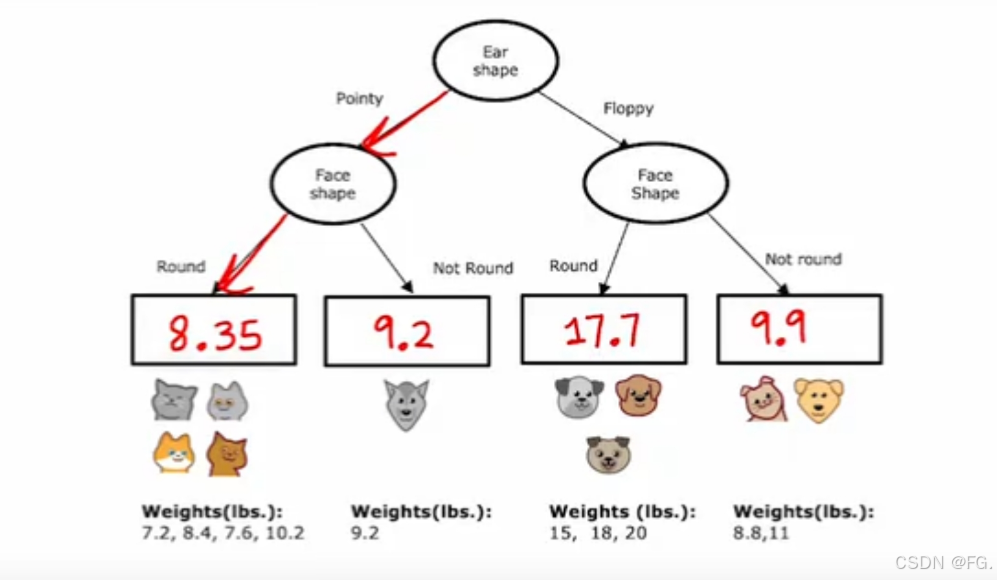
49. 回归树（Regression Tree）

回归树是一种用于回归任务的决策树模型，适用于预测连续值。与分类树不同，回归树的目标是预测一个数值输出，而不是分类标签。回归树通过分割数据并建立模型，使得每个叶节点包含相对均匀的数据，以最小化预测误差。

• 分割数据：：回归树通过选择最佳分割点将数据集分割成若干子集。每次分割选择一个特征及其相应的值，使得分割后的子集的目标变量方差最小。
• 叶节点值：每个叶节点的值是其包含的训练数据目标值的平均值或中位数。
• 损失函数：回归树使用均方误差（MSE）或均绝对误差（MAE）作为损失函数来评估分割质量。

构建过程：

• 选择分割点：对于每个特征，尝试不同的分割点，选择使得分割后的子集的目标。
• 递归分割：在每个子集中重复上述过程，直到满足停止条件。
• 生成叶节点：当满足停止条件时，生成叶节点，其值为子集目标变量的平均值或中位数。

使用多个决策树的技术被称为集成学习（Ensemble Learning），其目标是通过组合多个基模型的预测来提高整体模型的性能和稳定性。

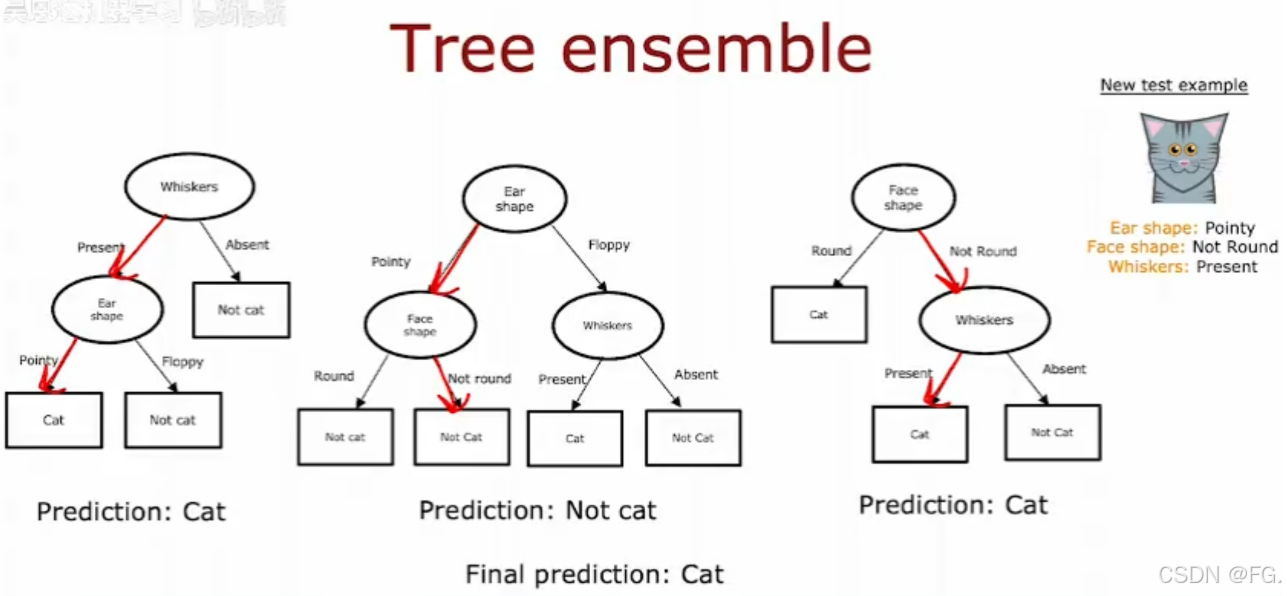
50. 随机森林算法（Random forest algorithm）

随机森林（Random Forest）是一种流行的集成学习方法，用于分类和回归任务。它通过构建多个决策树，并结合这些树的预测结果来提高模型的准确性和鲁棒性。随机森林的关键思想是利用放回抽样和随机特征选择，构建一组相对独立的决策树模型。

• 数据集的放回抽样：从原始数据集中随机抽取多个自助样本（bootstrap samples），每个样本集与原始数据集大小相同，允许重复抽取。
• 训练决策树：对每个自助样本集，构建一棵决策树。在构建树的过程中，每个节点分裂时随机选择一部分特征（而不是使用所有特征），然后从中选择最佳分割特征。
• 组合预测：对于分类任务，随机森林通过对所有树的预测结果进行投票，选择出现次数最多的类别作为最终预测。对于回归任务，随机森林通过对所有树的预测结果取平均值作为最终预测。

随机森林的优点

• 减少过拟合：通过组合多棵树的预测结果，随机森林减少了单个决策树的过拟合问题。
• 鲁棒性和准确性：随机森林对数据噪声和异常值具有较好的鲁棒性，并且通常具有较高的预测准确性。
• 处理高维数据：随机森林可以有效处理高维数据（即具有大量特征的数据集）。

随机森林的缺点

• 计算成本较高：由于需要训练大量的决策树，随机森林的训练时间和计算成本较高。
• 模型解释性较差：随机森林是一个"黑盒"模型，相比单棵决策树，难以解释和理解。

示例：使用随机森林算法进行分类任务，使用鸢尾花数据集（Iris dataset），包含三类不同的鸢尾花（setosa、versicolor、virginica），每类50个样本，每个样本有四个特征（花萼长度、花萼宽度、花瓣长度和花瓣宽度），取30%作为测试集，70%作为训练集。

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, classification_report

# 1. 加载数据集
iris = load_iris()
x, y = iris.data, iris.target

# 2. 数据预处理（本例中数据已预处理完毕）

# 3. 划分训练集和测试集
random_seed = 42  # 设置随机种子以确保结果可重复
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=random_seed)

# 4. 训练随机森林模型
rf_classifier = RandomForestClassifier(n_estimators=100, random_state=random_seed)
rf_classifier.fit(x_train, y_train)

# 5. 评估模型性能
y_pred = rf_classifier.predict(x_test)
accuracy = accuracy_score(y_test, y_pred)
report = classification_report(y_test, y_pred, target_names=iris.target_names)

print(f'Accuracy: {accuracy:.2f}')
print('Classification Report:')
print(report)

各项指标达到100%，模型性能非常好。

51. XGBoost算法

XGBoost（Extreme Gradient Boosting）是一种高效的梯度提升算法，广泛应用于机器学习竞赛和实际项目中。它基于梯度提升决策树（GBDT），通过添加正则化项来防止过拟合，同时在速度和效率上进行了优化。

XGBoost的基本思想是通过集成多个弱学习器（如决策树），逐步减小训练误差。每一轮迭代中，模型尝试拟合前一轮的残差，逐步逼近真实值。

import xgboost as xgb
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report

# 1. 数据准备
iris = load_iris()
x, y = iris.data, iris.target

# 2. 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=42)

# 3. 转换为DMatrix对象
dtrain = xgb.DMatrix(x_train, label=y_train)
dtest = xgb.DMatrix(x_test, label=y_test)

# 4. 设置参数
params = {
    'booster': 'gbtree',           # 使用的提升模型
    'objective': 'multi:softmax',  # 多分类问题
    'num_class': 3,                # 类别数
    'eta': 0.3,                    # 学习率
    'max_depth': 6,                # 树的最大深度
    'gamma': 0,                    # 最小损失减少
    'subsample': 0.8,              # 样本采样比例
    'colsample_bytree': 0.8,       # 特征采样比例
    'seed': 42                     # 随机种子
}

# 5. 训练模型
num_round = 100   # 迭代次数
bst = xgb.train(params, dtrain, num_round)

# 6. 预测
y_pred = bst.predict(dtest)

# 7. 模型评估
accuracy = accuracy_score(y_test, y_pred)
report = classification_report(y_test, y_pred, target_names=iris.target_names)

print(f'Accuracy: {accuracy:.2f}')
print('Classification Report:')
print(report)

52. 什么时候使用决策树（when to use decision tree）

• 决策树和树集成适用于表格（结构化）数据，不建议用于非结构化数据（图像、音频、文本）
• 神经网络适用于所有类型的数据，包括表格(结构化)和非结构化数据。

53. 什么是聚类（Clustering）

聚类（Clustering）是一种无监督学习方法，其目的是将数据集中的对象根据相似性进行分组，使得同一组内的对象彼此相似，而不同组之间的对象差异显著。这种方法在许多领域都有广泛应用，例如图像处理、市场分析、社交网络分析和生物信息学等。

簇（Cluster）：一个簇是指一组相似的数据点，这些数据点在某些方面具有相似的特性或属性。

中心点（Centroid）：指簇的中心位置，通常用来代表该簇中的所有点。在 K-means 聚类算法中，中心点是质心。

距离度量（Distance Metric）：衡量数据点之间相似性的一种方式。常用的距离度量方法包括欧氏距离、曼哈顿距离、余弦相似度等。

54. K-means 算法

K-means 算法是一种经典的聚类算法，旨在将数据集划分为 K 个簇，使得同一簇内的数据点尽可能相似，而不同簇的数据点尽可能不同。K-means是一种迭代算法，通过不断优化簇的质心位置来最小化簇内的方差。

• 初始化：选择 K 个初始质心，可以随机选择数据点或使用其他方法（比如 K-means++）。
• 分配簇：对于数据集中每个点，计算其到每个质心的距离，并将其分配给最近的质心。
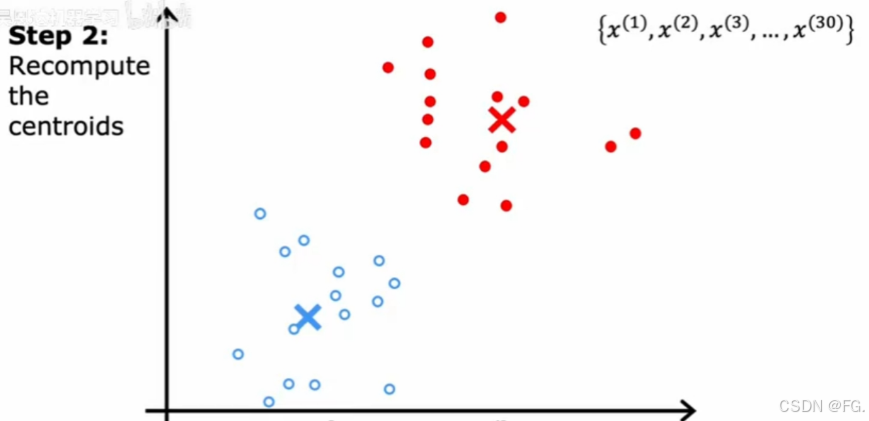
• 更新质心：对于每个簇，计算簇内所有点的平均值，并将质心移动到这个平均值位置。
• 重复步骤2和3：不断迭代，直到质心位置不再变化或达到预设的最大迭代次数。
  
  
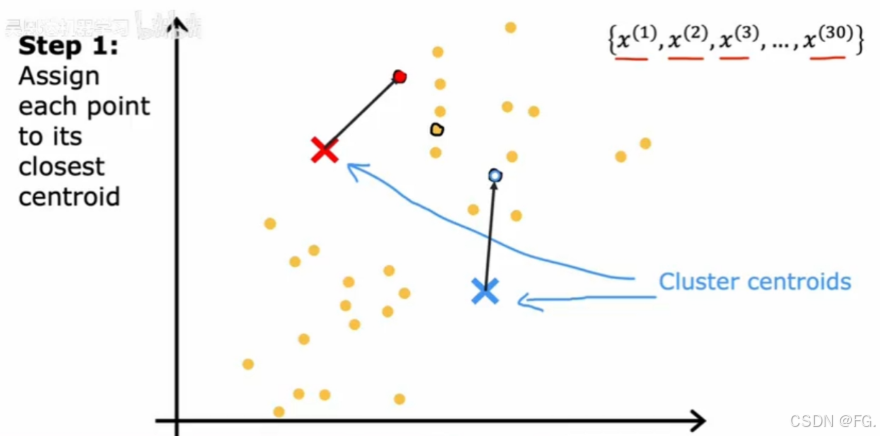
  不断迭代，直到质心不再变化。
  

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

# 生成示例数据
np.random.seed(42)
x = np.random.rand(100, 2)

# 选择 K 值
k = 3

# 初始化 K-means 模型，默认随机初始化
kmeans = KMeans(n_clusters=k, random_state=42)

# 训练模型
kmeans.fit(x)

# 获取聚类结果
labels = kmeans.labels_
centroids = kmeans.cluster_centers_

# 可视化聚类结果
plt.scatter(x[:, 0], x[:, 1], c=labels, cmap='viridis', marker='o')
plt.scatter(centroids[:, 0], centroids[:, 1], s=300, c='red', marker='x')
plt.title('K-means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()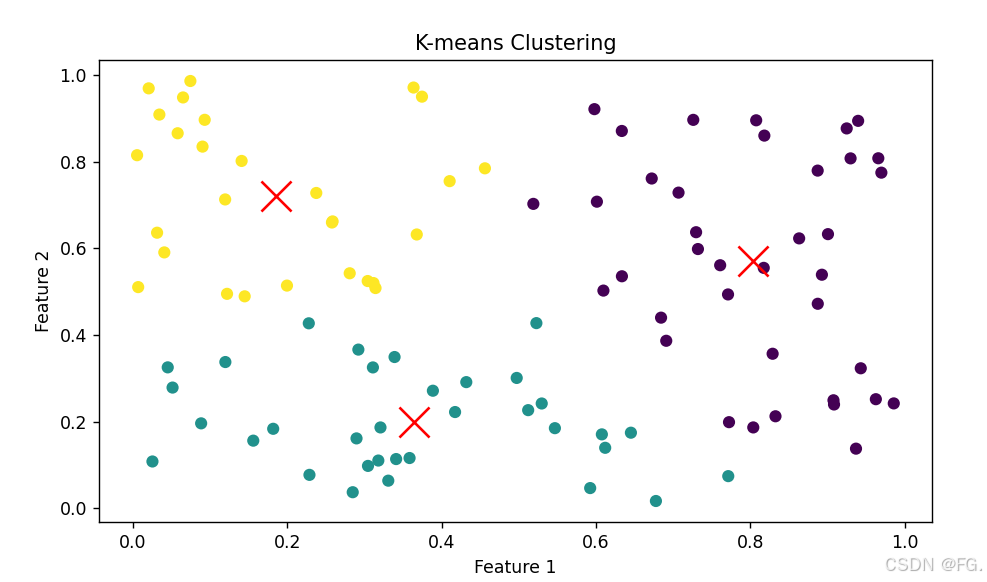

55. K-means 成本函数（Cost Function）

K-means 聚类的成本函数通常被称为"簇内平方和误差"（Within-Cluster Sum of Squares, WCSS）或"簇内平方误差"（Sum of Squared Errors, SSE）。该成本函数用于衡量数据点与其所在簇质心之间的距离，目标是通过最小化该成本函数来优化簇划分。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

# 生成示例数据
np.random.seed(42)
x = np.random.rand(100, 2)

# 设置 K 值
k = 3

# 使用 K-means 聚类，这里使用 k-means++初始化
kmeans = KMeans(n_clusters=k, init='k-means++', random_state=42)
kmeans.fit(x)

# 获取聚类结果
labels = kmeans.labels_
centroids = kmeans.cluster_centers_

# 计算成本函数（WCSS）
wcss = 0
for i in range(k):
    cluster_points = x[labels == i]
    centroid = centroids[i]
    wcss += np.sum((cluster_points - centroid) ** 2)

print(f'WCSS (Within-Cluster Sum of Squares): {wcss}')

# 可视化聚类结果
plt.scatter(x[:, 0], x[:, 1], c=labels, cmap='viridis', marker='o')
plt.scatter(centroids[:, 0], centroids[:, 1], s=300, c='red', marker='x')
plt.title('K-means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

• 随机初始化：简单但可能导致不稳定的结果，收敛速度较慢。
• K-means++ 初始化：通过选择相距较远的点作为初始质心，提高了聚类结果的质量和收敛速度，是实际应用中最常用的方法。

56. 选择聚类的个数 K （Choosing the number of clusters）

如何选择正确的 K 值？

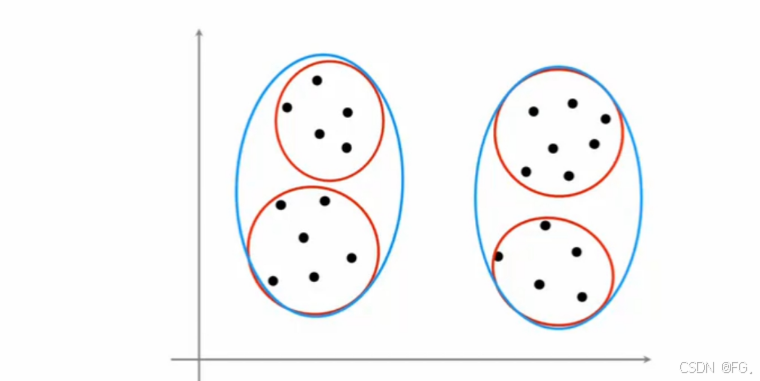
肘部法则（Elbow Method）:肘部法则通过绘制不同 K 值对应的 SSE（Sum of Squared Errors）或 WCSS（Within-Cluster Sum of Squares）曲线，寻找曲线的"肘部"位置，即拐点，作为最优的 K 值。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

# 生成示例数据
np.random.seed(42)
x = np.random.rand(100, 2)

# 计算不同 K 值的 SSE
sse = []
k_values = range(1, 11)
for k in k_values:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(x)
    sse.append(kmeans.inertia_)

# 绘制 SSE 曲线
plt.plot(k_values, sse, '-o')
plt.xlabel('Number of clusters (k)')
plt.ylabel('Sum of squared errors (SSE)')
plt.title('Elbow Method for Optimal k')
plt.show()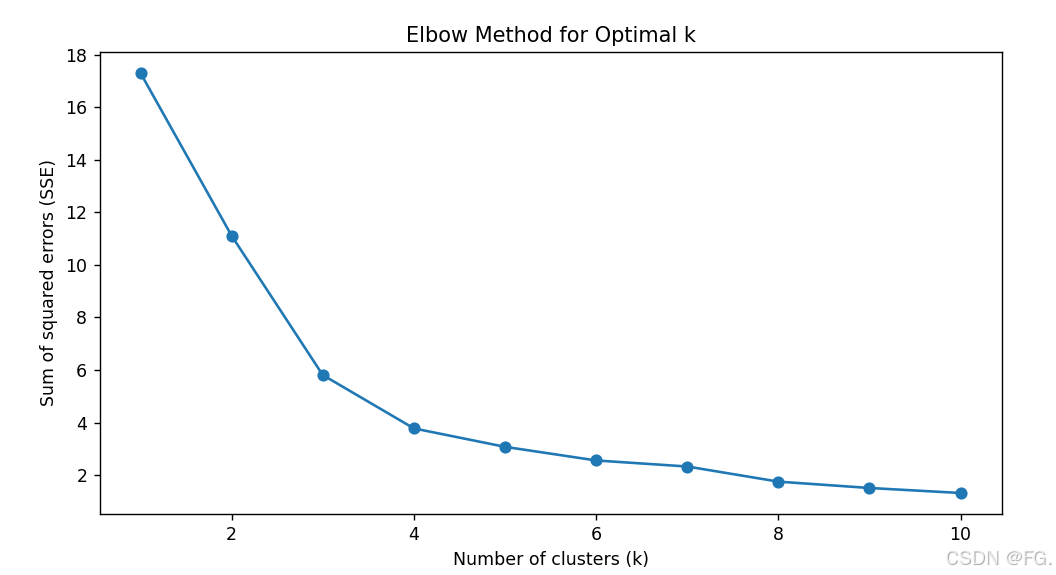

在绘制的曲线中，寻找曲线开始平缓的拐点位置作为最优的 K 值。

图表解释对应K=3 和 K=4 的 SSE 值分别是：

• K=3: SSE = 5.81
• K=4: SSE = 3.76

根据肘部法则，最优的 K 值通常位于拐点位置。在这个图中，拐点位置似乎在

K=3 和 K=4 之间。因此，可以认为最优的 K 值是 3 或 4。具体选择哪个取决于你对聚类紧凑性的需求。如果需要更紧凑的聚类，可以选择 K=4；如果需要更少的簇，可以选择 K=3。

总的来说，依据肘部法则，最优的 K 值为 3 或 4。 ​

轮廓系数（Silhouette Score） ：

轮廓系数通过计算每个样本的轮廓系数（Silhouette Coefficient），评估不同 K 值下的聚类质量。轮廓系数取值范围为 -1 到 1，值越高表示聚类效果越好。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score

# 生成示例数据
np.random.seed(42)
x = np.random.rand(100, 2)

# 计算不同 K 值的轮廓系数
silhouette_scores = []
k_values = range(2, 11)
for k in k_values:
    kmeans = KMeans(n_clusters=k, init='k-means++', random_state=42)
    kmeans.fit(x)
    labels = kmeans.labels_
    silhouette_scores.append(silhouette_score(x, labels))

# 绘制轮廓系数曲线
plt.plot(k_values, silhouette_scores, '-o')
plt.xlabel('Number of clusters (k)')
plt.ylabel('Silhouette Score')
plt.title('Silhouette Score for Optimal k')
plt.show()

# 找到轮廓系数最高的K值
optimal_k = k_values[np.argmax(silhouette_scores)]
print(f"The optimal number of clusters (k) is: {optimal_k}")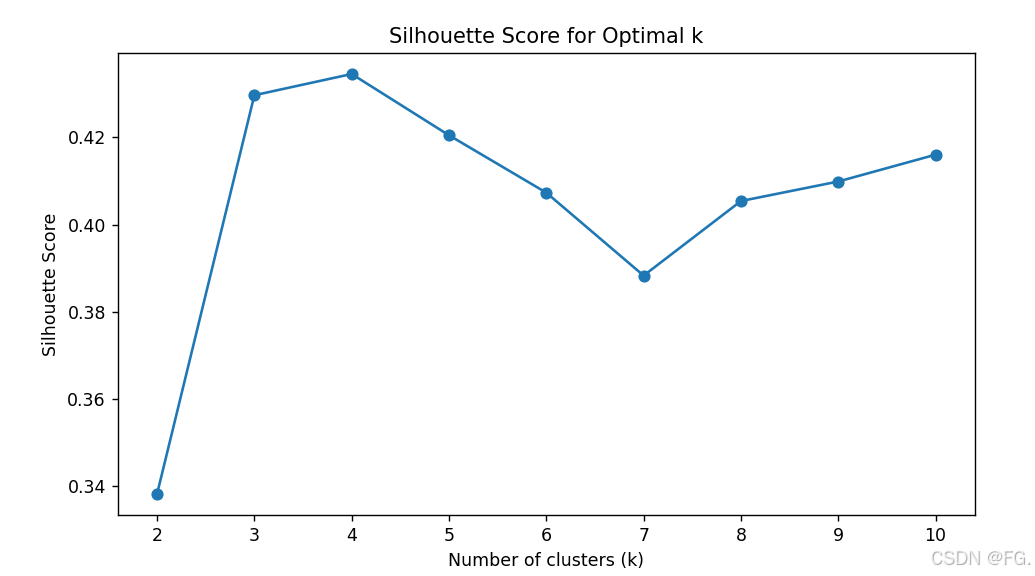

在绘制的曲线中，选择轮廓系数最高的 K 值作为最优的 K 值。

57. 高斯（正态）分布（Gaussion Distribution）

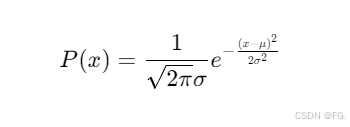
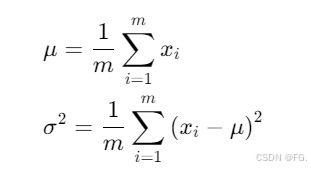
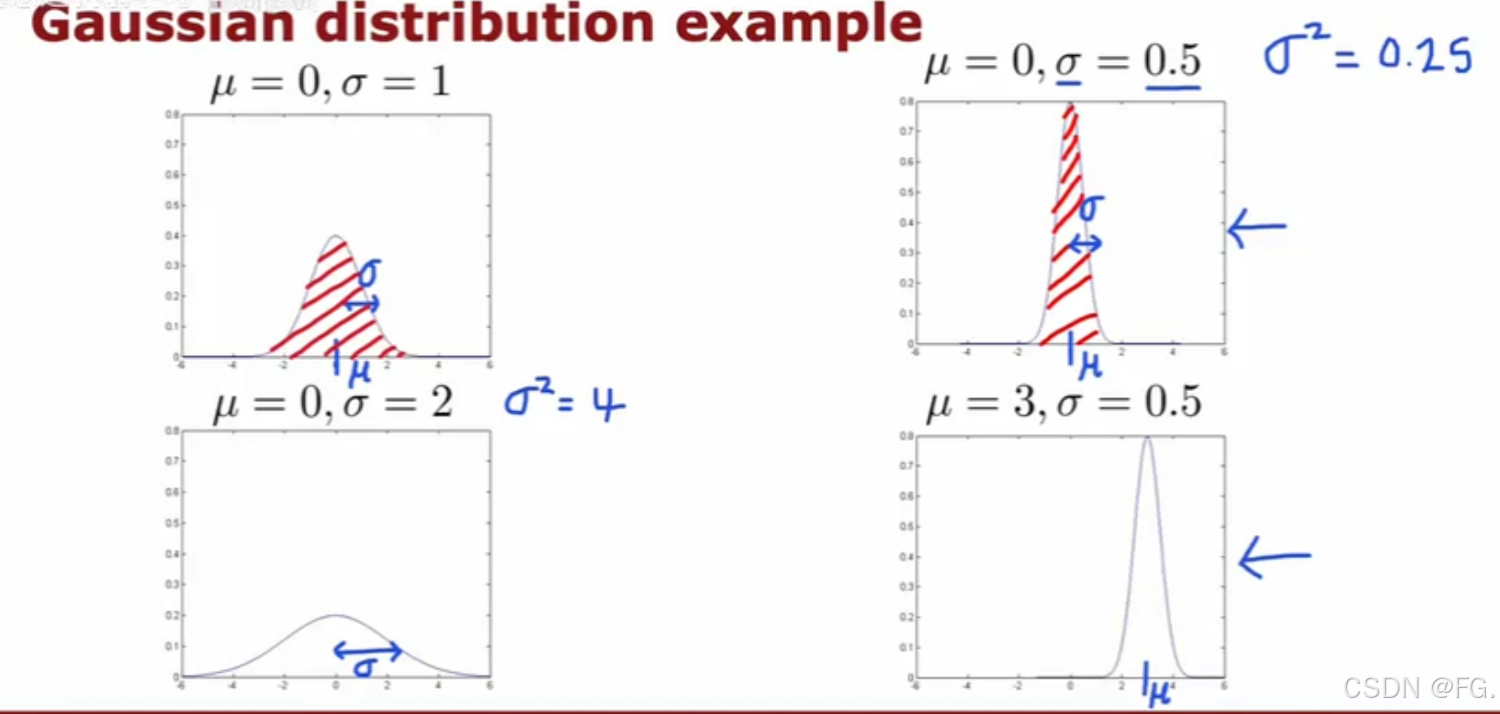
下面是样本方差，对于样本数据（而非总体数据），分母是 m-1，这是因为样本方差需要调整自由度。

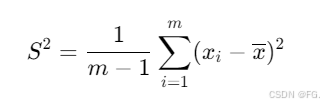
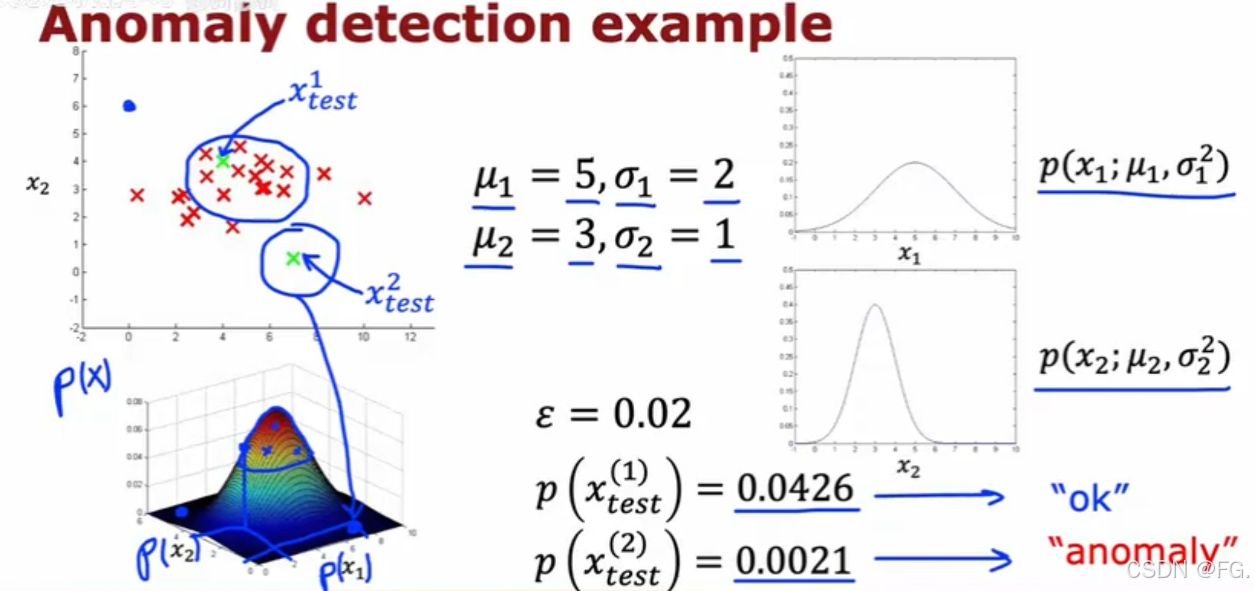
58. 异常检测算法（Anomaly detection algorithm）

异常检测算法用于识别数据集中不同于其他数据的异常或异常值。

59. 异常检测VS监督学习（Anomaly detection vs supervised learning）

1. 数据量和标签可用性：如果有充足的标签数据且各类样本分布均衡，优先考虑监督学习。如果标签数据稀少或不存在，优先考虑异常检测。
2. 实时性和复杂度：实时性要求高且数据模式变化快，异常检测更合适。复杂问题且有稳定标签数据，监督学习更能提供精确的结果。
3. 业务需求和目标：确定业务目标，选择最能满足需求的方法。有时可以结合使用，例如先用异常检测识别潜在异常，再用监督学习分类已知类别。

60. 协同过滤算法（Collaborative filtering algorithm）

协同过滤是一种常用于推荐系统的算法，通过利用用户行为数据（如用户的评分、浏览历史、购买记录等）来推荐用户可能感兴趣的项目。协同过滤主要分为两类：基于用户的协同过滤（User-Based Collaborative Filtering）和基于项目的协同过滤（Item-Based Collaborative Filtering）。

（1）基于用户的协同过滤（User-Based Collaborative Filtering） ：

用户的协同过滤是一种推荐系统技术，它通过分析用户之间的相似性，来为用户推荐他们可能感兴趣的物品。

• 构建用户 --- 物品评分矩阵：收集用户对物品的评分数据，形成一个矩阵。
• 计算用户相似度：使用相似度度量方法（如皮尔逊相关系数或余弦相似度）计算用户之间的相似度。
• 推荐物品：根据相似用户的评分，预测当前用户未评分物品的评分，并推荐评分最高的物品。

import pandas as pd
import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.metrics.pairwise import cosine_similarity

# 创建用户-电影评分矩阵
data = {
    '电影1': [4, np.nan, 4, 3, 5],
    '电影2': [np.nan, 2, 3, 5, 4],
    '电影3': [3, 4, 4, 4, np.nan],
    '电影4': [5, 3, 2, 4, 3],
    '电影5': [1, 5, np.nan, 2, 3]
}
df = pd.DataFrame(data, index=['用户A', '用户B', '用户C', '用户D', '用户E'])

# 打印用户-电影评分矩阵
print('用户-电影评分矩阵：')
print(df)

# 计算用户之间的余弦相似度
user_similarity = cosine_similarity(df.fillna(0))

# 创建用户相似度矩阵
similarity_matrix = pd.DataFrame(user_similarity, index=df.index, columns=df.index)

# 打印用户相似度矩阵
print('\n用户相似度矩阵：')
print(similarity_matrix)

# 为用户A推荐电影
target_user = '用户A'
neighbors = similarity_matrix[target_user].nlargest(3).drop(target_user).index  # 找到相似度最高的两个邻居

# 打印邻居用户
print('\n邻居用户：')
print(neighbors)

# 计算推荐电影的预测评分
def predict_rating(user, item):
    sim_scores = similarity_matrix.loc[user, neighbors]
    ratings = df.loc[neighbors, item].fillna(0)
    return np.dot(sim_scores, ratings) / sim_scores.sum()


# 找到用户A未评分的电影
# 使用了布尔索引，也称为掩码（masking）返回的布尔 Series 被用来筛选 df.loc[target_user] 中的元素。
unrated_items = df.loc[target_user][df.loc[target_user].isna()].index

# 打印用户A未评分的电影
print('\n用户A未评分的电影：')
print(unrated_items)

# 计算每个未评分电影的预测评分
predictions = {item: predict_rating(target_user, item) for item in unrated_items}

# 打印预测评分
print('\n预测评分：')
print(predictions)

# 给用户A推荐评分最高的电影
recommended_item = max(predictions, key=predictions.get)
print(f'\n推荐给{target_user}的电影是：{recommended_item}，预测评分是：{predictions[recommended_item]:.2f}')

# 计算 MSE 均方误差
actual_ratings = [3]  # 假设用户A对电影2的实际评分为3
predicted_ratings = [predictions[item] for item in unrated_items]
mse = mean_squared_error(actual_ratings, predicted_ratings)
print(f'MSE：{mse:.2f}')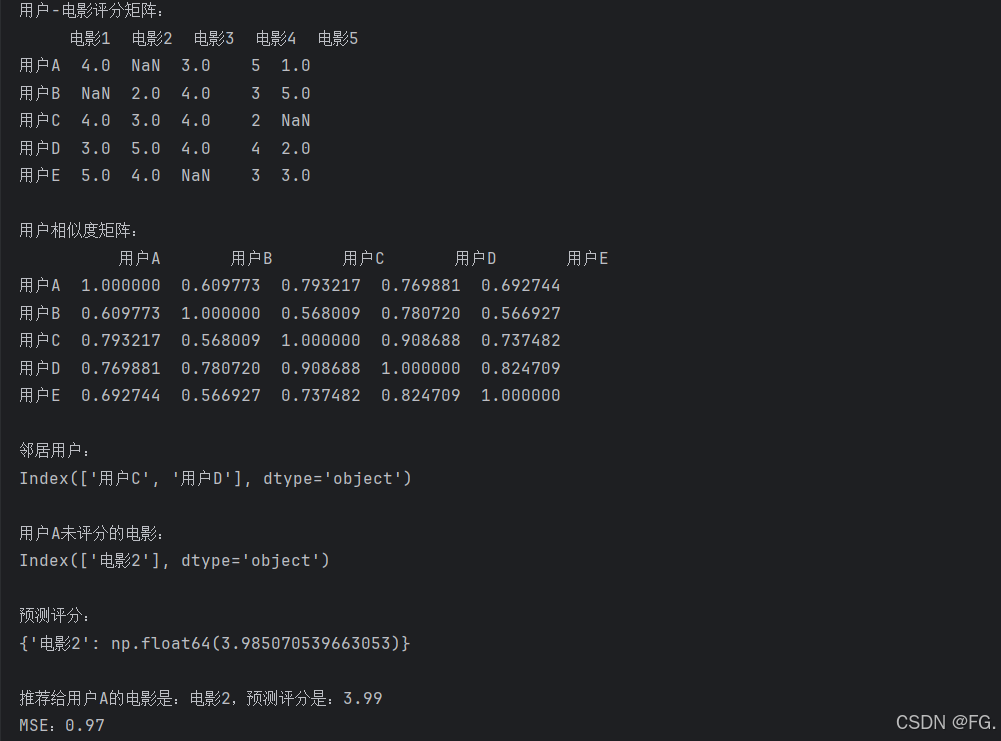

成本函数：在基于用户的协同过滤中，成本函数（也称为损失函数）用于衡量预测评分与实际评分之间的差异。

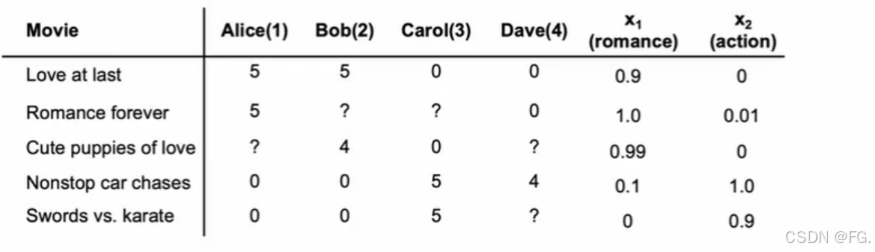
以用户评分电影为例子：

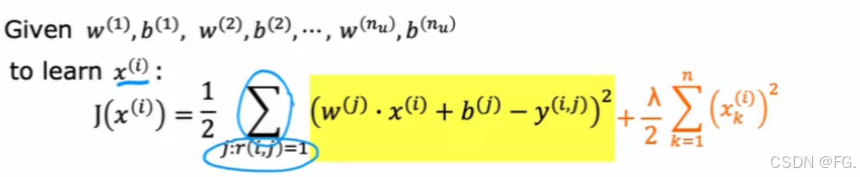
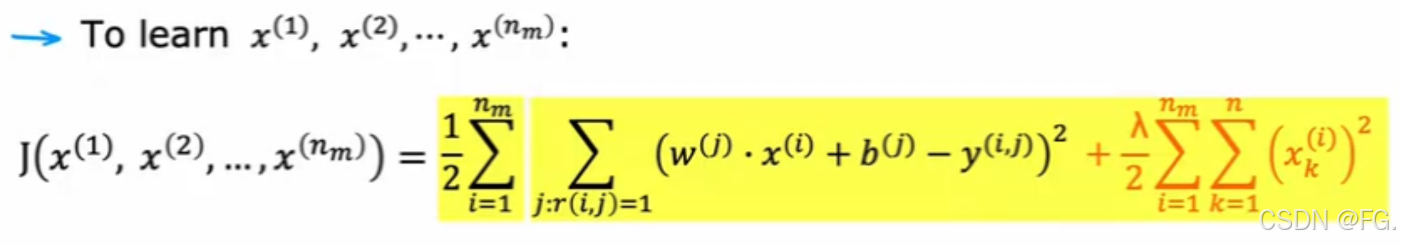
损失函数为：

梯度下降：

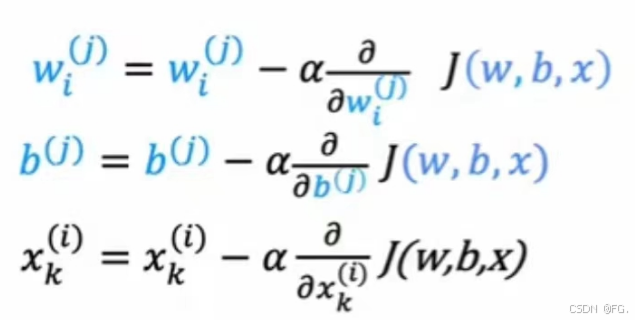
（2）基于内容的协同过滤（Content-Based Collaborative Filtering）：基于内容的协同过滤是一种推荐系统算法，通过比较项目的属性（例如，电影的类型、导演、演员等）来进行推荐。它假设如果用户喜欢某个项目，他们也会喜欢具有类似属性的其他项目。

可通过电影的特征和用户对电影的评价来构建神经网络：

import pandas as pd
from sklearn.metrics.pairwise import cosine_similarity

# 创建电影属性矩阵
data = {
    '电影': ['电影1', '电影2', '电影3', '电影4', '电影5'],
    '类型_动作': [1, 0, 1, 0, 0],
    '类型_喜剧': [0, 1, 0, 1, 0],
    '类型_剧情': [0, 0, 0, 1, 1],
    '导演_A': [1, 0, 0, 1, 0],
    '导演_B': [0, 1, 1, 0, 0],
    '演员_X': [1, 0, 1, 0, 1],
    '演员_Y': [0, 1, 0, 1, 0]
}

df_movies = pd.DataFrame(data)
print(df_movies)
df_movies.set_index('电影', inplace=True)
print('电影属性矩阵：')
print(df_movies)

# 计算电影之间的余弦相似度
movie_similarity = cosine_similarity(df_movies)
similarity_matrix = pd.DataFrame(movie_similarity, index=df_movies.index, columns=df_movies.index)
print('电影相似度矩阵：')
print(similarity_matrix)

# 用户喜欢的电影
user_likes = ['电影1', '电影3']

# 计算电影与用户喜欢的电影的平均相似度
recommendation_scores = similarity_matrix[user_likes].mean(axis=1)
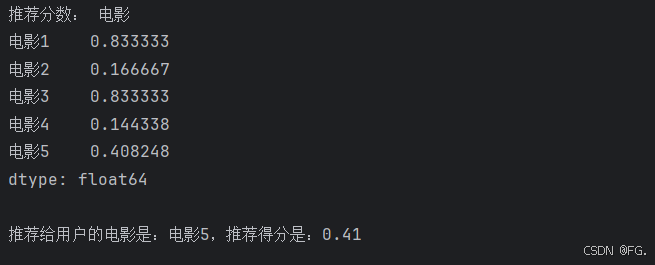
print('推荐分数：', recommendation_scores)

# 移除用户已经看过的电影
recommendation_scores = recommendation_scores.drop(user_likes)

# 推荐得分最高的电影
recommended_movie = recommendation_scores.idxmax()
print(f"\n推荐给用户的电影是：{recommended_movie}，推荐得分是：{recommendation_scores[recommended_movie]:.2f}")

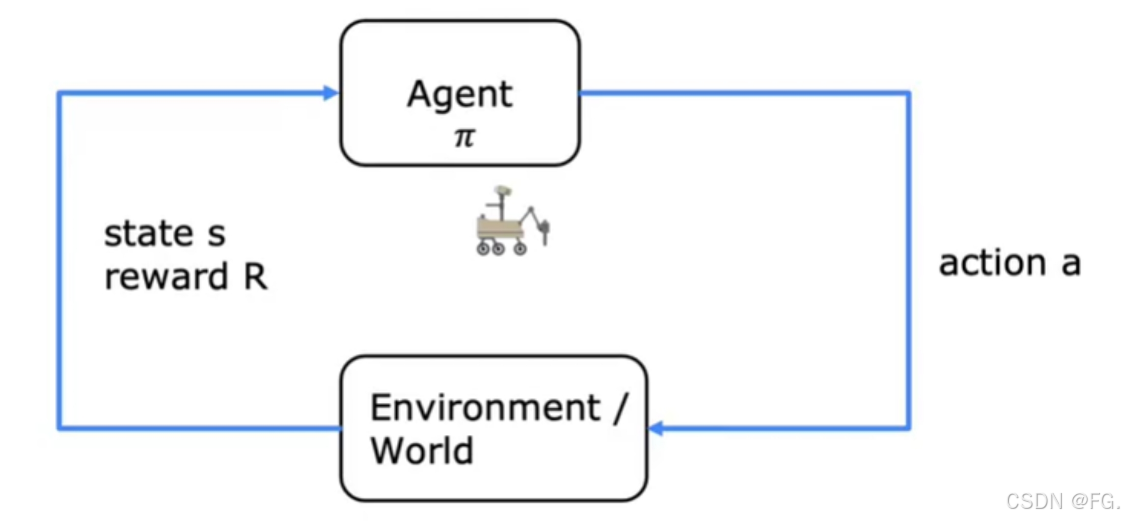
61. 强化学习（Reinforcement Learning）

强化学习（RL）是一种机器学习范式，其中智能体（agent）通过与环境（environment）的交互来学习如何采取行动，以最大化某个累积奖励（cumulative reward）。在强化学习中，智能体通过试错的方式探索环境，并根据获得的奖励来调整其策略。

• 智能体（Agent）：做出决策的主体，尝试通过与环境交互来达到某个目标。

• 环境（Environment）：智能体所处的世界，智能体在其中采取行动并接收反馈（奖励或惩罚）。

• 状态（State, S）：环境在某个时刻的具体情况，可以通过某些特征或变量来描述。

• 动作（Action, A）：智能体在每个状态下采取的行为。

• 奖励（Reward, R）：智能体采取某个动作之后，环境给予的反馈信号，用于指导智能体的学习过程。

• 策略（Policy, π）：智能体选择动作的规则或方法，可以是确定性的（deterministic）或随机性的（stochastic）。

• 折现因子（Discount Factor, γ）：
  

• 值函数（Value Funciton, V）：估计某个状态或状态---动作对的长期累积奖励。

• Q值函数（Q-Value Function, Q）：估计在某个状态下采取某个动作的长期累积奖励。

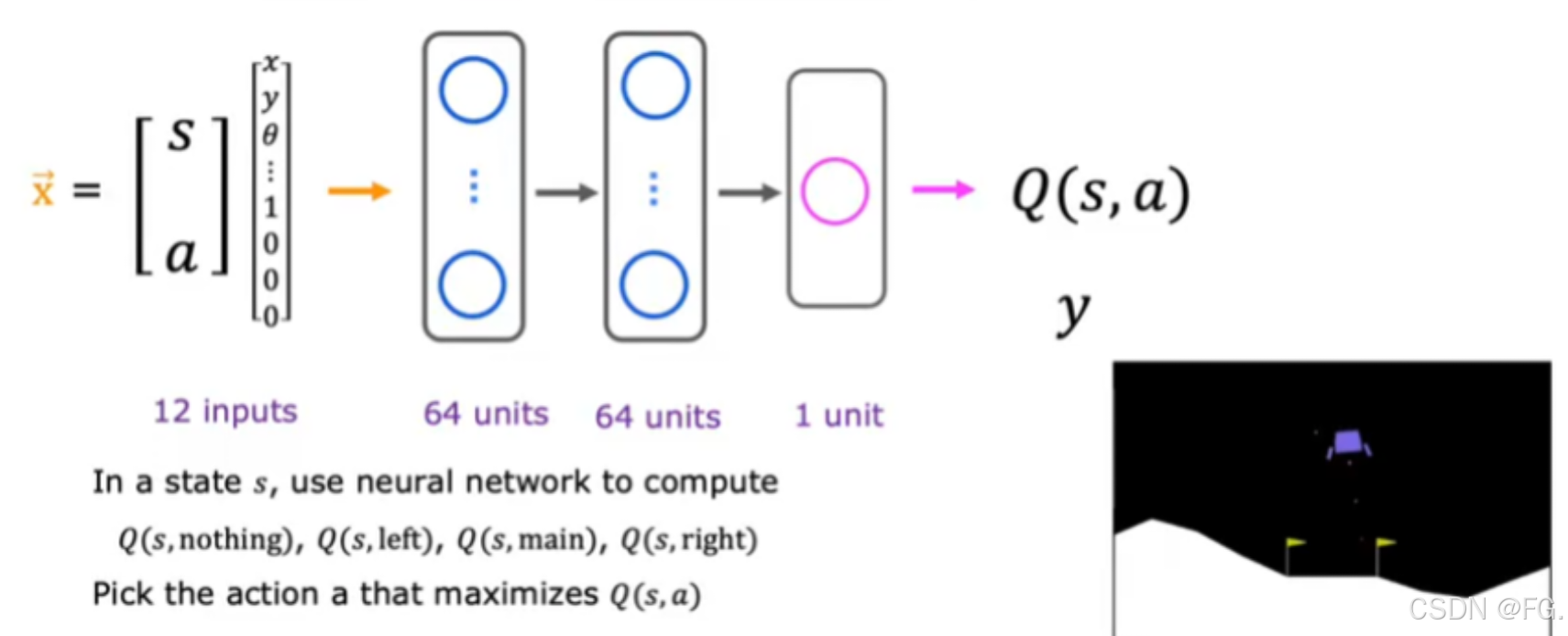
62. 状态动作值函数（State-action value function）

状态动作值函数通常用 Q(s,a) 表示，它表示在某个状态 s 下采取某个动作 a 所能获得的预期累计奖励。

63. Bellman方程（Bellman Equation）

用于描述状态值函数（或者动作值函数）之间的关系。它基于以下基本思想：一个状态（或动作）的值可以通过后续状态（或动作）的值递归定义。

s：当前的状态值

a：当前的动作

s'：下一步的状态值

a'：下一步的动作

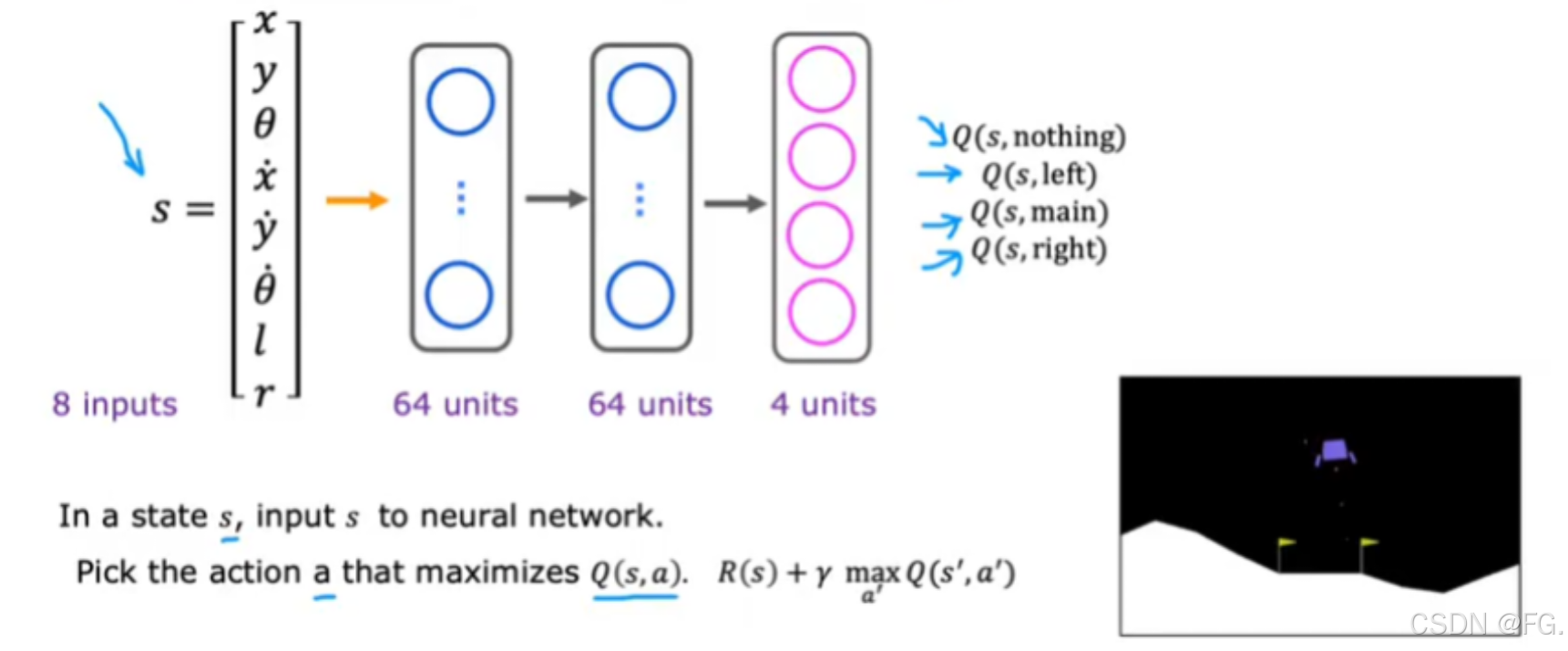
64. 学习状态值函数的神经结构（Learning the state-value function）

65. 算法优化--- ϵ-贪婪策略

这种策略在选择动作时既有一定的探索性（随机选择动作），又有一定的利用性（选择当前 Q 值最大的动作），从而平衡了探索和利用。

• 贪婪选择：选择当前 Q 值最大的动作。
• 随机选择：以 ϵ 的概率随机选择一个动作。

import numpy as np


# 创建简化的环境，只能左右移动
class SimpleGridWorld:
    def __init__(self, size=5):
        self.size = size
        self.state = 0  # 初始状态
        self.goal = size - 1  # 目标状态
        self.actions = ['left', 'right']

    def reset(self):
        self.state = 0
        return self.state

    def step(self, action):
        if action == 'left':
            self.state = max(self.state - 1, 0)
        elif action == 'right':
            self.state = min(self.state + 1, self.size - 1)

        if self.state == self.goal:
            return self.state, 1, True  # 到达目标，奖励1，结束
        else:
            return self.state, -0.01, False  # 非目标，轻微惩罚，继续


# Q-Learning 参数
alpha = 0.1  # 学习率
gamma = 0.99  # 折现因子
epsilon = 0.1  # 探索概率
num_episodes = 500

# 初始化 Q 表
Q = {}
for state in range(5):
    Q[state] = {a: 0 for a in ['left', 'right']}

# 训练
env = SimpleGridWorld()

for episode in range(num_episodes):
    state = env.reset()
    done = False

    while not done:
        # 选择动作
        if np.random.rand() < epsilon:
            action = np.random.choice(env.actions)
        else:
            action = max(Q[state], key=Q[state].get)

        # 执行动作
        next_state, reward, done = env.step(action)

        # 更新 Q 值
        best_next_action = max(Q[next_state], key=Q[next_state].get)
        td_target = reward + gamma * Q[next_state][best_next_action]
        Q[state][action] += alpha * (td_target - Q[state][action])

        state = next_state

# 打印训练后的 Q 表
for state in Q:
    print(f"State {state}: {Q[state]}")